6.2. Постановка задачи синтеза одноканальных систем
Обсудим содержание задачи синтеза для одноканального объекта, представленного на рис. 6.2, где пунктиром выделен датчик. Его поведение описывает передаточная функция
(6.3)
причем
ресурс управления объекта ограничен,
Влияние окружающей среды отражает
возмущающее воздействие
,
а выходная переменная измеряется
датчиком (первичным измерительным
преобразователем, сенсором) с помехой
измерения
так что
где
–
измеренное значение выходной переменой
у.
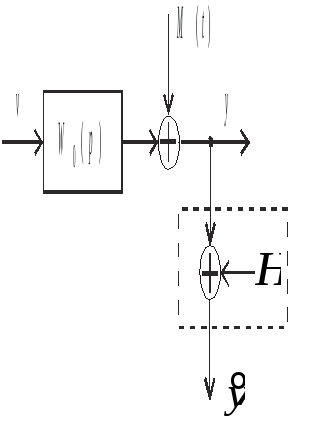
Рис. 6.2. Структурная схема одноканального объекта
Целью
функционирования замкнутой системы
регулирования является обеспечение с
заданной точностью
свойства
.
(6.4)
Наряду с условием статики (6.4) предъявляются требования и к динамике системы, т. е. характеру переходных процессов. Обычно они задаются в виде следующих оценок:
и
(6.5)
выполнение которых представляет собой основную сложность расчета.
Необходимо определить структуру и параметры регулятора, обеспечивающего выполнение требований (6.4) и (6.5) в условиях действия возмущений и помех измерения.
Заметим,
что переменной, которую можно использовать
для организации управляющего воздействия
в системе, является полученная с помощью
датчика оценка выходной величины
.
Поэтому в лучшем случае в системе с
заданной точностью можно обеспечить
выполнение свойства
а не условия (6.4). Для уменьшения влияния помехи при выборе измерительного устройства следует придерживаться рекомендаций:
-
датчик должен обладать значительно большей точностью, чем требуемая точность системы в целом;
-
нужно отфильтровывать помеху, частотный состав которой отличается от рабочих частот системы.
В соответствии с принципом суперпозиции ошибка регулирования в замкнутой системе будет представлять собой сумму трех составляющих
Одна
из них
порожденная входным воздействием,
может быть легко скомпенсирована
масштабированием (см. разд. 3).
Поскольку
помеха измерения
обычно представляет собой высокочастотный
сигнал, ее наибольшее влияние проявляется
в динамике.
Следовательно,
рассчитывать регулятор необходимо
таким
образом, чтобы в системе
управления статическая ошибка,
порожденная возмущением, не превышала
заданного значения
6.3. Условия разрешимости задачи синтеза
Прежде чем выбирать подходящий метод расчета, необходимо убедиться в том, что задача синтеза будет разрешима. С этой целью необходимо исследовать свойства объекта управления и требования, которые предъявляются к качеству работы замкнутой системы. На их основе можно сформировать желаемую передаточную функцию
(6.6)
и определить условия разрешимости задачи синтеза.
6.3.1. Ресурсное ограничение
Рассмотрим объект управления (6.3), полагая, что помеху измерения удалось исключить. В этом случае его операторное уравнение имеет вид
(6.7)
желаемое уравнение для замкнутой системы, соответствующее (6.6), запишем как
(6.8)
Приравнивая правые части выражений (6.7) и (6.8), определим «точное» управляющее воздействие
(6.9)
Если удастся реализовать закон управления (6.9), то поведение замкнутой системы будет точно соответствовать желаемой передаточной функции (6.6).
Поскольку для реального объекта ресурс управления всегда ограничен, задача синтеза будет разрешима при выполнении условия
(6.10)
которое и называется ресурсным ограничением.
К
сожалению, на практике реализовать
управление (6.9) невозможно, так как закон
изменения возмущения
неизвестен, кроме границ его изменения,
которые и следует подставить для
проверки в соотношение (6.10).