6.5.6. Процедура синтеза регулятора модальным методом

На основе рассмотренной операторной методики модального метода синтеза можно предложить следующую процедуру расчета регулятора.

1. Проверяются условия разрешимости задачи синтеза для исходного объекта управления.

2. Записывается передаточная функция корректора статики .

3. Выбирается передаточная функция корректора динамики , где – полином числителя передаточной функции объекта; n – порядок объекта; , – коэффициенты регулятора, численные значения которых должны быть определены в процессе синтеза .

4. В соответствии с расчетной структурной схемой (см. рис. 6.13) находится действительное характеристическое уравнение системы, содержащее неизвестные параметры регулятора (6.52).

5. С учетом требований к качеству переходных процессов ( и ) формируется желаемое характеристическое уравнение системы ()-го порядка в виде (6.56).

6. Приравниваются коэффициенты при соответствующих степенях оператора p желаемого (6.56) и действительного (6.52) характеристических уравнений системы, записываются расчетные соотношения для параметров регулятора (6.57).

7. В случае, когда степени полиномов числителя и знаменателя передаточной функции объекта связаны соотношением , передаточная функция корректора динамики содержит в числителе и знаменателе полиномы одного порядка. Такой регулятор может быть непосредственно реализован в виде цепочки интеграторов с прямыми и обратными связями (п. 3.6.1).

8. В ситуации, когда , корректор динамики представляет собой форсирующее звено, для его реализации в систему следует вводить специальный фильтр (см. рис. 6.16).

9. При расчете стабилизирующей добавки используется методика модального метода синтеза. Сначала формируется желаемое характеристическое уравнение фильтра так, чтобы процессы в нем заканчивались на порядок быстрее, чем в системе (т. е. ). Приравниваются коэффициенты при соответствующих степенях оператора p полученного желаемого и действительного (6.59) характеристических уравнений фильтра, записываются соотношения для расчета параметров стабилизирующей добавки.

10. Параллельная модель и стабилизирующая добавка реализуются в виде цепочки интеграторов, из внутренних переменных модели формируется форсирующий регулятор.

Пример 6.9

Предложить схемную реализацию регулятора, рассчитанного для объекта с передаточной функцией

из примера 6.8.

Найденные из условия требуемого качества процессов в замкнутой системе передаточные функции регулятора имеют вид

,

где

Как видим, корректор динамики представляет собой форсирующее звено первого порядка, поэтому для его реализации введем в систему стабилизирующую добавку с передаточной функцией

.

С учетом передаточной функции модели объекта

запишем действительное характеристическое уравнение фильтра (6.59) в виде

или

.

Представим это уравнение в стандартной форме

Сформируем желаемое характеристическое уравнение фильтра так, чтобы процессы в нем заканчивались на порядок быстрее, чем в системе. При этом выберем

Поскольку в системе не допускается перерегулирование, сохраним это условие и для фильтра. Таким образом, корни должны быть вещественными и располагаться на расстоянии не ближе от мнимой оси. В результате выберем следующие корни:

Запишем желаемое характеристическое уравнение фильтра

В результате подстановки численных значений корней получим

Определим расчетные соотношения для параметров стабилизирующей добавки, для чего приравняем коэффициенты уравнений и :

Отсюда найдем .

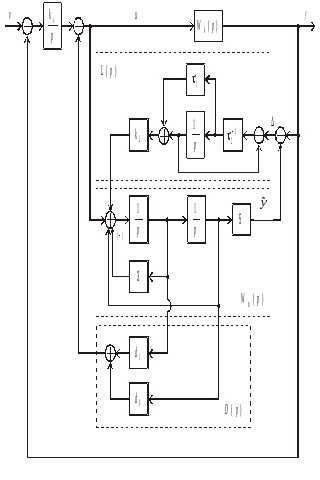Рис. 6.22. Структурная схема системы для примера 6.9

Таким образом, передаточная функция стабилизирующей добавки имеет вид

.

В соответствии с рекомендациями п. 3.6.1 и структурной схемой, представленной на рис. 6.21, приведем на рис. 6.22 полную структурную схему системы с учетом реализации регулятора. На схеме пунктиром выделены: – параллельная модель; – стабилизирующая добавка; – полином числителя корректора динамики.