59.Идея метода гармонической линеаризации нелинейностей

Метод гармонической линеаризации применяется при исследовании устойчивости автоколебаний для линейных систем любого порядка.

Решаются следующие задачи:

1)исследование отсутствия автоколебаний в нелинейных замкнутых системах

2)исследование автоколебаний в НЗС

Пусть имеется нелинейное замкнутое звено

x=a sinwt (1)

(2)

(3)

(4)

(5)

В основе метода гармонической линеаризации лежит представление некоторых нелинейных периодических функций в виде (2) при этом во внимание принимают лишь первые гармоники:

(6)

W_лч(s)=Q(s)/R(s) (7)

Чтобы воспользоваться методом необходимо, чтобы (7) имело свойства фильтра.

|W_лч(jw)|>>|W_лч(jnw)|, n=2,3,… (8)

n[R(s)]>m[Q(s)] (порядок R(s)>порядок Q(s))

lim|W_лч(jw)|=0

(6)→W_н(s)=y(s)/x(s)=q(aw)+q’(aw)s/w (9)

q,q’ – коэффициенты гармонической линеаризации

A₀=0

y= q(aw)+q’(aw)s/w (10)

sinwt=x/a

coswt=sx/aw

q(a,w)=B₁/a

q’(a,w)=A₁/a

29.Анализ устойчивости по логарифмическим частотным характеристикам

А)если разомкнутая функция системы устойчива или нейтральна, то для устойчивости необходимо, чтобы система не охватывала точку (-1;j0).

L(w)=20lg|W(jw)|<0 при φ=-180º

Точка пересечения φ(w) с линией -180º должна лежать перевес частоты среза, левее этой точки может быть лишь четкое пересечение φ с линией -180º.

∆L(w) – запас устойчивости по амплитуде

∆φ(w) - запас устойчивости по фазе

б)в нейтральном состоянии:

в)в неустойчивом состоянии: разность между числом положительных и отрицательных переходов фазовой характеристики φ(w) через -180º левее частоты среза должно равняться l/2 раз.

30.Понятие запасов устойчивости по модулю и по фазе

Для определения устойчивости по критерию Найквиста можно строить не амплитудно-фазовую характеристику, а логарифмическую амплитудную частотную характеристику (ЛАХ) и логарифмическую фазовую частотную характеристику (ЛФХ) разомкнутой системы.

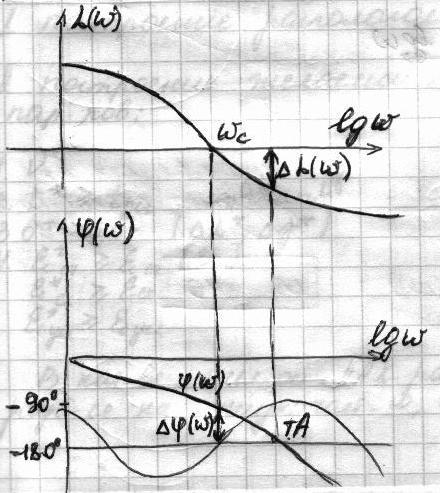
∆L(w) – запас устойчивости по амплитуде

∆φ(w) - запас устойчивости по фазе