
Международный Университет
Бизнеса и Управления
БАЛАКОВСКИЙ
ИНСТИТУТ
БИЗНЕСА И УПРАВЛЕНИЯ
ПРАКТИЧЕСКАЯ РАБОТА
«ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ»
Методическое пособие к практическим работам по курсу: «Теория автоматического управления»
для студентов специальностей 210100 – «Управление и информатика в технических системах»
230700 – «Сервис», 351400 – «Прикладная информатика»,
Одобрено
Редакционно-издательским
советом
Балаковского Института
Бизнеса и Управления
Балаково 2004
ЦЕЛЬ РАБОТЫ: научиться преобразовывать структурные схемы САУ.
Теоритические положения
Для математического анализа динамики системы автоматического управления (САУ) ее обычно изображают в виде схемы, в которой для каждого элемента схемы записывают уравнение прохождения сигнала в виде передаточной функции (ПФ). Для получения ПФ всей системы проводят структурные преобразования и полученная таким образом ПФ является математической моделью всей системы, наиболее удобная для проведения анализа САУ.
Структурная схема автоматического управления отражает прохождение и преобразование сигналов в звеньях системы управления. Она составляется па основе функциональной схемы, причём отдельные звенья структурной схемы могут не соответствовать конструктивным элементам функциональной схемы. Цель преобразования при составлении структурной схемы - получить зависимость выходного сигнала от входного для всей системы через передаточные функции отдельных звеньев системы. [1,8]
Правила структурных преобразовании
При последовательном соединении звеньев САУ, общая передаточная функция равна произведению передаточных функции последовательно соединённых звеньев. (Рисунок 1)
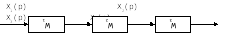
Wобщ = W1 W2 W3
Рисунок 1- Структурная схема последовательно соединенных звеньев
При параллельном соединении звеньев СЛУ общая передаточная функция равна алгебраической сумме передаточных функций параллельно соединенных звеньев. (Рисунок 2)
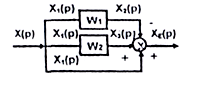
![]()
Рисунок 1.2 - Структурная схема параллельно соединенных звеньев
При получении общей передаточной функции каждая составляющая входит с тем же знаком с каким в сумматор входит ее выходная величина. Так Х2(р) входит в сумматор со знаком (-), поэтому W1 имеет знак (-).
Если какой - то сигнал показан без указания вида передаточной функции то он алгебраически суммируется в виде единицы. Так W3 = +1 Если звено включено в обратную связь, т.е. сигнал этого звена имеет противоположное направление относительно запаса главной цепи, то общая передаточная функция имеет вид дроби (Рисунок 3)

Рисунок 1.3 – Структурная схема звена охваченного обратной связью
Если сигнал обратной связи (Х2(р))суммируется со знаком ( -), то в знаменателе формулы общей передаточной функции ставится знак (+')
Если сигнал обратной связи единичный (т.е. W2=1), то общая передаточная функция имеет вид
![]()
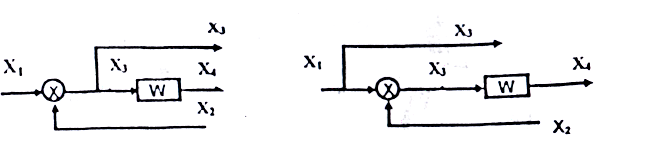
а) Исходная схема 6) Преобразованная схема
Рисунок 4 - Неправильное преобразование сумматора и узла разветвления в структурной схеме.
Правила переноса сумматора или узла разветвления в другую точку схемы
При переносе сумматора по направлению основного сигнала перенесённый сигнал умножается на передаточные функции звеньев, через которые перенесен сигнал. (Рисунок 5)
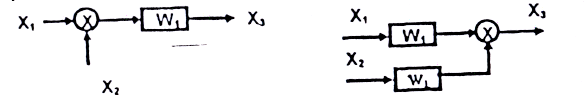
а) Исходная схема б) Преобразованная схема
Рисунок 5 - Перенос сумматора по направлению движения сигнала в структурной схеме.
При переносе сумматора обратно движению основного сигнала, перенесенный сигнал умножается на обратные величины передаточных функций звеньев, через которые перенесен сигнал. (Рисунок 6)
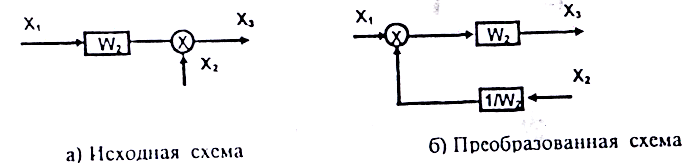
Рисунок 6 - Перенос сумматора обратно направления движения основного сигнала в структурной схеме.
При переносе узлов разветвления по движению основного сигнала, перенесенный сигнал умножается на обратные величины передаточных функций, через которые перенесен сигнал. (Рисунок 7)
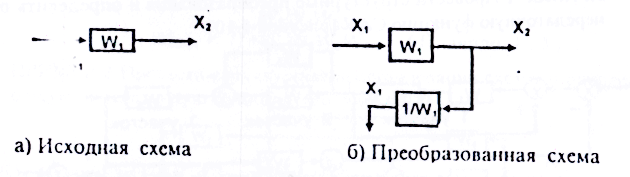
Рисунок 7 - Перенос узлов разветвления по направлению основного сигнала
При перенос узлов разветвления против движения основного сигнала, перенесенный сигнал умножается на передаточные функции, через которые перенесен сигнал. (Рисунок 8)
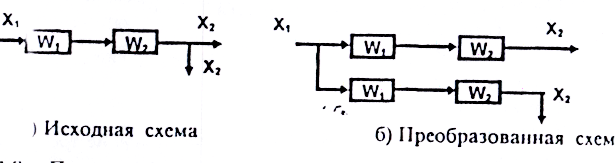
Рисунок 1.9 - Перенос
узлов разветвления против направления
основного
