экзамен / задачи / ЗАДАЧИ

Задача №52

Построить амплитудно-фазовую характеристику апериодического звена с передаточной функцией .

Решение

Передаточная функция звена имеет вид: , следовательно, его частотная функция равна: . Для выделения действительной и мнимой части функции умножим числитель и

знаменатель на комплексно-сопряжённое знаменателю число:

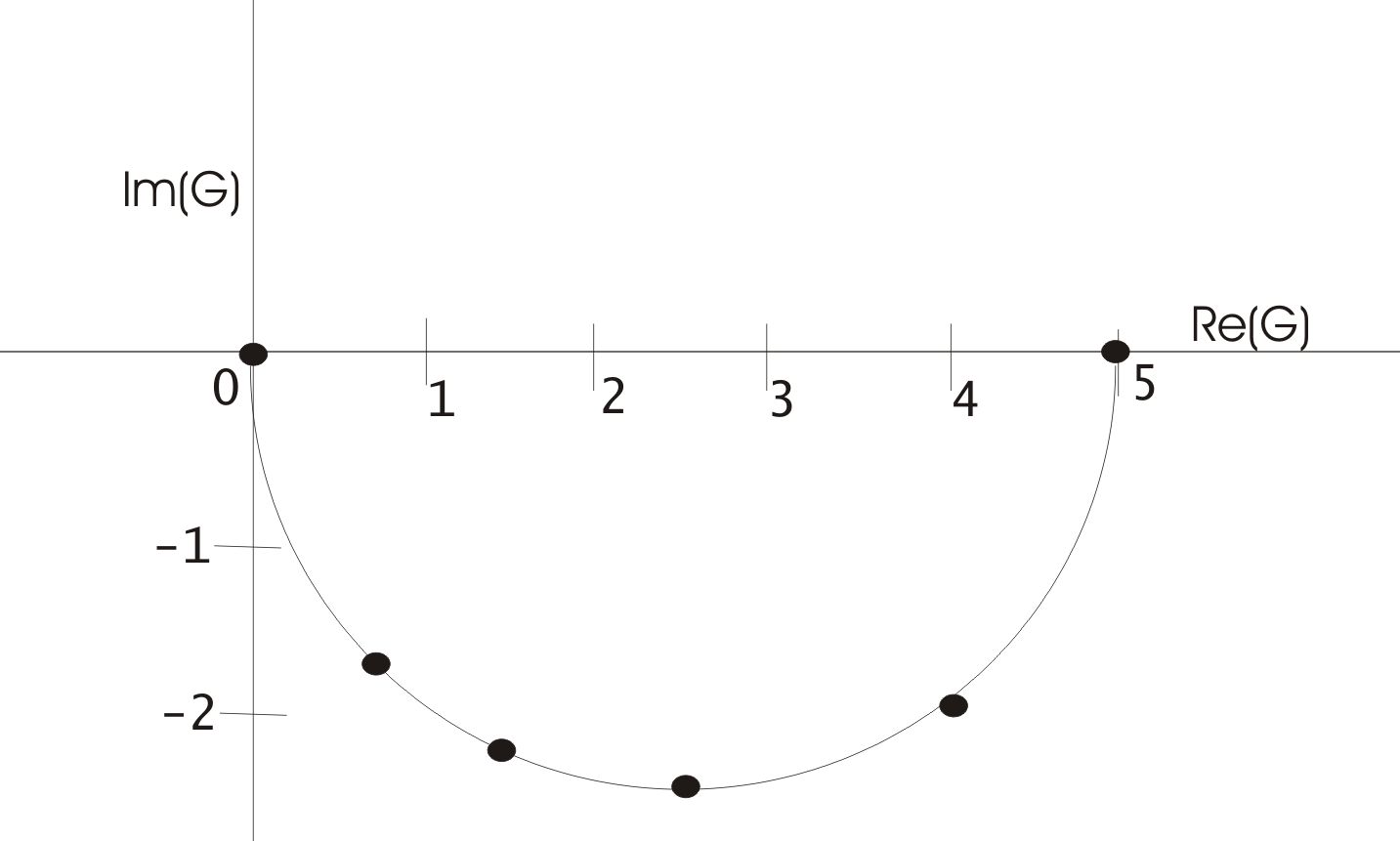
Далее, на комплексной плоскости, по точкам строим амплитудно-фазовую характеристику.

	=0	=5 сек-1	=10 сек-1	=15 сек-1	=25 сек-1	=
Re(G)	5	4	2,5	1,5	0,69	0
Im(G)	0	-2	-2,5	-2,3	-1,72	0

Ответ: гадограф звена с передаточной функцией представлен на рисунке:

Задача №106

Передаточная функция разомкнутой системы имеет вид , где K=5 – общий коэффициент разомкнутой системы, Т=0,5 сек – постоянная времени. Определить устойчивость замкнутой системы.

Решение

для замкнутой системы:

Характеристическое уравнение:

По критерию Рауса-Гурвица имеем:

Знак в первом столбце не меняется, значит, корни в правой полуплоскости отсутствуют, и система устойчива.

Ответ: система устойчива.

Задача №88

Построить логарифмические амплитудную и фазовую характеристики системы с передаточной функцией при К=0,0645 сек; T1=30 мсек; Т2=7 мсек; =0,2.

Решение

Диаграмма Боде для передаточной функции G(s), содержащей несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю.

Для удобства построения передаточную функцию G(s) приведем к виду

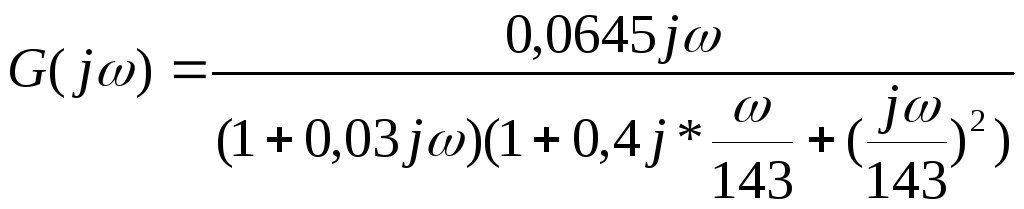
Данная передаточная функция содержит:

1. Постоянный коэффициент усиления К=0,0645;

2. Нуль в начале координат;

3. Полюс при =33,3;

4. Пара комплексно сопряжённых полюсов при 143

Первоначально, необходимо определить как выглядят амплитудные характеристики, соответствующему каждому отдельному элементу:

1. Коэффициенту усиления соответствует логарифмическая амплитудная характеристика 20lg0,0645=-23,8 которая на диаграмме Боде изображается просто в виде горизонтальной линии.

2. Амплитудная характеристика, соответствующая нулю в начале координат, изображается прямой с наклоном +20дБ.

3. Амплитудная характеристика, соответствующая полюсу при =33,3, изображается двумя асимптотами. Высокочастотная асимптота справа от точки излома =33,3 имеет наклон –20дБ, а низкочастотная (слева от точки излома) проходит на уровне 0дБ.

4. Точка излома асимптот соответствующих двум комплексным полюсам будет на частоте 143, наклон высокочастотной асимптоты составит –40дБ (т.к. в сомножителе имеется квадратичный член). Точная ЛАХ определяется коэффициентом затухания =0,2, поэтому в построение обычно вносят поправку исходя из справочных данных.

Результирующая асимптотичная амплитудная характеристика строится путём суммирования асимптот, соответствующих каждому сомножителю передаточной функции. Таким образом прямая с наклоном +20дБ/дек, соответствующая нулю в начале координат, пресекает уровень –23,8 дБ при =1. Далее при =33,3 наклон изменятся на –20дБ/дек, и становится равным нулю (в точной амплитудной характеристики это состояние практически отсутствует). Максимальное значение амплитудной характеристики Мр, для пары комплексных корней зависит от коэффициента затухания , и определяется по формуле: дБ. При =143, что соответствует двум комплексным полюсам, наклон становит равным –40дБ/дек.

Фазовая частотная характеристика также строится путем суммированию соответствующих кривых для каждого отдельного сомножителя:

1. Т.к. постоянный коэффициент усиления является отрицательным, то ему соответствует сдвиг по фазе на -180 .

2. Нулю в начале координат соответствует сдвиг +90.

3. Для полюса при =33,3, до частоты =33,3 фазовый сдвиг отсутствует, а при достижении этой частоты фазовый сдвиг составляет -45.

4. Фазовая характеристика, соответствующая паре комплексных полюсов имеет вид сложной кривой и заимствована из справочных данных.

Логарифмическая амплитудная (точная и неточная - обозначена пунктирной линией) и фазовая характеристики приведены на рисунках:

З-6.14.

Система имеет характеристическое уравнение

q(S)=S⁴+9S³+45S²+87S+50=0

(а) Определите, устойчива ли система, воспользовавшись критерием Рауса-Гурвица.

(б) Найдите корни характеристического уравнения.

Решение:

S⁴ 1 45 50

S³ 9 87 0

S² a 50

S¹ b

S⁰ 50

a=;

b=;

Система устойчива, т.к. все коэффициенты >0.

Решим методом подбора: т.к. все коэффициенты >0,

При S=-1; q(S)=1-9+45-87+50=0, т.е. – 1 – является корнем уравнения;

При S=-2; q(S)=16-8*9+45*4-2*87+50=0, т.е. – 2 – тоже корень уравнения.

(S+1)(S+2)=(S²+3S+2);

S⁴+9S³+45S²+87S+50=(S⁴+3S³+2S²)+(6S³+18S²+12S)+(25S²+75S+50)=(S²+6S+25)(S²+3S+2)=(S+1)(S+2)(S²+6S+25)=(S+1)(S+2)((S+3)²+16)=(S+1)(S+2)(S+3+4i)(S+3-4i)

З-2.18.

Передаточная функция системы имеет вид:

Оприделите y(t), если r(t) имеет вид единичной ступенчатой функции.

Ответ: y(t)=1,33+1,67e^-3t-3e^-5t

Решение:

Т.к. R(t)=1(t), то R(S)=, т.к. 1(t)=;

Y(S)=G(S)R(S)=;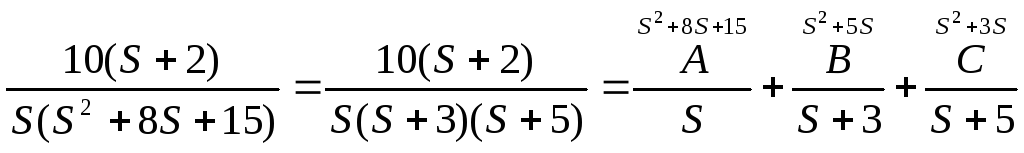

т.к. A=4/3 то,

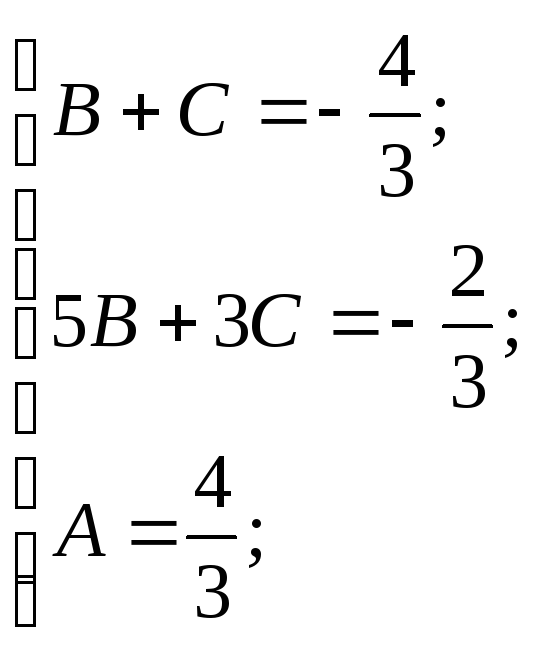
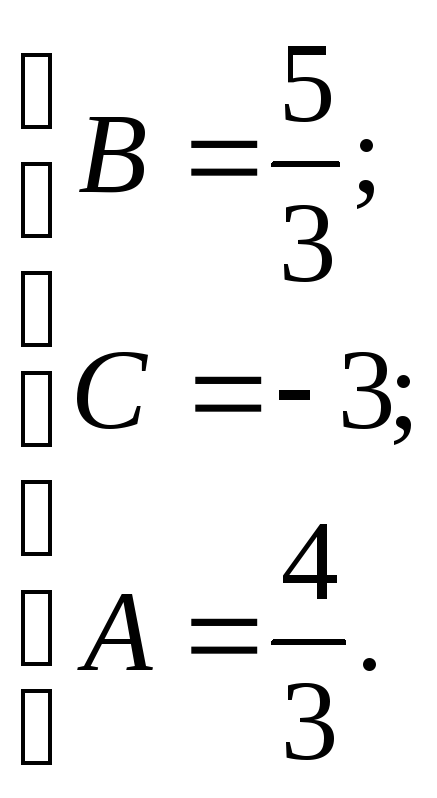
Тогда Y(S)=

Y(t)=L^-1(Y(S))=, т.к. e^-at= .