
РГР / устойчивость нелинейной систем / ЮРА_РГР2
.doc
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
КАФЕДРА УИТ
Расчетно-графическая работа №2
по дисциплине
Теория автоматического управления
Исследование устойчивости нелинейных систем автоматического управления
Выполнил ст. гр. УИТ-41
Удалов Ю.В.
Принял доцент каф. УИТ
Скоробогатова Т.Н. _______
“______” ___________2003
2003
СОДЕРЖАНИЕ
1 Техническое задание 3
2 Упрощение структурной схемы 3
3 Построение фазового портрета 5
4 Анализ устойчивости 6
Вариант № 44
1 Техническое задание
Задана система автоматического регулирования (рисунок 1) с наличием нелинейного элемента.
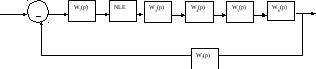
Рисунок 1
W1(p)=![]() ;
;
W3(p)=![]() ;
;
W4(p)=0,1;
W5(p)= 203;
W6(p)=
![]() .
.
W7(p)=0,12
График, описывающий нелинейный элемент NLE приведен на рис. 2
 y
y


 20
20

 -2
0
-2
0
2 x
 -20
-20
Рисунок 2
2 Упрощение структурной схемы
Разорвем цепь перед нелинейным элементом и получим схему (рисунок 3)

Рисунок 3
В цепи рисунка 4 можно четко выделить линейную и нелинейную части, преобразуем (рисунок 3).

Рисунок 4
Обозначения: W8(р)= W1(p)·W7(p)· W3(p)·W4(p)·W5(p)·W6(p)
![]()
![]()
3 Построение фазового портрета
Передаточную
функцию можно записать в виде
![]() или
или
![]() ,
подставляя в эту формулу значение
передаточной функции получим:
,
подставляя в эту формулу значение
передаточной функции получим:
![]()
Приведенную формулу можно записать в виде:
![]()
Воспользуемся пакетом MathCad для решения этого дифференциального уравнения.
Введем замену pix=yi и исключим из правой части уравнения производную
Получим систему уравнений для участков (-∞;-2), (-2;2) и (2;+∞):

Создадим матрицу для решения дифференциального уравнения:

В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицу начальных условий:
![]()
Возьмем количество
точек равным 1000 и конечное время
интегрирования 100, то матрица решений
запишется как:
![]() .
.
По введенным данным получим фазовый портрет (рисунок 5).

Рисунок 5
4 Анализ устойчивости
На рисунке 5 представлен фазовый портрет нелинейной системы. Это типовой вид кривой. До перехода через точку -2 работает первое уравнение системы, при переходе через эту точку начинает работать второе уравнение. Третье уравнение работает при переходе через точку 2. Характер фазовой линии такой, что она постоянно приближается к началу координат, т.е. нелинейная система с релейным элементом устойчива. При движении к состоянию устойчивости амплитуда колебаний постоянно уменьшается, а частота переключения растет. Получаем, что амплитуда колебаний в итоге примет нулевое значение, а частота колебаний станет бесконечно большой.
