Задание для контрольной работы

По данным своего варианта, представленным в таблице, необходимо:

1. Придумать признак, которым могут обладать элементы данной совокупности.

2. Построить интервальный ряд распределения (взять число частичных интервалов не менее 7).

3. Построить гистограмму и кумуляту относительных частот.

4. Вычислить выборочные характеристики статистического распределения (выборочную среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс). Проанализировать полученные результаты.

5. С помощью критериев Колмогорова и Пирсона проверить гипотезу о нормальном распределении признака Х генеральной совокупности.

6. Если в п.6 получилось, что признак Х имеет нормальный закон распределения, то найти интервальную оценку при доверительной вероятности 0,95.

Образец выполнения контрольной работы

Имеются выборочные данные о норме расхода материала на изготовление одной единицы продукции, кг

95,08	83,52	85,74	80,43	85,63	61,41	85,87	71,94	89,25
89,14	84,73	85,00	105,80	87,87	85,73	108,75	80,08	102,24
92,52	84,69	95,39	86,63	78,85	74,64	89,80	76,00	110,03
82,97	79,81	71,51	91,11	85,52	94,09	80,00	83,40	90,76
90,31	112,09	69,66	69,27	60,58	101,09	115,09	82,89	75,77
95,12	85,01	69,39	99,23	96,32	83,35	79,38	97,48	91,47
93,02	73,12	94,02	85,61	90,91	91,59	88,96	84,26	71,73
74,41	93,64	88,29	87,33	89,31	65,51	84,44	76,50	75,81
83,52	58,61	77,50	90,61	99,65	78,72	91,65	98,58	86,63
74,54	93,29	87,25	85,95	83,57	93,81	93,91	112,14	80,22
96,86	102,77	86,68	68,93	89,90	95,11	111,73	106,04	106,19
70,21

Таблица 4. Исходные статистические данные

Решение.

ЗАДАНИЕ 1. Признак Х – норма расхода материала на изготовление одной единицы продукции, кг

ЗАДАНИЕ 2. Составим интервальный ряд распределения для табл. 4. Пусть число частичных интервалов k = 8, , . Тогда по формуле (1.2) получим

.

Получившийся интервальный ряд представлен во втором столбце табл. 5.

ЗАДАНИЕ 3. Построим гистограмму и кумуляту относительных частот для табл. 5. Все необходимые вычисления сведем в столбцы (4), (5) и (6) таблицы 5:

№
1	2	3	4	5	6
1 2 3 4 5 6 7 8	58,61-65,67 65,67-72,73 72,73-79,79 79,79-86,85 86,85-93,91 93,91-100.97 100,97-108,03 108,03-115,09	4 8 12 28 24 12 7 5	0,0057 0,0113 0,0170 0,0397 0,0340 0,0170 0,0099 0,0071	4 12 24 52 76 88 95 100	0,04 0,12 0,24 0,52 0,76 0,88 0,95 1
	-	100	-	-	-

Таблица 5.

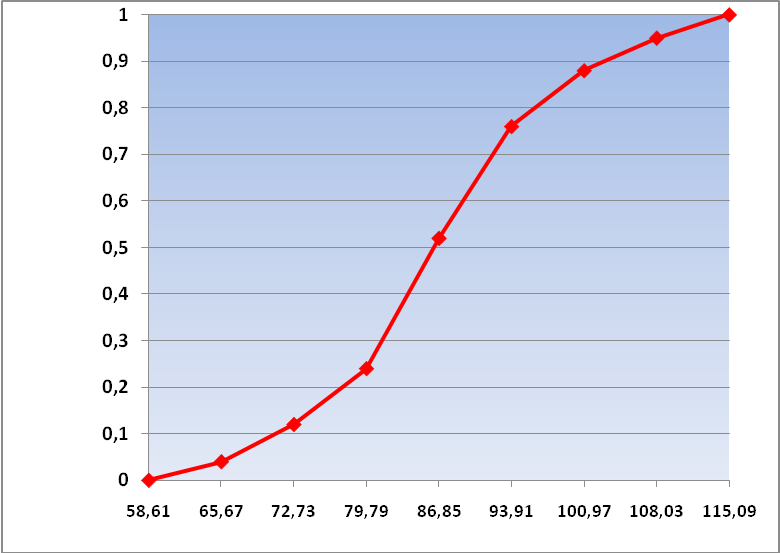
Рисунок 8. Кумулята относительных частот

Рисунок 9. Гистограмма относительных частот

ЗАДАНИЕ 4. Вычислим выборочные характеристики распределения нормы расхода материала на изготовление одной единицы продукции, кг (таблица 5)

Распределение задано интервальным рядом. Поэтому, прежде, чем вычислять характеристики, нужно заменить интервальный ряд дискретным. Для этого каждый интервал заменим его серединой . Все необходимые вычисления сведем в (7), (8) и (9) столбцы таблицы 5:

№
1	2	3	7	8	9	10
1 2 3 4 5 6 7 8	58,61-65,67 65,67-72,73 72,73-79,79 79,79-86,85 86,85-93,91 93,91-100.97 100,97-108,03 108,03-115,09	4 8 12 28 24 12 7 5	62,14 69,2 76,26 83,32 90,38 97,44 104,5 111,56	248,56 553,6 915,12 2332,96 2169,12 1169,28 731,5 557,8	2428,4001 2472,2824 1327,8933 335,0886 311,1437 1363,7807 2198,1377 3070,3907	15445,52 38309,12 69787,05 194382,2 196045,1 113934,6 76441,75 62228,17
∑	-	100	-	8677,94	13507,117	766573,5

Таблица 5. (Продолжение)

4.1 Выборочная средняя характеризует типичное для выборки значение признака. Т.к. данные сгруппированы, то (взвешенная средняя арифметическая).

(кг) – средняя норма расхода материала на изготовление единицы продукции.

4.2. Мода - это значение признака, которому соответствует наибольшая частота (наиболее часто встречающееся значение признака Х).

(кг) т.к. .

4.3. Медиана - это значение признака, делящее ранжированный вариационный ряд на две равные по численности группы.

Т.к. n=100 – четное число, то (кг).

Т.к. в результате вычислений , то распределение признака Х асимметричное.

4.4. Размах вариации (кг).

4.5. Дисперсия - это выборочная средняя арифметическая квадратов отклонений значений признака Х от выборочной средней , то есть

Рассчитаем выборочную дисперсию двумя способами:

4.5.1. , (см. столбец 9 таблицы);

4.5.2.

,

где (см. столбец 10 таблицы).

4.6. Выборочное среднее квадратическое отклонение есть арифметический квадратный корень из дисперсии

(кг) – в среднем норма расхода материала на изготовление изделия отклоняется от её среднего значения на 11,62 кг.

4.7. Коэффициент вариации .

Т.к. < 33%, то рассматриваемая выборочная совокупность однородная.

4.8. Коэффициент асимметрии вариационного ряда рассчитывается по формуле

.

(см. столбец 11 таблицы 5)

Т.к. А>0, то имеет место положительная (правосторонняя) асимметрия.

4.9. Эксцессом вариационного ряда называется число

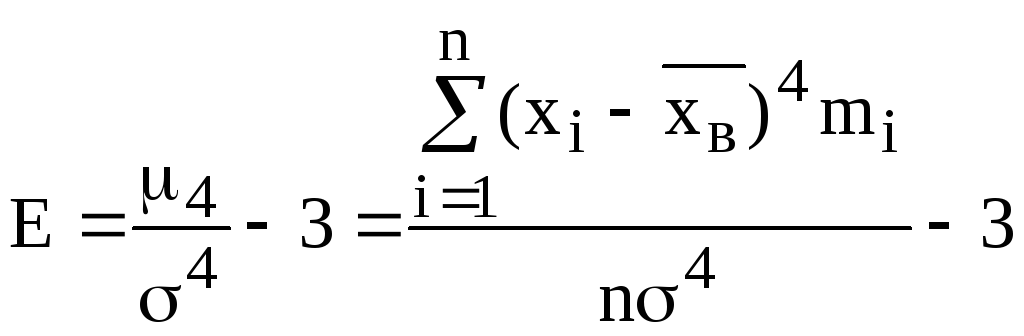
(см. столбец 12 таблицы)

Эксцесс является показателем “крутости” вариационного ряда по сравнению с нормальным распределением. Т.к Е<0, то полигон вариационного ряда имеет более пологую вершину по сравнению с нормальной кривой.

№
1	2	3	7	11	12
1 2 3 4 5 6 7 8	58,61-65,67 65,67-72,73 72,73-79,79 79,79-86,85 86,85-93,91 93,91-100.97 100,97-108,03 108,03-115,09	4 8 12 28 24 12 7 5	62,14 69,2 76,26 83,32 90,38 97,44 104,5 111,56	-59834,322 -43461,242 -13968,641 -1159,2053 1120,30097 14538,7206 38952,318 76086,1233	1474281,8 764022,55 146941,72 4010,155 4033,7665 154991,49 690258,45 1885459,8
∑	-	100	-	12274,0557	5123999,7

Таблица 5. (Продолжение)

ЗАДАНИЕ 5. С помощью критерия Колмогорова проверим гипотезу о нормальном распределении признака Х генеральной совокупности.

: Признак Х генеральной совокупности имеет нормальный закон распределения;

: Признак Х генеральной совокупности имеет закон распределения, отличный от нормального.

Зададим =0,05.

В критерии Колмогорова в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривается максимальное значение абсолютной величины разности между эмпирической функцией распределения и соответствующей теоретической функцией распределения

,

называемое статистикой критерия Колмогорова.

Для расчета значения D прежде всего нужно знать параметры a и , также нужно иметь таблицу значений эмпирической функции и таблицу значений теоретической функции . Параметры распределения были определены ранее (п. 3.1 и 3.6) a, . Значения эмпирической функции распределения также были найдены ранее (столбец (6) таблицы 2). Столбец (17) заполняется по формуле

.

Например, для х=65,67

Остальные расчеты представим в продолжение таблицы 5.

Правая граница интервала
13	14	15	16	17	18
65,67 72,73 79,79 86,85 93,91 100,97 108,03 115,09	0,04 0,12 0,24 0,52 0,76 0,88 0,95 1	-1,82 -1,21 -0,60 0,01 0,61 1,22 1,83 2,44	-0,4656 -0,3869 -0,2257 0,0040 0,2291 0,3883 0,4664 0,4927	0,0344 0,1131 0,2743 0,504 0,7291 0,8883 0,9664 0,9927	0,0056 0,0069 0,0343 0,0160 0,0309 0,0083 0,0164 0,0073

Таблица 5. (Продолжение)

Из столбца (18) таблицы 2 имеем . Тогда

При уровне значимости =0,05 , из таблицы 2 найдём соответствующее критическое значение

Вывод: так как , то нет оснований отвергать нулевую гипотезу о том, что признак Х генеральной совокупности имеет нормальный закон распределения. Расхождение между значениями и случайно.

Проверим гипотезу о нормальном распределении признака Х генеральной совокупности с помощью критерия Пирсона.

: Признак Х генеральной совокупности имеет нормальный закон распределения;

: Признак Х генеральной совокупности имеет закон распределения, отличный от нормального.

Зададим =0,05.

Для проверки гипотезы используется случайная величина

,

имеющая распределение (хи-квадрат) с k=S-r-1 степенями свободы, где S – число частичных интервалов в случае интервального ряда и число различных значений в случае дискретного ряда, r – число параметров проверяемого распределения. Так как для нормального распределения r=2, число степеней свободы k = S-3.

Для интервального ряда теоретическая частота , в случае проверки гипотезы о нормальном распределении, вычисляется по формуле

,

где Ф(t) – функция Лапласа, а и - оценки параметров предполагаемого нормального распределения.

Для применения критерия Пирсона необходимо, чтобы в каждом интервале было не менее 5 наблюдений. В рассматриваемом примере для 1 – го и 8 - го интервалов это условие не выполняется. Следовательно, объединим соседние интервалы, чтобы в них число значений было не менее 5. В этом случае при вычислении числа степеней свободы в качестве величины S берется соответственно уменьшенное число интервалов (S=6).

Все необходимые расчеты представим в продолжение таблицы 2.

Для этого введём обозначения: , .

№
1	2	3	19	20	21	22	23	24	25	26
1 2 3 4 5 6	58,61-72,73 72,73-79,79 79,79-86,85 86,85-93,91 93,91-100,97 100,97-115,09	12 12 28 24 12 12	72,73 79,79 86,85 93,91 100,97 115,09	-1,21 -0,61 0,006 0,61 1,22 2,44	-0.3869 -0,2291 0,0040 0,2291 0,3883 0,4927	58,61 72,73 79,79 86,85 93,91 100,97	-2,42 -1,21 -0,61 0,006 0,61 1,22	-0,4922 -0,3869 -0,2291 0,0040 0,2291 0,3883	11 16 23 19 16 10	0,091 1 1,09 1,32 1 0,4
∑		100							95	4,901

Таблица 5. (Продолжение)

Итак, . (См. приложение 4, [1]).

Вывод: так как , то есть попадает в область принятия гипотезы, следовательно, нет оснований отвергать гипотезу , по выборочным данным признак Х генеральной совокупности имеет нормальный закон распределения. Расхождение между и случайно.

ЗАДАНИЕ 6. Найдём интервальную оценку при доверительной вероятности 0,95.

Интервальную оценку параметра с надежностью 0,95 при неизвестном можно записать следующим образом:

,

где (См. приложение 8, [1]), - исправленное среднее квадратическое отклонение. Итак,

,

.

Таким образом, с надёжностью 0,95 можно утверждать, что норма расхода материала на изготовление одной единицы продукции находится в промежутке от 84,07 кг до 89,49 кг.