
Национальный Технический Университет Украины
«Киевский Политехнический Институт»
Контрольная работа
по курсу «Теория автоматического управления»
тема:
«Линейная САУ «Разомкнутый принцип управления»
Вариант № 1
Приняла: Выполнил:
Польшакова О. М. ст. гр. ЗИК – 71
факультета ИВТ
Алёшкин С.С.
«Киев – 2010»
Линейная САУ «разомкнутый принцип управления»

–
Структурная схема
Задание:
1.Построить математическую модель САУ.
2.Составить дифференциальное уравнение САУ по задающему и возмущающему воздействиям.
3.Определить передаточные функции САУ по входному сигналу G(t) и возмущению Мн(t).
3.1.Определить передаточную функцию по входу от задающего воздействия при равенстве нулю возмущающего воздействия при нулевых начальных условиях.
3.2.Определить передаточную функцию по входу от возмущающего воздействия при равном нулю задающего воздействия при нулевых начальных условиях.
3.3. Определить передаточную функцию по входу от возмущающего воздействия при неравенстве 0 G(t) и при нулевых начальных условиях когда канал компенсации замкнут.
3.4.Определить закон управления.
4.Определить временные характеристики.
4.1.Рассмотреть САУ при МH(t)=0, а входное воздействие G(t)=1(t) – скачок, y(0)=0, а первая производная y'(0)=0.
4.2.Рассчитать и построить переходную функцию.
4.3. Рассчитать функцию веса.
5.Частотные характеристики (рассчитать и построить).
5.1.Амплитудно-фазочастотная характеристика (АФЧХ), когда МН(t)=0.
5.2.Амплитудно-частотную характеристику
5.3.Фазочастотную характеристику
5.4.Логорифмитическая амплитудно-частотная характеристика.
|
Кпе |
Кпр |
Ку |
Ко |
Кр |
Ту |
То |
Bo |
|
1,5 |
2 |
4 |
1 |
0,75 |
0,1 |
0,2 |
1 |
Для удобства, перерисуем схему с передаточными функциями звеньев:
. . Мн(s)
W3
W2
W4
W6
W8













W1


G(s)
Y(s)


W5
W7
где
W1=
Km
; W2=
B0
; W3=
Кпе
; W4=
Кпр
; W5=
 ; W6=
K0
; W7=
; W6=
K0
; W7=
 ; W8=
Kp
; W8=
Kp
общий коэффициент усиления:
K = Кпе* Кпр*Ky* K0* Kp = 9
Преобразуем схему
Мн(s)









W1


W2
A D
W4*W5*W6
W7*W8
W3
G(s)
B
C
Y(s)

1.Построить математическую модель САУ.
Запишем математическую модель системы, когда на нее действует задающий, возмущающий сигналы и когда канал компенсации замкнут:
Y(s)
= С-D
= (В*
W4*W5*W6
- Мн(s)*W2)*W7*W8
= [(G(s) * W3+A)
*W4*W5*W6
- Мн(s)*
*W2]*W7*W8
= [(G(s) * W3+МН(s)*
W1 )
*W4*W5*W6
- Мн(s)*
W2]*W7*W8
= = [G(s)*
W3*W4*W5*W6
+ МН(s)*W1*
W4*W5*W6
- Мн(s)*
W2]*W7*W8
=
)
*W4*W5*W6
- Мн(s)*
W2]*W7*W8
= = [G(s)*
W3*W4*W5*W6
+ МН(s)*W1*
W4*W5*W6
- Мн(s)*
W2]*W7*W8
=
=
[G(s) *
 + МН(s)*
(
+ МН(s)*
( - B0)]
*
- B0)]
*
Найдем при каком значении Кm будет полностью компенсироваться возмущающее воздействие:
 -
B0
= 0 => Кm
=
-
B0
= 0 => Кm
=
 =
=
 = 0,125
= 0,125
Т.к. ключ разомкнут, то канал компенсации равен 0, т.е. МН(s)*W1* W4*W5*W6 =0, поэтому далее рассматривается математическая модель при разомкнутом ключе:
Y(s)= G(s)* W3*W4*W5*W6*W7*W8 - Мн(s)* W2*W7*W8
2. Составить дифференциальное уравнение САУ по задающему и возмущающему воздействиям.
Дифференциальное ур-е САУ по задающему воздействию :
где, МН(t)=0 => Мн(s)* W2*W7*W8 = 0 ,
следовательно
Y(s)=
G(s)* W3*W4*W5*W6*W7*W8
=
G(s) *
 ,
,
тогда
(Ту*s+1)*(To*s+1)*Y(s)=G(s)*Кпе*Кпр*Ку*Ко*Кр
(Ту*То*s2 + (Ty+To)*s + 1)*Y(s) =G(s)*Кпе*Кпр*Ку*Ко*Кр
Ту*То*Y(s)*s2 + (Ty+To)*Y(s)*s + Y(s) = G(s)*Кпе*Кпр*Ку*Ко*Кр
Учитывая,
что S
=
 , имеем обратное преобразование
, имеем обратное преобразование
Ту*То*у``(t) + (Ty+To)*y`(t) + y(t) = g(t)*Кпе*Кпр*Ку*Ко*Кр
Подставив значения, получим:
0,02*y``(t) + 0,3*y`(t) + y(t) = 9*g(t)
Дифференциальное ур-е САУ по возмущающему воздействию:
где, g(t)=0 => G(s)* W3*W4*W5*W6*W7*W8 = 0
следовательно
Y(s)
=- Мн(s)*
W2*W7*W8
= -MH(s)
*

тогда
То*Y(s)*s +Y(s) = -MH(s)*Bo*Kp
или
0,2*y`(t) + y(t) = -0,75* MH(t)
3.Определить передаточные функции САУ по входному сигналу G(t) и возмущению Мн(t).
3.1.Определить передаточную функцию по входу от задающего воздействия при равенстве нулю возмущающего воздействия при нулевых начальных условиях.
По условию МН(t)=0
тогда
Y(s)= G(s)* W3*W4*W5*W6*W7*W8
и
передаточная функция по входу от задающего воздействия:
WЗ(s)
=
 = W3*W4*W5*W6*W7*W8
=
= W3*W4*W5*W6*W7*W8
=
 =
=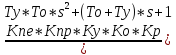 =
=

3.2.Определить передаточную функцию по входу от возмущающего воздействия при равном нулю задающего воздействия при нулевых начальных условиях.
По условию g(t)=0,
тогда
Y(s)= -Мн(s)* W2*W7*W8
и передаточная функция по входу от возмущающего воздействия:
Wвозм
=
 =
=
 =
=

3.3. Определить передаточную функцию по входу от возмущающего воздействия при неравенстве 0 G(t) и при нулевых начальных условиях, когда канал компенсации замкнут.
Рассмотрим схему, когда канал компенсации замкнут:
W2
W4*W5*W6










W1

МН(s)
A D_
W7*W8
W3
G(s)
B C
Y(s)

-
Передаточная функция, когда g(t)=const, Мн(t)=0 и канал разомкнут:
Описано в п.п. 3.1.
-
Передаточная функция, когда g(t)=0, Мн(t)=const и канал разомкнут:
Описано в п.п. 3.2.
-
Передаточная функция, когда g(t)=const, Мн(t)=const и канал разомкнут:
Y(s)=
G(s)* W3*W4*W5*W6*W7*W8
- Мн(s)*
W2*W7*W8
=
 * G(s)
-
* G(s)
-
 *
Мн(s)
=
*
Мн(s)
=
 *
G(s)
*
G(s)
 *
Мн(s)
*
Мн(s)
-
Передаточная функция, когда g(t)=const, Мн(t)=const и канал замкнут:
Y(s) = G(s)* W3*W4*W5*W6*W7*W8 + МН(s)*W1* W4*W5*W6*W7*W8 - МН(s)* W2*W7*W8
=
 *
G(s) +
*
G(s) + *
Мн(s)
*
Мн(s)
 *
Мн(s)
*
Мн(s)
4.Определить временные характеристики.
4.1.Рассмотреть САУ при МH(t)=0, а входное воздействие G(t)=1(t) – скачок, y(0)=0, а первая производная y'(0)=0.
Y(s)=
G(s)* W3*W4*W5*W6*W7*W8
=
G(s) *

(Ту*s+1)*(To*s+1)*Y(s)=G(s)*Кпе*Кпр*Ку*Ко*Кр
(Ту*То*s2 + (Ty+To)*s + 1)*Y(s) =G(s)*Кпе*Кпр*Ку*Ко*Кр
Ту*То*Y(s)*s2 + (Ty+To)*Y(s)*s + Y(s) = G(s)*Кпе*Кпр*Ку*Ко*Кр
Учитывая,
что S
=
 , имеем обратное преобразование
, имеем обратное преобразование
Ту*То*у``(t) + (Ty+To)*y`(t) + y(t) = g(t)*Кпе*Кпр*Ку*Ко*Кр
Подставив значения, получим:
0,02*y``(t) + 0,3*y`(t) + y(t) = 9*g(t)
4.2.Рассчитать и построить переходную функцию.
Исходя из условия п.п. 4.1. МН(t)=0 и g(t)=1(t) , и нулевые начальные условия, то рассмотрим дифференциальное ур-е САУ по задающему воздействию:
0,02*y``(t) + 0,3*y`(t) + y(t) = 9*g(t)
Учитывая,
что S
=
 , а y(t)
, а y(t)
 Y(s)
, g(t)
Y(s)
, g(t)
 G(s)
, то
G(s)
, то
0,02*Y(s)*s2
+ 0,3*Y(s)*s
+ Y(s)
= 9*G(s)
, т.к. g(t)=1(t),
а изображение 1(t)
 и учитывая, что при этом на Y(s)
накладывается обязательство быть
изображением переходной функции,
запишем:
и учитывая, что при этом на Y(s)
накладывается обязательство быть
изображением переходной функции,
запишем:
0,02*H(s)*s2
+ 0,3*H(s)*s + H(s) = 9*
 => H(s) =
=> H(s) =

Для того, чтоб узнать переходную функцию, воспользуемся формулой разложения Карсона – Хевисайда:
h(t)
=
 ,
,
где
С(s) = 9
D`(s)
= ( )`
= 0,06*s2
+ 0,6*s
+ 1
)`
= 0,06*s2
+ 0,6*s
+ 1
Найдем корни хар-ого уравнения:
 =
0
=
0
s1=0 ,
 =
0
=
0
s2=
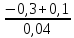 =
=
 ; s3
=
; s3
=
 = -10
= -10
тогда за формулою разложения Карсона – Хевисайда:
h(t)
=
 =
=

h(t)
=

|
t |
h(t) |
|
0 |
0 |
|
1 |
8,879 |
|
2 |
8,999 |
|
3 |
9 |
|
4 |
9 |

График переходной функции
4.3. Рассчитать функцию веса.
Функция веса равна первой производной от переходной функции:
w(t) = h`(t)
тогда,
h`(t)
= 90 *
 - 90 *
- 90 *

следовательно
w(t)
= 90
*
 - 90 *
- 90 *

5.Частотные характеристики (рассчитать и построить).
5.1.Амплитудно-фазочастотная характеристика (АФЧК), когда МН(t)=0.
По условию МН(t)=0, тогда рассматриваем передаточную функцию по задающему воздействию:
WЗ(s)
=

Положим s = j*ω ,
W(j*ω)
=
 =
=
= =
= =
=
 =
=
=

АФЧХ системы:
W(j*ω)
=

Откуда,
U(ω)
= ReW(j*ω)
=
 - действительная
частотная характеристика
- действительная
частотная характеристика
V(ω)
= ImW(j*ω)
=
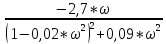 – мнимая
частотная характеристика
– мнимая
частотная характеристика
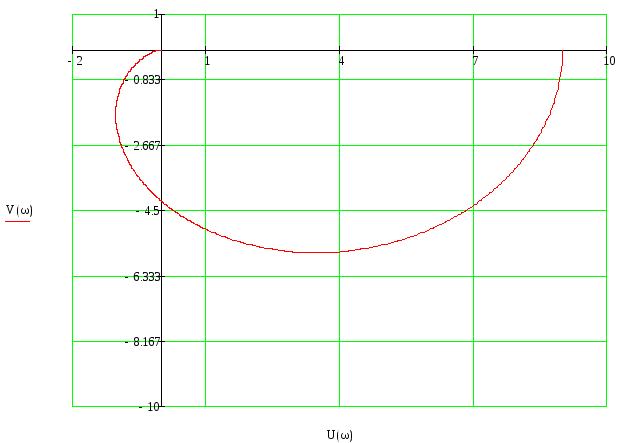
График АФЧХ
5.2.Амплитудно-частотную характеристику
АЧХ системы определяется за формулой:
А(ω)
=

A(ω)
=
 =
=
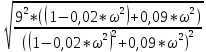
A(ω)
=


График АЧХ
5.3.Фазочастотную характеристику
ФЧХ системы определяется за формулой:
φ(ω)
= arctg ( )
)
φ(ω)
=


График ФЧХ
5.4.Логорифмитическая амплитудно-частотная характеристика
ЛАЧХ определяется за формулой :
L(ω) = 20 * lg(A(ω))
L(ω)
= 20*lg( )
= 20*lg(9) – 10*lg(
)
= 20*lg(9) – 10*lg( )
)
|
ω, с-1 |
L(ω), Дб |
|
0.01 |
19,085 |
|
0.1 |
19,083 |
|
1 |
18,871 |
|
10 |
9,085 |
|
100 |
-26,99 |
|
1000 |
-66,936 |

График ЛАЧХ
