УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БАРАНОВИЧСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

КАФЕДРА ФИЗИКО-МАТЕМАТИЧЕСКИХ ДИСЦИПЛИН

ИНЖЕНЕРНЫЙ ФАКУЛЬТЕТ

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС

для обеспечения

контролируемой самостоятельной работы студентов (КСР)

по учебной дисциплине «Высшая математика»

Для специальности

1-25 01 08 «Бухгалтерский учет, анализ и аудит в агро промышленном комплексе»

1-26 02 03 «Маркетинг»

1-25 01 07 «Экономика и управление на предприятии агропромышленного комплекса»

1-25 01 13 «Экономика и управление туристской индустрией»

1-й курс

Всего КСР — 2 часа, 1 семестр Материалы подготовлены

Лекция — 2 часа Гурской О.В., преподавателем

Кафедры

(в соответствии с Положением о

контролируемой самостоятельной работе

студентов БарГУ, утвержденным

18.08.2009 № 341)

Барановичи 2011

СОДЕРЖАНИЕ

1. Элементы аналитической геометрии в пространстве (2 часа).

ИНФОРМАЦИОННО-МЕТОДИЧЕСКАЯ ЧАСТЬ

ТЕМА: ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В ПРОСТРАНСТВЕ

Цель КСР:

– овладение учебным материалом дисциплины в объеме, требуемом учебной программой;

– формирование навыков самообразования в учебной, научной, производственной и управленческой деятельности;

– развитие учебных способностей, умений, навыков и принятия самостоятельных решений в профессиональной деятельности.

Вопросы для изучения:

1. Основные виды уравнений плоскости в пространстве.

2. Взаимное расположение двух плоскостей.

3. Прямая в пространстве.

4. Взаимное расположение прямых в пространстве.

5. Взаимное расположение прямой и плоскости.

6. Поверхность второго порядка.

Методические указания:

1. Изучите предлагаемые вопросы по литературным источникам и лекции.

2. Составьте краткий конспект.

3. Ответьте на вопросы для самоконтроля.

ТЕМА: ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В ПРОСТРАНСТВЕ

. Плоскость и прямая в пространстве

1. Общее уравнение плоскости.

Пусть дана точка , лежащая в плоскости и ненулевой вектор , перпендикулярный к плоскости и называемый нормальным вектором плоскости

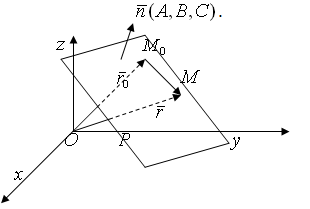
Пусть произвольная точка плоскости . Тогда вектор плоскости ортогонален вектору , т.е.

или

.

Очевидно, условию удовлетворяют координаты тех и только тех точек пространства, которые принадлежат плоскости . Поэтому они являются искомыми уравнениями плоскости, причем называется уравнением плоскости в векторной форме. Уравнение можно привести к виду

,

где . Уравнение называется общим уравнением плоскости с нормальным вектором . Верно и обратное, т.е. любое уравнение вида (1.4.22), где , определяет плоскость с нормальным вектором .

Упражнение. Докажите последнее утверждение.

2. Уравнение плоскости, параллельной двум данным векторам.

Пусть даны два неколлинеарных вектора и , параллельных плоскости , проходящей через данную точку .

Пусть – произвольная точка принадлежащая . Тогда векторы и и компланарны, т.е. их смешанное произведение равно нулю:

или в координатной форме:

.

3. Уравнение плоскости, проходящей через три точки.

Пусть даны три точки , ,, принадлежащие искомой плоскости . Тогда векторы и очевидно, параллельны этой плоскости. Используя уравнение (1.4.24), получим искомое уравнение плоскости

.

4. Нормальное уравнение плоскости. Расстояние от точки до плоскости. Отклонение.

Пусть – единичный вектор нормали к плоскости , проведенный к плоскости из начала координат. Тогда .

Если – произвольная точка плоскости с радиус-вектором , то при любом положении точки на плоскости выполняется , где – длина перпендикуляра , т.е.

.

Переходя к координатной форме записи, получим:

.

Уравнение называется нормальным уравнением плоскости. Если плоскость задана общим уравнением, то разделив обе его части на , где знак перед корнем выбирается противоположным знаку , мы приведем общее уравнение к нормальному виду, т.е. к виду . Множитель называется нормирующим множителем уравнения плоскости.

Пусть есть произвольная точка пространства . Легко видеть, что , где – расстояние от точки до плоскости , а знак перед выбирается в зависимости от того, где находится точка – по одну сторону от плоскости с началом координат или по разные. Таким образом, искомое расстояние или

,

т.е. расстояние от точки до плоскости равно абсолютной величине результата подстановки координат точки в левую часть нормального уравнения плоскости.

Величина называется отклонением точки от плоскости . При этом , если точки и лежат по разные стороны от плоскости, и , если по одну. Очевидно, .

5. Каноническое уравнение прямой в пространстве.

Пусть заданы точка и ненулевой вектор . Составим уравнение прямой , проходящей через точку параллельно вектору .

Если – произвольная точка прямой то, очевидно, вектор коллинеарен вектору , т.е.

.

Равенство (1.4.29) и есть каноническое уравнение прямой в пространстве.

6. Параметрические уравнения прямой.

Если в (1.4.29) положить, что все соответствующие координаты произвольного вектора прямой и направляющего вектора пропорциональны с коэффициентом пропорциональности , то получим

или

Это и есть параметрические уравнения прямой в пространстве.

7. Прямая в пространстве как линия пересечения двух плоскостей.

Всякие две пересекающиеся плоскости и заданные уравнениями

определяют в пространстве прямую линию , линию их пересечения.

Возникает вопрос: как от общих уравнений прямой и перейти к каноническим уравнениям вида. Для этого нам надо иметь точку и вектор , параллельный . Очевидно, вектор параллельный , будет ортогонален и . Значит, вектор можно найти посредством векторного произведения :

Координаты любой точки , принадлежащей можно найти как решение системы уравнений и , положив, скажем, . Найдя эту точку, по формуле составим искомое уравнение прямой в каноническом виде:

.