РГР / kontrolnaya_rabota_po_oau_4_5_mufazalov_d_f / Задание на рас4-5о

САУ №4

Система управления описывается совокупностью уравнений (4)

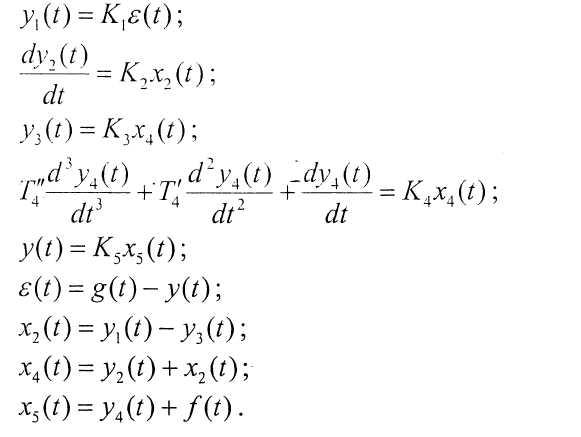
Известные параметры системы управления приведены в таблице ниже. Таблица 4 - Параметры САУ

№	K2	K3	K4			K5
5	8	1.7	3.0	0.076	0.036	5.4

1. Составить структурную схему системы управления по заданной совокупности уравнений.

Составим по дифференциальным уравнениям передаточные функции звеньев

W1(p)=k1

W2(p)=k2/p

W3(p)=k3

W4(p)=k4/(t4’’p³+t4’p²+p)

W5(p)=k5

И структурную схему системы

(рис. 1)

2. Определить передаточные функции замкнутой системы по задающему воздействию, по возмущению, по ошибке.

При оформлении передаточные функции записывать в виде дроби

Составим передаточную функцию замкнутой системы по задающему воздействию:

Ф_g(p)= W_Пр(p)/(1+W_Пр(p))

W_Пр(p)=W1(p)*W23(p)*W4(p)*W5(p)

W23(p)=(W2(p)+1)/(1+(1+W2(p))*W3(p))

W23(p)=(p+k2)/(k3p+k2*k3+1)

W_Пр(p)=k1*(p+k2)*k4*k5/(k3*p+k2*k3+1)/(t4’’p³+t4’p²+p)

k1*k4*k5*(p+k2)

Ф(p)=------------------------------------------------------------------ (1)

(k1*k4*k5(p+k2)+(k3*p+k2*k3+1)(t4’’p³+t4’p²+p))

Составим передаточную функцию замкнутой системы , по возмущению:

Ф_f(p)=W5(p)/(1+ W_Пр(p))

k5*(k3*p+k2*k3+1)*(t4’’p³+t4’p²+p)

Ф_f(p)=------------------------------------------------------------------

( k1*k4*k5(p+k2)+(k3*p+k2*k3+1)(t4’’p³+t4’p²+p))

Составим передаточную функцию замкнутой системы, по ошибке:

Ф_е(p)=1/(1+ W_Пр(p))

(k3*p+k2*k3+1)(t4’’p³+t4’p²+p)

Ф_е(p)=_________________________________________

(k1*k4*k5(p+k2)+ (k3*p+k2*k3+1)(t4’’p³+t4’p²+p))

3. Построить область устойчивости замкнутой системы методом D-разбиения по неизвестному коэффициенту усиления. Выбрать значение этого коэффициента, исходя из условия устойчивости.

Из (1) выразим характеристический полином замкнутой системы

D(p)=(k1*k4*k5(p+k2)+(k3*p+k2*k3+1)(t4’’p³+t4’p²+p))

Из уравнения D(p)=0 выразим неизвестный коэффициент

k1= –(k3*p+k2*k3+1)(t4’’p³+t4’p²+p))/ k5/k4/(p+k2)

перейдем в частотную область p=jω

k1(ω)= ––(k3* jω +k2*k3+1)(t4’’(jω)³+t4’(jω)²+ jω))/ k5/k4/(jω+k2)

k1(w)=0.0617*(-1.7*i*w-14.6)*(-0.0760*i*w^3- 0.036*w^2+i*w)/(i*w+8)

выделим мнимую и действительную части x(w) и y(w) и построим график y(x)

Рис(2)

Выделим на графике область устойчивости и выберем вней значние коэффициента к1.

K1=0,025

2. Оценить устойчивость разомкнутой системы регулирования по критерию Гурвица.

Подставим полученное значение в (1).

Получим

0.405 s + 3.24

Ф(p)=-----------------------------------------------------------------------

0.2052 s^4 + 1.131 s^3 + 3.19 s^2 + 14 s + 3.24

-------------------------------------------------

составим определитель Гурвица И НАЙДЕМ ЕГО значение

1.1308 14.0050 0 0

0.2052 3.1896 3.2400 0

0 1.1308 14.0050 0 = 19.8362>0

0 0.2052 3.1896 3.2400

Найдем значения его главнодиагональных миноров.

1.1308 14.0050 0

0.2052 3.1896 3.2400 = 6.1223>0

0 1.1308 14.0050

1.1308 14.0050

0.2052 3.1896 = 0.7330>0

Определитель Гурвица и все его главнодиагональные миноры положительны, следовательно, по критерию Гурвица система устойчива.

2. Исследовать на устойчивость замкнутую систему управления, используя критерии Михайлова и Найквиста.

Рассмотрим характеристический полином замкнутой системы в частотной области и построим годограф Михайлова

D(s)=0.2052 s^4 + 1.131 s^3 + 3.19 s^2 + 14 s + 3.24

Рис3

Из рисунка видно, что годограф Михайлова проходит через 4 квадранта. порядок системы равен 4, поэтому система по критерию Михайлова устойчива.

Рассмотрим в частотной области передаточную функцию разомкнутой системы

0.405 s + 3.24

Wраз(p)= ------------------------------------------------------------

0.2052 s^4 + 1.131 s^3 + 3.19 s^2 + 13.6 s

и построим годограф Найквиста

рис 4

годограф Найквиста не охватывает точку (-1, 0j), поэтому замкнутая система устойчива.

5.

Построить логарифмические частотные характеристики разомкнутой системы и определить запасы устойчивости по амплитуде и фазе.

Рис 5.

И определим по ней запасы устойчивости: по фазе 88,5 градусов, по амплитуда 6.9 дб.

2. Найти коэффициенты ошибок замкнутой системы.

Передаточная функция замкнутой системы по ошибке имеет вид

0.2052 s^4 + 1.131 s^3 + 3.19 s^2 + 13.6 s Q(p)

Ф_е(p)=----------------------------------------------------------------------------=-----------------------------

0.2052 s^4 + 1.131 s^3 + 3.19 s^2 + 14 s + 3.24 R(p)

Найдем коэффициенты ошибок

С0= Ф_е(0)=0

С1=(Q’(0)R(0)-Q(0)R’(0))/R(0)/R(0)=(3.19*3.24)/3.24/3.24= 0.9846

8. Построить переходную характеристику системы и определить показатели качества управления.

С помощью оператора step построим переходную функцию замкнутой системы

Рис 6.

Показатели качества: время регулирования 16.6 с, перерегулирование отсутствует, установившееся значение 1, перерегулирование 0,0382 %

Листинг программы:

clc

clear

k2=8

k3=1.7

k4=3

k5=5.4

t4=0.076

t5=0.036

%выражение для коэффициента

syms w p

p=1i*w;

k1=-(k3*p+k2*k3+1).*(t4*p.^3+t5*p.^2 +p)/ k5/k4./(p+k2)

%изменение частоты

w=-5:0.015:5;

%построение графика

p=1i*w;

k1=-(k3*p+k2*k3+1).*(t4*p.^3+t5*p.^2 +p)/ k5/k4./(p+k2);

plot(real(k1),imag(k1),'LineWidth',2), grid

%выбираем хначение к1

k1=0.025

%описываем ПФ звеньев

w1=tf(k1)

w2=tf(k2,[1 0])

w3=k3

w4=tf(k4,[t4 t5 1 0])

w5=k5

w23=feedback(w2+1,w3)

%ПФ разомкнутой системы

WR=w1*w23*w4*w5;

%ПФ замкнтуой системы

W=feedback(WR,1)

figure(4)

step(W)

%криетрий гурвица

a=W.den{1}

d4=[a(2) a( 4) 0 0 ; a(1) a(3) a(5) 0 ; 0 a(2) a(4) 0; 0 a(1) a(3) a(5) ]

det(d4)

d3=d4(1:3,1:3)

det(d3)

d2=d3(1:2,1:2)

det(d2)

d1=d2(1:1,1:1)

det(d1)

b=W.den{1};

%критерий Михайлова

w=0:0.01:4;

p=1j*w;

M=polyval(b,p);

figure(2)

plot(real(M),imag(M)),grid

%критерий Найквиста

WR

w=0:0.01:10;

p=1j*w;

M1=polyval(WR.num{1},p)./polyval(WR.den{1},p);

figure(3)

plot(real(M1),imag(M1)),grid

%ЛАХ ЛФХ

figure(5)

margin(WR)

%коэф ошибок

We=1/(1+WR)