34. Понятие о различных видах связей между признаками в совокупности: функциональные и статистические связи. Формы их проявления и возможности статистического анализа и учета.

Классификация связи. По степени тесноты: функциональные (значению факторного признака соответствует только одно значение результативного) и схоластические (случайные).По направлению: прямые, обратные. По аналитическому выражению: линейные (если связь между факторным и результативным признаком можно выразить с помощью уравнения прямой) и нелинейные/криволинейные.

35.Корреляционно-регрессионный метод. Сущность, основные задачи и показатели. Множественная линейная регрессия.

Корреляция оценивает тесноту связи, регрессия исследует ее форму. Задачи корреляционного анализа: 1. Определение тесноты связи. 2. Определение неизвестных причин связи. 3. Определение факторов, влияющих на результативный признак (для каждого фактора строим корреляционное поле, определяем, в каком графике больше теснота связи -г де больше, тот и определяющий). Задачи регрессионного анализа: 1.Выявить форму зависимости. 2. Функцию регрессии составить. 3. Найти неизвестное значение коэффициентов. Сущность: для линейного коэффициента корреляции. 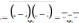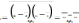В числителе- среднее значение произведения отклонений наблюдаемой переменной от ее среднего значения (ковариация). В знаменателе – среднее квадратическое отклонение. Вообще -1≤r≤1. Для лин.зависимости : 0,7 ≤|r| ≤1 – сильная связь; 0,3 ≤|r|≤0,7 – средняя; 0 ≤|r| ≤0,3 – слабая. R>0 – прямая связь, r<0 – обратная связь. С-ва средней: 1. 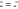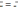; 2. . 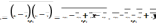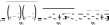следовательно: =0 это если икс итое среднее равно икс среднему. Если игрек не зависит от икс.(обратно нельзя). Регрессия: Рассмотрим пример линейной зависимости. .?-. Их найдем с помощью метода наименьших квадратов (МНК). Нужно, чтобы Е стремилось к минимуму. Функционал: 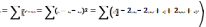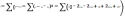. Может быть минимальным, если производная равна 0. Т.к. фун-я двух переменных, то ищем частные производные и решаем систему из двух этих уравнений: 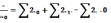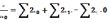& 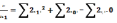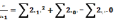. Дальше делим все на 2 и выносим за знак суммы. 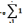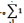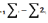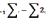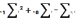Получаем опять систему: +=0 & 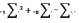=0. Находим а1 и а2. Затем записываем уравнение регрессии. И проводим его.

37. Парная и множественная корреляция. Оценка существенности связи.

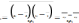
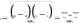
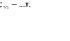
З вида корреляции: парная (связь между двумя признаками:ф и р,или 2 ф), частная – зависимость между результативным и одним факт.признаками при фиксированном значении других ф. множественная(1 р и 2 и более ф.)Оценка существенности связи на основе линейного коэффициента корреляции: . 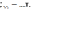В числителе - среднее значение произведения отклонений наблюдаемой переменной от ее среднего значения (ковариация). В знаменателе – среднее квадратическое отклонение. Вообще -1≤r≤1. Для лин.зависимости : 0,7 ≤|r| ≤1 – сильная связь; 0,3 ≤|r|≤0,7 – средняя; 0 ≤|r| ≤0,3 – слабая. R>0 – прямая связь, r<0 – обратная связь. С-ва средней: 1. 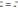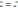; 2. . 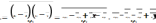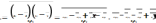следовательно: =0 это если икс итоге среднее равно икс среднему. Если игрек не зависит от икс.(обратно нельзя). Это для парной корреляции, для множественной: С целью расширения возможностей экономического анализа используются частные коэффициенты эластичности: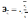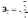,где– среднее значение соответствующего факторного признака; ­­– среднее значение результативного признака; – коэффициент регрессии при соответствующем факторном признаке

Коэффициент эластичности показывает, на сколько % в среднем изменится значение результативного признака при изменении факторного признака на 1 %.Между линейным коэффициентом корреляции и регрессии существует определенная зависимость, выражаемая формулой: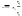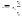,где – коэффициент регрессии в уравнении связи; – среднее квадратическое отклонение соответствующего факторного признака.Проверка адекватности модели проводится по критерию Фишера. 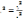Необходимо выполнение условия:,где k=2– число параметров, описывающих теоретическую зависимость, F_теор.(k,n-k)– квантиль распределения Фишера-Снедекора, соответствующая уровню значимости (P{F>F_теор}=альфа).Коэффициент детерминации: 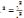,сигма игрек - межгрупповая дисперсия. 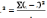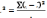общая дисперсия,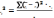 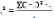. Определяет какая часть факторного признака учтена в общем объеме вариации.