
- •1. Подвижный репер поверхности.
- •1.1.Метод подвижного репера
- •2. Теория кривой.
- •2.2. Регулярная кривая.
- •2.2. Длина дуги. Естественный параметр кривои.
- •2.3. Касательная прямая и нормальная плоскость кривой.
- •2.4. Касательное отображение и касательное расслоение.
- •2.5. Соприкасающаяся плоскость.
- •2.6. Сопровождающий репер кривой.
- •2.7. Кривизна кривой.
- •2.8. Кркучение кривой.
- •2.9. Формулы френе.
- •2.10. Уплощение кривой.
- •2.11. Вычислительные формулы для кривизны и кручения кривой.
- •II.12. Прямая, окружность, винтовая линия.
- •2.13. Задание кривой функциями кривизны и кручения.
- •2.14. Линии постоянных кривизн.
- •2.15. Строение кривой вблизи обыкновенной точки.
- •3. Теория поверхности.
- •3.1. Регулярная поверхность.
- •3.2. Линии на поверхности.
- •3.3. Касательная плоскость и нормаль поверхности.
- •3.4. Первая основная квадратичная форма поверхности.
- •3.5. Метрика на поверхности.
- •3.6. Кривизна линий на поверхности.
- •3.7. Индикатриса кривизны.
- •3.8. Классфикация обыкновенных точек поверхности.
- •3.9. Главные кривизны на поверхности.
- •3.10. Вычисление полной и средней кривизн поверхности.
- •4.Кривая.
- •4.5.Вычислим кручение кривой :
- •4. 6. Изображение кривой.
- •5. Поверхность.
- •5.1. Найдем уравнение касательной плоскости, используя формулу:
- •5.2. Найдем уравнение нормали для искомой поверхности.
- •5.4.Вычисление второй квадратичной формы.
- •5.5.Вычисление полной кривизны поверхности
- •5.6. Вычисление средней кривизны поверхности.
- •5.7. Изображение поверхности.
3.4. Первая основная квадратичная форма поверхности.
В
произвольной точке
 поверхности
поверхности
 зададим направление, выбрав
зададим направление, выбрав
 ,
,
 .
Отношение дифференциалов
.
Отношение дифференциалов

определяет направление на поверхности, имеем
 .
.
Производная
от
 по направлению
по направлению
 имеет вид
имеет вид
 .
.
Малое
смещение
 по кривой
по кривой
 на поверхности вычисляется на основании
равенств
на поверхности вычисляется на основании
равенств
 .
.
Отсюда
получаем, вычисляя скалярный квадрат
 ,
,
 .
(3.4.1)
Введем
обозначения:
.
(3.4.1)
Введем
обозначения:
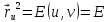 ,
,  ,
,  .
(3.4.2)
Значения этих скалярных произведений
зависят от выбора точки
.
(3.4.2)
Значения этих скалярных произведений
зависят от выбора точки
 поверхности. Выражение
поверхности. Выражение
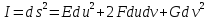 .
(3.4.3)
называется
первой
основной квадратичной формой поверхности
.
(3.4.3)
называется
первой
основной квадратичной формой поверхности
 .
.
3.5. Метрика на поверхности.
Малое
расстояние
 на поверхности
на поверхности
 в
направлении
в
направлении
 может быть найдено по первой квадратичной
форме
может быть найдено по первой квадратичной
форме
 .
.
На этом основании первая квадратичная форма поверхности определяет метрику на поверхности. Матрица Грама этой метрики:
 ,
,
 ,
,
Детерминант метрической формы равен
 .
.
Для
любых векторов
 и
и
 , угол между которыми равен
, угол между которыми равен
 ,
имеем
,
имеем
 ,
,
 ,
,
поэтому верно соотношение
 .
.
Перепишем
это равенство для
 ,
,
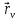 :
:
 .
.
Отсюда, используя обозначения (III.4.2), находим:
 ,
,
 .
(3.5.1)
.
(3.5.1)
Вместе с тем, получено

и детерминант первой квадратичной формы есть ее дискриминант.
Длину
дуги кривой, проходящей через точку
 в направлении
в направлении
 можно вычислить на основании дифференциала
дуги
можно вычислить на основании дифференциала
дуги
 (3.4.1):
(3.4.1):

 .
.
Если
через точку
 проходит еще одна линия
проходит еще одна линия
 в направлении
в направлении
 ,
то угол
,
то угол
 между кривыми
между кривыми
 и
и
 есть угол между векторами
есть угол между векторами
 и
и
 и может быть найден из формулы
и может быть найден из формулы
 .
.
Если
первое направление есть направление
-линии:
 ,
,
 ,
второе направление есть направление
,
второе направление есть направление
 -линии:
-линии:
 ,
,
 ,
и
,
и
 угол между
угол между
 -линией
и
-линией
и
 -линией,
то
-линией,
то
 .
.
Выполняется
 .
.
Элемент площади фигуры на поверхности равен

и по (3.5.1):
 .
.
Теперь
площадь фигуры
 ,
лежащей на поверхности
,
лежащей на поверхности
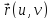 ,
вычисляется по формуле
,
вычисляется по формуле
 .
.
Итак,
на основании первой квадратичной формы
 (3.4.3) поверхности
(3.4.3) поверхности
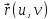 на поверхности вычисляются длины линий
между заданными точками, углы между
линиями и площади фигур, лежащих на
поверхности, т.е. могут быть произведены
все измерения. Форма
на поверхности вычисляются длины линий
между заданными точками, углы между
линиями и площади фигур, лежащих на
поверхности, т.е. могут быть произведены
все измерения. Форма
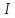 действительно является метрической.
действительно является метрической.
3.6. Кривизна линий на поверхности.
На
поверхности рассматриваем линию
рассматриваем линию
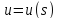 ,
,
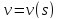 в естественной параметризации
в естественной параметризации
 .
.
Согласно
п. II.7,
кривизна кривой
 определяется из равенства
определяется из равенства
 ,
,
где
 кривизна кривой,
кривизна кривой,
 единичный вектор главной нормали кривой.
Обозначим
единичный вектор главной нормали кривой.
Обозначим
 единичный вектор нормали поверхности
единичный вектор нормали поверхности
 ,
это вектор
,
это вектор
 (3.6.1)
см.
п. 3.3. Умножим скалярно
(3.6.1)
см.
п. 3.3. Умножим скалярно
 и
и
 :
:
 ,
,
если
 угол между
угол между
 и
и
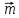 .
Величина
.
Величина

называется
нормальной кривизной кривой
 на поверхности
на поверхности
 или нормальной кривизной поверхности:
или нормальной кривизной поверхности:
 (3.6.2)
Вычислим
(3.6.2)
Вычислим
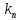 в окрестности точки
в окрестности точки
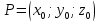 .
Находим
.
Находим
 ,
,
 ,
,
 ,
,
Здесь
 и
и
 ,
так как
,
так как
 .
Обозначим
.
Обозначим
 ,
,
 ,
,
 .
.
На основании (3.6.1) и (3.6.2) имеем
 ;
;
 ;
;
 .
.
Коэффициенты
 ,
,
 ,
,
 вычислены в точке
вычислены в точке
 поверхности. Выражение для нормальной
кривизны линии на поверхности таково:
поверхности. Выражение для нормальной
кривизны линии на поверхности таково:
 .
(3.1.3)
.
(3.1.3)
Отсюда получаем
 .
.
Воспользуемся
значением
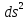 из первой квадратичной формы (3.4.3)
поверхности
из первой квадратичной формы (3.4.3)
поверхности
 (3.6.4)
(3.6.4)
Квадратичная форма

называется второй квадратичной формой поверхности. Таким образом, нормальная кривизна поверхности есть отношение второй и первой квадратичных форм поверхности.
Рассмотрим
на поверхности кривые, проходящие через
точку
 и имеющие с кривой
и имеющие с кривой
 общую соприкасающуюся плоскость. У этих
кривых общий вектор касательной
общую соприкасающуюся плоскость. У этих
кривых общий вектор касательной
 и общий вектор кривизны
и общий вектор кривизны
 .
Среди этих кривых находится плоская
кривая, лежащая в соприкасающейся
плоскости
.
Среди этих кривых находится плоская
кривая, лежащая в соприкасающейся
плоскости
 ,
эта плоскость содержит и нормаль
,
эта плоскость содержит и нормаль
 поверхности. Следовательно, выполняется
поверхности. Следовательно, выполняется
3.1.1.
ТЕОРЕМА.
Нормальная
кривизна поверхности в точке
 есть
кривизна нормального сечения поверхности.
#
есть
кривизна нормального сечения поверхности.
#
