
- •1. Подвижный репер поверхности.
- •1.1.Метод подвижного репера
- •2. Теория кривой.
- •2.2. Регулярная кривая.
- •2.2. Длина дуги. Естественный параметр кривои.
- •2.3. Касательная прямая и нормальная плоскость кривой.
- •2.4. Касательное отображение и касательное расслоение.
- •2.5. Соприкасающаяся плоскость.
- •2.6. Сопровождающий репер кривой.
- •2.7. Кривизна кривой.
- •2.8. Кркучение кривой.
- •2.9. Формулы френе.
- •2.10. Уплощение кривой.
- •2.11. Вычислительные формулы для кривизны и кручения кривой.
- •II.12. Прямая, окружность, винтовая линия.
- •2.13. Задание кривой функциями кривизны и кручения.
- •2.14. Линии постоянных кривизн.
- •2.15. Строение кривой вблизи обыкновенной точки.
- •3. Теория поверхности.
- •3.1. Регулярная поверхность.
- •3.2. Линии на поверхности.
- •3.3. Касательная плоскость и нормаль поверхности.
- •3.4. Первая основная квадратичная форма поверхности.
- •3.5. Метрика на поверхности.
- •3.6. Кривизна линий на поверхности.
- •3.7. Индикатриса кривизны.
- •3.8. Классфикация обыкновенных точек поверхности.
- •3.9. Главные кривизны на поверхности.
- •3.10. Вычисление полной и средней кривизн поверхности.
- •4.Кривая.
- •4.5.Вычислим кручение кривой :
- •4. 6. Изображение кривой.
- •5. Поверхность.
- •5.1. Найдем уравнение касательной плоскости, используя формулу:
- •5.2. Найдем уравнение нормали для искомой поверхности.
- •5.4.Вычисление второй квадратичной формы.
- •5.5.Вычисление полной кривизны поверхности
- •5.6. Вычисление средней кривизны поверхности.
- •5.7. Изображение поверхности.
2.4. Касательное отображение и касательное расслоение.
При
движении точки
 по кривой
по кривой
 вектор
вектор
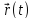 изменяется. Имеем отображение точек
кривой в векторное пространство при
каждом значении
изменяется. Имеем отображение точек
кривой в векторное пространство при
каждом значении
 :
:
 .
.
Это
касательное
отображение вдоль кривой
 .
Рассмотрев всевозможные кривые евклидова
пространства
.
Рассмотрев всевозможные кривые евклидова
пространства
 ,
проходящие через точку
,
проходящие через точку
 ,
и касательные отображения вдоль этих
кривых, имеем
касательное отображение евклидова
пространства
,
и касательные отображения вдоль этих
кривых, имеем
касательное отображение евклидова
пространства
 в
его векторное пространство
в
его векторное пространство
 в
точке
в
точке
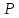 .
Множество касательных отображений
.
Множество касательных отображений
 во всех точках
во всех точках
 называется касательным
расслоением.
называется касательным
расслоением.
2.5. Соприкасающаяся плоскость.
Рассмотрим
плоскости, проходящие через касательную
кривой
 в точке
в точке
 кривой. При изменении параметра
кривой. При изменении параметра
 получаем вектор
получаем вектор
 .
Для вектора
.
Для вектора
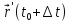 имеет место формула Тейлора
имеет место формула Тейлора
 ,
,
 бесконечно
малое векторное слагаемое, более высокого
порядка, чем
бесконечно
малое векторное слагаемое, более высокого
порядка, чем
 .
Точка
.
Точка
 кривой и касательная
кривой и касательная
 определяют плоскость
определяют плоскость
 .
Нормальный вектор этой плоскости есть
.
Нормальный вектор этой плоскости есть
 .
Найдем нормаль плоскости
.
Найдем нормаль плоскости
 при
при
 ,
т.е. при
,
т.е. при
 .
Имеем
.
Имеем


При
 второе слагаемое стремится к
второе слагаемое стремится к
 быстрее, чем
быстрее, чем
 .
Следовательно, нормали рассматриваемых
плоскостей незначительно отличаются
от вектора
.
Следовательно, нормали рассматриваемых
плоскостей незначительно отличаются
от вектора
 . (мы рассматриваем регулярные кривые,
этот вектор существует.) С уменьшением
. (мы рассматриваем регулярные кривые,
этот вектор существует.) С уменьшением
 уменьшается длина вектора нормали,
направление ее стремится к неизменному
направлению
уменьшается длина вектора нормали,
направление ее стремится к неизменному
направлению
 .
.
Плоскость
 называется соприкасающейся
плоскостью кривой в точке
называется соприкасающейся
плоскостью кривой в точке
 .
Уравнение соприкасающейся плоскости
.
Уравнение соприкасающейся плоскости
 .
.
2.5.1. ТЕОРЕМА. Положение соприкасающейся плоскости не зависит от параметризации кривой.
#
Рассматриваем кривую в произвольной
параметризации
 и в естественной параметризации
и в естественной параметризации
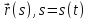 .
Имеем
.
Имеем
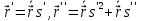 .
Линейные пространства
.
Линейные пространства
 и
и
 совпадают, следовательно, совпадают и
плоскости
совпадают, следовательно, совпадают и
плоскости
 ,
,
 .
#
.
#
Касательная прямая и соприкасающаяся плоскость называются еще соответственно первой и второй соприкасающимися плоскостями кривой. Соединяем теоремы 2.3.1 и 2.5.1:
2.5.2. ТЕОРЕМА. Соприкасающиеся плоскости регулярной кривой существуют, их положение не зависит от параметризации кривой. #
2.6. Сопровождающий репер кривой.
Пусть
 ,
регулярная
класса
,
регулярная
класса
 кривая. Во всякой ее обыкновенной точке
кривая. Во всякой ее обыкновенной точке
 существует касательная
существует касательная
 единичный вектор касательной, см. пп.
II.2 и II.3. Имеем
единичный вектор касательной, см. пп.
II.2 и II.3. Имеем
 и по лемме 2.2.3,
и по лемме 2.2.3,
 , т.е.
, т.е.
 . Вектор
. Вектор
 определяет нормаль
определяет нормаль
 кривой
кривой
 в точке
в точке
 ,
она называется главной
нормалью
кривой
,
она называется главной
нормалью
кривой
 в точке
в точке
 .
Кривая в любой своей точке имеет
бесконечно много нормалей, составляющих
нормальную плоскость кривой. Вектор
.
Кривая в любой своей точке имеет
бесконечно много нормалей, составляющих
нормальную плоскость кривой. Вектор
 называется единичным
вектором главной нормали кривой.
Вектором бинормали
называется вектор, перпендикулярный
соприкасающейся плоскости кривой,
единичный
вектор бинормали
обозначается
называется единичным
вектором главной нормали кривой.
Вектором бинормали
называется вектор, перпендикулярный
соприкасающейся плоскости кривой,
единичный
вектор бинормали
обозначается
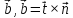 ,
имеем
,
имеем
 ,
точнее,
,
точнее,
 ,
,
 есть
векторное произведение векторов
есть
векторное произведение векторов
 .
Прямая
.
Прямая
 называется бинормалью
кривой.
называется бинормалью
кривой.
С
кривой связан сопровождающий
репер
 ,
,
 точка движется по кривой. Координатные
оси:
точка движется по кривой. Координатные
оси:
 - касательная, <
- касательная, < главная нормаль,
главная нормаль,
 -
бинормаль. Координатные плоскости:
-
бинормаль. Координатные плоскости:
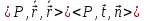 - соприкасающаяся,
- соприкасающаяся,
 -
нормальная,
-
нормальная,
 - спрямляющая.
- спрямляющая.
2.7. Кривизна кривой.
На
регулярной кривой
 возьмем точку
возьмем точку
 и точку
и точку
 .
Угол между касательными
.
Угол между касательными
 и
и
 обозначим через
обозначим через
 .
Изменению
.
Изменению
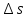 параметра
параметра
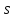 соответствует изменение
соответствует изменение
 угла между касательными. Обозначим:
угла между касательными. Обозначим:
 .
.
Имеем:
 ,
это скорость вращения единичного вектора
касательной;
,
это скорость вращения единичного вектора
касательной;
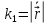 .
Таким образом, справедливо равенство
.
Таким образом, справедливо равенство
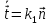 и
и
 .
.
Во
всякой точке кривой
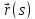 :
:
 и
и
 .
.
Величина
 называется кривизной
или первой
кривизной
кривой
называется кривизной
или первой
кривизной
кривой
 в точке
в точке
 функция
функция
 называется функцией
кривизны
кривой
называется функцией
кривизны
кривой
 ,
,
 ,
,
 - вектор
кривизны
кривой
- вектор
кривизны
кривой
 .
Величина
.
Величина
 называется радиусом
кривизны
кривой
называется радиусом
кривизны
кривой
 в точке
в точке
 .
В направлении вектора кривизны
.
В направлении вектора кривизны
 откладывается отрезок
откладывается отрезок
 .
Окружность
.
Окружность
 с центром
с центром
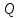 и радиусом
и радиусом
 называется окружностью кривизны в точке
называется окружностью кривизны в точке
 или соприкасающейся окружностью кривой
или соприкасающейся окружностью кривой
 в токе
в токе
 .
Она касается кривой
.
Она касается кривой
 и ее касательной в точке
и ее касательной в точке
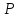 .
.
