Сведем данные для расчета в таблицу

Обозначение размера	Размер	xj	Ecj	Tj	aj	aj	Ecj+aj	xj (Ecj+aj)
А1	27(-0,12)	+1	-0,06	0,12	+0,2	0,012	-0,048	-0,048
А2	142	+1	Ec2	0,69	+0,2	0,069	Ec2+0,069	+(Ec2+0,069)
А3	27(-0,12)	+1	-0,06	0,12	+0,2	0,012	-0,048	-0,048
А4		-1	0	0,46	0	0	0	0

По уравнению (10)

найдем среднее отклонение размера А₂.

0 = -0,048 + (Е_с2 + 0,069) -0,048

Е_с2 = +0,027 мм.

Предельные отклонения размера А₂:

ES₂ = +0,027 + 0,5×0,69= +0,372 мм;

EI₂ = +0,027 - 0,5×0,69= -0,318 мм.

Т.о.

А₂ = мм.

Обратная задача

Найти предельные значения замыкающего размера при значениях составляющих размеров, полученных в результате решения примера 3.

Расчет произвести вероятностным методом, исходя из допустимого процента брака на сборке, равного 0,27%.

Сведем данные для расчета в таблицу

Обоз. размеров	Размер
А1	27(-0,12)	+1	-0,06	0,12	+0,2	0,012	-0,048	-0,048	0,12	0,0144
А2		+1	+0,027	0,69	+0,2	0,069	0,096	+0,096	0,69	0,4761
А3	27(-0,12)	+1	-0,06	0,12	+0,2	0,012	-0,048	-0,048	0,12	0,0144
А4		-1	0	0,46	0	0	0	0	0,46	0,2116

1. Номинальное значение замыкающего размера:

= 27 + 142 + 27 –195 = 1 мм.

2. Среднее отклонение замыкающего размера:

мм.

3. Допуск замыкающего размера:

мм.

4. Предельные значения замыкающего размера:

мм;

мм.

5. Сравним полученные результаты с заданными

.

Следовательно, изменения предельных отклонений составляющих размеров не требуется.

Часть3

Обработка результатов многократных измерений

В табл.1 приведены 100 независимых числовых значений результата измерения X, каждое из которых повторилось m раз. Доверительная вероятность P=0,9.

табл. 1

X	m	X	m	X	m
14.97 15.04 15.15 15.17 15.18 15.19 15.2 15.21 15.22 15.23 15.24 15.25 15.26	1 1 1 2 1 3 1 2 1 5 4 4 2	15.27 15.28 15.29 15.3 15.31 15.32 15.33 15.34 15.35 15.36 15.37 15.38 15.39	5 6 5 4 4 2 3 10 4 1 3 2 3	15.4 15.41 15.42 15.43 15.44 15.45 15.46 15.49 15.52 15.54 15.56	3 1 3 3 1 1 2 3 1 1 1

1.Определяем среднее арифметическое и стандартное отклонение для данных табл.1: ; .

2. С помощью правила « трех сигм» проверяем наличие или отсутствие промахов.

Таким образом, ни один из результатов не выходит за границы интервала, следовательно, с вероятностью 0,9973 гипотеза об отсутствии грубых погрешностей принимается.

3. Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.

Для этого, чтобы построить гистограмму, необходимо результаты отдельных измерений расположить в так называемый вариационный ряд по возрастанию их численных значений( в рассматриваемом примере эта процедура уже проделана и представлена табл.1)

Участок оси абсцисс, на котором располагает вариационный ряд значений физической величины, разбивается на k одинаковых интервалов. Выбор числа интервалов k=10 :

.

Выбор начала первого интервала в точке 14,941, тогда конец последнего(11-го) интервала окажется в точке 15,590

Затем для каждого интервала подсчитывается количество результатов , попавших в данный интервал и определяется

(Результаты приведены в табл.2)

Общее число интервалов становится равным 7.

4. Проверка нормальности закона распределения по критерию Пирсона.

Если выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используется функция Лапласа:

, и определяем по таблице.

Найдя таким образом значения Р_i для каждого интервала k_i , заполним соответствующие ячейки таблицы 2, а затем рассчитаем значение _-- критерия для каждого интервала и, наконец суммарное значение :

Определим табличное значение 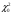, задавшись доверительной вероятностью 0,9 и вычислив по формуле r=k-3 число степеней свободы:

r =k-3=10-3 =7 ;

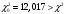
Таким образом, с вероятностью 0,9 гипотеза о нормальности распределения вероятности результата измерения принимается.

5. В тех же координатах , что и гистограмма , следует построить теоретическую кривую плотности вероятности . Для этого рассчитываются значения плотности вероятности для середина каждого интервала p_i=P_i/ и откладываются как ординаты из середины соответствующих интервалов , полученные точки соединяют плавной кривой , симметричной относительно математического ожидания .

6. Представление результатов в виде доверительного интервала.

Для этого определим стандартное отклонение среднего арифметического по формуле:

Закон распределения вероятности для среднего арифме­тического считаем нормальным (что следует из нормальности распределения самой изме­ряемой величины), тогда доверительный интервал определяется по выражению () при до­верительной вероятности 0,9. Этому значению соответствует аргумент функции Лапласа t = 1,65.

В случае, если закон распределения вероятности для среднего арифметического счи­тается неизвестным, то относительный доверительный интервал рассчитывается в соответст­вии с неравенством Чебышева :

; t=3.16

Как видно из сравнения результатов, неизвестность закона распределения вероятно­сти приводит к расширению доверительного интервала, то есть к увеличению дефицита из­мерительной информации.

табл.2

i	Xi-1	Xi	m		ti-1	ti	Фi-1	Фi	Pi
1	14.941	15	1
2	15	15.059	1	0.211864	-3.21186	-1.21186	-0.4993	-0.3869	0.1124	3.264199
3	15.059	15.118	0
4	15.118	15.177	3
5	15.177	15.236	13	2.20339	-1.21186	-0.71186	-0.3869	-0.2611	0.1258	0.014022
6	15.236	15.295	26	4.40678	-0.71186	-0.21186	-0.2611	-0.0832	0.1779	3.288876
7	15.295	15.354	27	4.576271	-0.21186	0.288136	-0.0832	0.1141	0.1973	2.378809
8	15.354	15.413	13	2.20339	0.288136	0.788136	0.1141	0.2852	0.1711	0.987265
9	15.413	15.472	10	1.694915	0.788136	1.288136	0.2852	0.4015	0.1163	0.228452
10	15.472	15.531	4	0.508475	1.288136	2.288136	0.4015	0.4887	0.0872	0.84844
11	15.531	15.59	2