Тема 4. Канонічне розкладання випадкових процесів

Елементарним випадковим процесом називається процес, який має вигляд , де V – звичайна центрована випадкова величина з характеристиками m_V=0, D_V ; – звичайна (невипадкова) функція часу. Для математичного сподівання та кореляційної функції елементарного випадкового процесу маємо:

; (2.7)

Канонічним розкладанням випадкового процесу X(t) називається вираз вигляду

. (2.8)

У цьому виразі являє собою математичне сподівання випадкового процесу X(t); V₁,…,V_i,… – некорельовані, центровані випадкові величини із дисперсіями D₁,…,D_i,…; – невипадкові функції аргументу t. Випадкові величини V₁,…,V_i,… називаються коефіцієнтами канонічного розкладання, а невипадкові функції – координатними функціями канонічного розкладання. Канонічне розкладання може вміщати як скінченне так і нескінченне число членів розкладання.

Характеристики випадкового процесу X(t), заданого своїм канонічним розкладанням, мають вигляд:

; (2.9)

, (2.10)

оскільки ;

. (2.11)

Вираз (2.10) називається канонічним розкладанням кореляційної функції випадкового процесу X(t), а вираз (2.11) – канонічним розкладанням дисперсії.

Тема 5. Стаціонарні випадкові процеси

Стаціонарним називається випадковий процес , математичне сподівання якого є сталою величиною при всіх значеннях аргументу , а кореляційна функція залежить лише від різниці аргументів , тобто

, . (3.1)

Дисперсія . (3.2)

Властивості кореляційної функції.

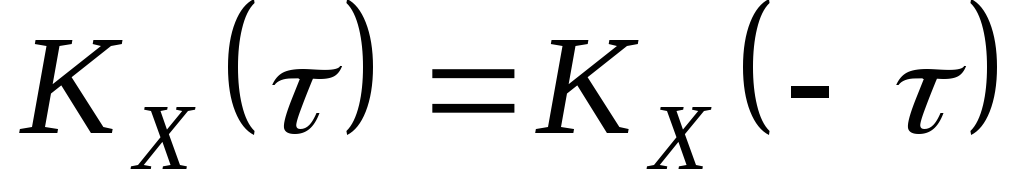1. . 2. .

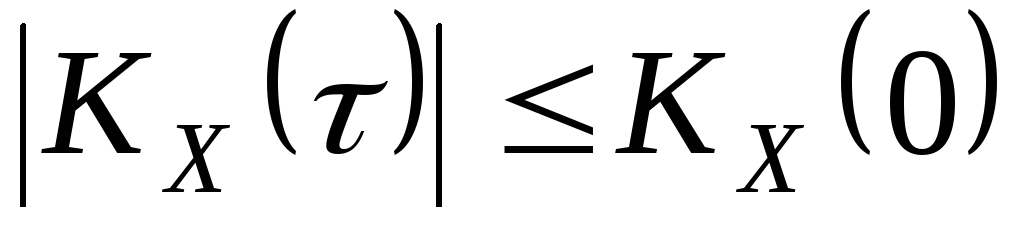Нормованою кореляційною функцією стаціонарного випадкового процесу називається невипадкова функція аргументу :

. (3.3)

Абсолютна величина .

Стаціонарно зв'язаними називаються два випадкових процеси і , взаємна кореляційна функція яких залежить від різниці аргументів .

Не всякі дві стаціонарні функції стаціонарно зв'язані; з іншого боку, дві нестаціонарні функції можуть бути стаціонарно зв'язаними.

Для того, щоб стаціонарний випадковий процес був диференційованим, достатньо існування другої частинної похідної від кореляційної функції при нульовому значенні її аргументу:

. (3.4)

Похідна стаціонарного процесу є стаціонарним процесом. Отже, властивість стаціонарності мають стаціонарні лінійні комбінації стаціонарних процесів та їх похідних (при стаціонарній зв’язаності процесів будь-які їх похідні теж зв’язані стаціонарно).

Кореляційна функція похідної диференційованого стаціонарного випадкового процесу знаходиться за формулою:

. (3.5)

Кореляційну функцію та дисперсію інтегралу від стаціонарного випадкового процесу знаходять відповідно за формулами:

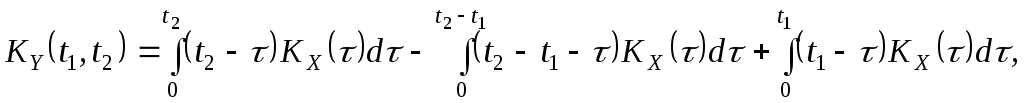
(3.6)

. (3.7)

Заняття 7. Спектральна щільність стаціонарного випадкового процесу.

Спектральною щільністю стаціонарного випадкового процесу називається функція , яка зв'язана з кореляційною функцією взаємно оберненим перетворенням Фур'є:

(3.8)

Ці формули називають формулами Вінера-Хінчина. В дійсній формі вони мають вигляд:

(3.9)

Нормованою спектральною щільністю стаціонарного випадкового процесу називається функція

. (3.10)

Для нормованої кореляційної функції і нормованої спектральної щільності , взаємної кореляційної функції і взаємної спектральної щільності також справедливі формули Вінера-Хінчина.