Состав атмосферы Способы выражения состава чистого и загрязненного воздуха Основные понятия и расчетные формулы

С позиций химии воздух можно рассматривать как газовый раствор – смесь равномерно распределенных друг в друге веществ. Поэтому при описании такой системы удобно использовать термины характерные для растворов. Любой компонент воздуха и загрязнитель (если последний представляет собой газ) будем называть растворенным веществом; чистый воздух, а также смесь воздуха и загрязнителей – раствором. В первом случае он состоит из азота, кислорода, инертных газов и необходимого количества других веществ. Во втором к этим компонентам добавляется один или несколько загрязнителей.

Предположим, что раствор состоит из нескольких компонентов: 1, 2, 3, ..., i, ..., n. Любая величина с индексом i относится к i-му растворенному веществу. Для выражения состава чистого и загрязненного воздуха чаще всего используются приведенные далее величины.

1. Количество частиц в 1 см³ раствора n_i показывает, сколько частиц i -го растворенного вещества содержится в 1 см³ раствора.

Такими частицами для атмосферного воздуха могут быть молекулы, атомы, ионы, радикалы и электроны. Единица измерения количества частиц в 1 см³ раствора – 1/см³.

2. Массовая концентрация равна массе растворенного вещества , отнесенной к объему раствора :

. (1.1)

Единица измерения массовой концентрации – кг/м³.

3. Массовая доля – отношение массы i-го растворенного вещества к массе раствора

. (1.2)

Массовая доля – величина безразмерная. Она может быть выражена в долях единицы (формула (1.2)) или в массовых процентах (сокращенно % (масс.), формула (1.3))

. (1.3)

4. Объемная доля – это отношение объема i -го растворенного вещества к объему раствора

. (1.4)

Объемная доля является безразмерной величиной и выражается в долях единицы (формула (1.4)) или в объемных процентах (сокращенно % (об.), формула (1.5))

. (1.5)

5. Безразмерная величина (от английского parts per million – частей на миллион). Таким образом, показывает, сколько объемных частей i-го растворенного вещества приходится на миллион таких же по объему частей раствора.

Если задаться объемом раствора 1 м³, то для объем растворенного вещества будет равен 1 см³

. (1.6)

Следует отметить, что в данном пособии рассмотрены лишь объемные . Это связано с тем, что массовые используются в литературе значительно реже.

Обозначение 5 ppm показывает, что в миллионе объемных частей воздуха содержится 5 таких же по объему частей газообразной примеси. Для выражения состава раствора с помощью используется также и другое обозначение – млн ^-1. Запись 5 млн ^-1 аналогична 5 ppm.

6. Безразмерная величина . Используется для очень малых концентраций газообразных примесей в воздухе вместо . Название происходит от американского parts per billion – частей на миллиард ( в Америке называется биллионом, а в Европе – миллиардом).

Следовательно, показывает, сколько объемных частей i -го растворенного вещества приходится на миллиард таких же по объему частей раствора.

При 1 в 1 м³ раствора содержится 1 мм³ растворенного вещества

. (1.7)

Обозначение 1 млрд ^-1 тождественно 1 ppb.

Пересчет состава раствора из одних единиц измерения в другие показан ниже.

1. Массовые концентрации и массовые доли.

Обозначим массовые концентрации компонентов раствора как ; единица измерения – кг/м³. Их сумма равна массе одного кубического метра раствора, а это не что иное, как плотность раствора , кг/м³. Таким образом, массовая доля любого компонента может быть рассчитана через его массовую концентрацию , которая представляет собой массу растворенного вещества, содержащуюся в одном кубическом метре раствора, по следующей формуле:

, (1.8)

и наоборот

. (1.9)

Поскольку количество загрязнителей в воздухе обычно много меньше количества самого воздуха, то в этих случаях можно плотность раствора принять равной плотности воздуха. В приближении идеального газа плотность воздуха при нормальных условиях (температура ; давление ) равна отношению его молярной массы к молярному объему

, (1.10)

где (для сухого воздуха), . При условиях, отличных от нормальных (другая температура Т и давление р), плотность воздуха вычисляется по формуле

. (1.11)

2. Количества частиц в 1 см³ раствора и массовые концентрации.

Как уже было сказано ранее, массовая концентрация i-го растворенного вещества в кг/м³ – это его масса в кг, содержащаяся в 1 м³ раствора. Тогда количество i -го растворенного вещества в 1 см³ раствора – , где – молярная масса i -го растворенного вещества, кг/моль . Следовательно, количество частиц i -го растворенного вещества в 1 см³ раствора связано с его массовой концентрацией следующим образом

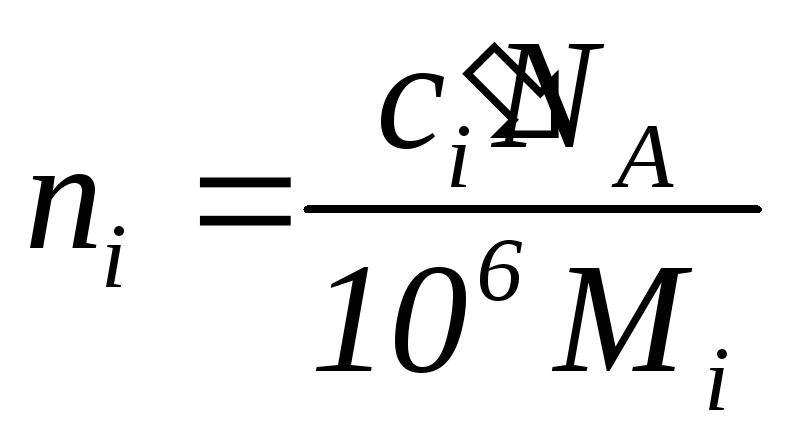, (1.12)

где – постоянная Авогадро.

3. Массовые доли и объемные доли.

Преобразуем формулу (1.2), заменив массы произведениями соответствующих плотностей и объемов

, (1.13)

где – плотность растворенного вещества. Используя формулу (1.4), получим

(1.14)

или

. (1.15)

Если сделать допущение о том, что воздух и газовые примеси являются идеальными газами и использовать соотношение (1.11) вместе с аналогичным выражением для i -го компонента

, (1.16)

то можно получить

(1.17)

или

. (1.18)

4. Объемные доли, и .

Исходя из определений объемной доли, и , нетрудно записать связывающие их соотношения

, (1.19)

, (1.20)

, (1.21)

, (1.22)

. (1.23)

5. Массовые концентрации и объемные доли.

Приравняв правые части уравнений (1.8) и (1.14), после сокращения получим

. (1.24)

6. Массовые концентрации, и .

Выразив из уравнений (1.19) и (1.22) и подставив их поочередно в уравнение (1.24), получим

, (1.25)

. (1.26)

Для идеального газа можно воспользоваться соотношением (1.16), подставив его в уравнения (1.25) и (1.26). Конечные формулы принимают вид

, (1.27)

. (1.28)

7. Количества частиц в см³, и .

Подставляя поочередно уравнения (1.27) и (1.28) в уравнение (1.12) и проводя сокращения, получим

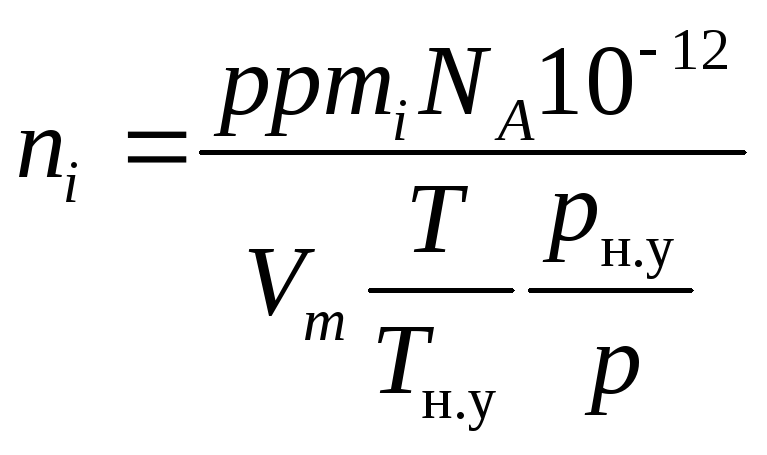, (1.29)

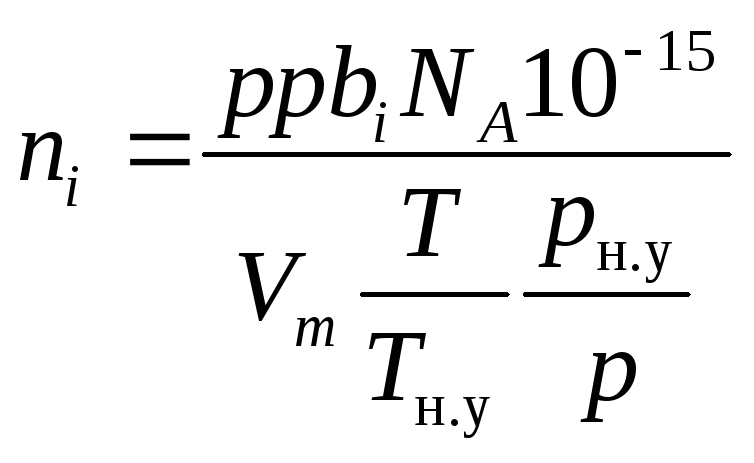. (1.30)

Такая форма представления позволяет учесть поправки на температуру и давление, которые приводят молярный объем идеального газа к условиям, отличным от нормальных.

Обозначив стрелками ( ) выведенную связь, допускающую взаимный перевод, между двумя способами выражения состава чистого и загрязненного воздуха, приведем следующую схему

Безусловно, можно было бы остановиться еще на ряде формул, непосредственно связывающих между собой вышеуказанные величины. Однако не будем этого делать из методических соображений, так как в разделе уже даны соотношения, позволяющие при любом способе выражения состава рассчитать массовую концентрацию , а затем вычислить другую интересующую величину (см. схему).