3.5. Построение проектируемой зубчатой передачи.

По вычисленным на ЭВМ параметрам проектируемая зубчатая передача строится следующим образом.

1. Откладывается межосевое расстояние и проводятся окружности: начальные , ; делительные , ; основные , ; окружности вершин , и впадин , . Начальные окружности должны соприкасаться в полюсе зацепления. Расстояние между делительными окружностями по осевой линии равно воспринимаемому смещению ym. Расстояние между окружностями вершин одного колеса и впадин другого, измеренное по осевой линии, должно быть равно радиальному зазору .

2. Через полюс зацепления касательно к основным окружностям колес проводится линия зацепления. Точки касания и называются предельными точками линии зацепления. Линия зацепления образует с перпендикуляром, восстановленным к осевой линии в полюсе, угол зацепления . Буквами и отмечена активная линия зацепления. Точка является точкой пересечения окружности вершин колеса с линией зацепления, ее называют точкой начала зацепления; точка - точка пересечения окружности вершин шестерни с линией зацепления, ее называют точкой конца зацепления.

3. На каждом колесе строятся профили трех зубьев, причем точка контакта К должна располагаться на активной линии зацепления. Профили зубьев шестерни перенесены на чертеж проектируемой передачи со схемы станочного зацепления с помощью шаблона; эвольвентная часть профиля зуба колеса строится обычным образом, как траектория точки прямой при перекатывании ее по основной окружности без скольжения, и переносится в точку контакта зубьев К на линию зацепления. От построенного профиля зуба откладывается толщина зуба по делительной окружности и проводится аналогичный профиль другой стороны зуба. Профили двух других зубьев располагаются на расстоянии шага . На зубьях, соприкасающихся в точке К, отмечаются активные профили, которые взаимодействуют в процессе зацепления. Нижние точки активных профилей лежат на пересечении окружностей и соответствующих профилей. Активные профили перекатываются друг по другу со скольжением, поэтому их длины различны.

Z1	Z2	m,мм	X1	X2	aw,град	y
15	18	5	0.6	0.5	27.193	4.658
aw,мм	ea	l1	l2	J	sa1/m
87.158	0.992	1.434	1.380	0.506	0.567

3.6. Проектирование планетарного зубчатого механизма.

Дано:

Число сателлитов в редукторе к=3,

Схема редуктора: с двумя внешними зацеплениями.

Передаточное отношение редуктора:

Примем

Уравнение передаточного отношения:

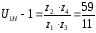
Из условия соосности z₁+z₂=z₃+z₄, получим:

;

Рассмотрим вариант:

Общий множитель q подбирается так, чтобы все числа зубьев были целыми и ;;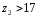 ; . Наименьшим целым q является q=1:

Теперь проверяем, как выполняются условия сборки, соседства и соосности.

Уравнение соосности ( при равных модулях во всех зацеплениях механизма):

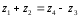; 48 + 48 = 118-22; 96= 96

Уравнение сборки:

;

Данное соотношение выполняется при P=40.

Уравнение соседства:

; ;

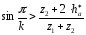0,866 > 0,52

Все три условия выполняются.

На листе вычерчиваем схему редуктора в двух проекциях в масштабе .

u1h	k	Z1	Z2	Z3	Z4
	3	48	48	22	118