1.3.4. Построение графика суммарного приведенного момента.

Строим, складывая с учетом знака ординаты графиков и.

1.3.5. Построение переменных приведенных моментов инерции звеньев II группы

_{Звенья механизма делят на две группы. В первую группу входит начальное звено и все звенья, связанные с ним постоянным передаточным отношением. Приведенные моменты инерции звеньев первой группы – постоянны, их значение не зависит от положения механизма. Пусть их сумма обозначается} . Ко второй группе относятся все остальные звенья механизма. Приведенные моменты инерции звеньев этой группы – переменны, они зависят от положения механизма. Их сумма обозначается как _.

_{Следовательно,}

_{Определение: .}

_{Для нахождения используется метод приведения масс. В основу метода положено условие равенства кинетической энергии всех звеньев механизма и звена динамической модели. В этом случае закон движения последнего будет таким же, как и закон движения начального звена реального механизма. Для определения приведенного момента инерции каждого звена механизма необходимо составить равенство кинетических энергий рассматриваемого звена и звена модели.}

_{Приведенный момент инерции в общем виде определяется по формуле:}

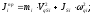
_{Где и - передаточные функции (аналоги скоростей).}

_{Для звеньев 2 и 3 значения были получены на ЭВМ}

_{Масштаб графика приведенных моментов инерции:}

Суммарный приведенный момент II группы звеньев:

1.4. Построение графика суммарной работы.

Суммарная работа всех сил равна работе _.

. График строим c помощью программа Maple 14.

Масштаб графика по оси ординат:

1.5 Определение угловой скорости звена приведения

График изменения угловой скорости имеет следующий вид. Численные значения следует брать из программы расчетов, выполненной в системе Maple 14.

Угловая скорость рассчитывается для третьего оборота.

Масштаб графика по оси ординат:

1.6 Определение углового ускорения звена приведения в функции обобщенной координаты

Для расчета углового ускорения звена приведения ε₁=f(φ₁) можно воспользоваться зависимостью:

Диаграмма углового ускорения строится с помощью программы Maple 14.

Масштаб графика по оси ординат:

1.7 Определение времени движения механизма

Время движения механизма определим по формуле:

График построен в программе Maple 14

Масштаб графика 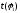по оси ординат:

Таблица результатов:

	0	30	60	90	120	150	180	210	240	270	300	330	360
№	0	1	2	3	4	5	6	7	8	9	10	11	12
JIIпр*102	1.1	1.7	2.6	2.65	1.98	1.33	1.1	1.33	1.98	2.65	2.6	1.7	1.1
Aсумм,Дж	0	89	100	48	-76	-314	-406	-231	-3	162	217	187	218
	41	41.2	41.24	41.1	40.8	40.1	39.9	40.5	41	41.4	41.56	41.5	41.6
	15.6	8.7	-5.16	-18.1	-34.2	-50.6	15.5	50.1	41.3	26.2	-9.3	1	15.6
t,c	0	0.013	0.025	0.038	0.051	0.064	0.077	0.090	0.105	0.117	0.13	0.141	0.153

2. Силовой расчет механизма.

2.1. Исходные данные.

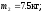
2.2. Построение плана скоростей.

Определим скорость точки A:

_М

Масштаб скоростей:

Звено 2 участвует в мгновенно-поступательном движении => V_A=V_B, V_AIIV_B

Тогда по теореме о проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки: V_A=V_B= V_S2=1,81м; ω₂=0.

2.3. Построение плана ускорений.

Определим ускорение точки В:

Определим угловое ускорение кривошипа с помощью программы Maple 14 при

Масштаб ускорений:

Определим ускорение точки B:

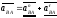
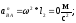
Определим ускорение точки S2:

Определим угловое ускорение шатуна при

2.3.1. Определение сил инерции, моментов сил инерции и сил тяжести.

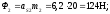
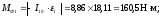
_{Определим массу присоединенного маховика:}

_{JM=7,7 кг*м2}

_{m=1230*(0,366*JM1/5)3=205 кг}

2.4. Определение сил в группе Ассура. Звенья 2-3

2.4.1. Нахождение силы .

;

;

2.4.2. Нахождение силы , _,.

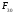F30=1170H;

F32n = F32=7010,6H;

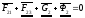
2.4.3. Нахождение силы .
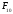