- •Расчетно-пояснительная
- •Содержание.
- •Определение закона движения механизма...................................6
- •2. Силовой расчет механизма.............................................................14
- •3. Проектирование цилиндрической эвольвентной зубчатой передачи и планетарного редуктора.....................................................................17
- •Техническое задание
- •Исходные данные
- •1. Проектирование механизма и определение закона его движения.
- •1.1. Проектирование механизма.
- •1.2.2. Построение графика силы
- •1.3. Выбор динамической модели и расчет ее параметров.
- •1.3.1. Вычисление значений передаточных функций.
- •1.3.2. Динамическая модель.
- •1.3.3. Приведение сил и построение графиков приведенных моментов.
- •1.3.4. Построение графика суммарного приведенного момента.
- •1.3.5. Построение переменных приведенных моментов инерции звеньев II группы
- •1.4. Построение графика суммарной работы.
- •1.5 Определение угловой скорости звена приведения
- •1.6 Определение углового ускорения звена приведения в функции обобщенной координаты
- •1.7 Определение времени движения механизма
- •2.5. Определение погрешности вычислений.
- •3.2. Идентификаторы, обозначения и наименования исходных и результирующих величин.
- •3.3. Выбор коэффициентов смещения.
- •3.4. Построение профиля зуба колеса, изготовляемого реечным инструментом.
- •3.5. Построение проектируемой зубчатой передачи.
- •3.6. Проектирование планетарного зубчатого механизма.
- •4. Проектирование кулачкового механизма.
- •4.1. Исходные данные и основные этапы проектирования.
- •4.3. Определение основных размеров кулачкового механизма.
- •Заключение:
- •Литература:
1.2.2. Построение графика силы
Функциональная зависимость, связывающая значение силы и кинематические параметры (время, координаты, скорость) точки приложения силы, называется механической характеристикой.
Для определения силы давления на поршень Fd необходимо давление умножить на площадь поршня. Знак силы устанавливается следующим образом: если сила совпадает по направлению с движением поршня, то она положительна, и наоборот.
Определим площадь поршня первой камеры:

 .
.
Определим площадь поршня второй камеры:

 .
.
1.3. Выбор динамической модели и расчет ее параметров.
1.3.1. Вычисление значений передаточных функций.
Положение звеньев механизма зависит лишь от его обобщенной координаты, поэтому для j-го звена и точки М этого звена можно записать:


Где
 - угол поворота j-го
звена (рассматривается плоское движение),
- угол поворота j-го
звена (рассматривается плоское движение),
 - радиус –вектор точки М в выбранной
системе координат. Эти функции называются
функциями положения. Производные от
- радиус –вектор точки М в выбранной
системе координат. Эти функции называются
функциями положения. Производные от
 и
и
 по обобщенной координате носят названия
аналогов скоростей и ускорений
(кинематические передаточные функции).
по обобщенной координате носят названия
аналогов скоростей и ускорений
(кинематические передаточные функции).
Для нахождения передаточных функций и передаточных отношений основного механизма, был использован метод векторных контуров.
В результате проецирования векторного контура получаем следующие соотношения для передаточных функций.


Масштабы графиков аналогов:


1.3.2. Динамическая модель.
Динамической
моделью машины называется отдельно
взятое звено приведения, образующее
вращательную пару со стойкой, условно
снабженное переменным моментом
вращающееся под действием момента .
Если приведенные параметры
.
Если приведенные параметры
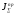 и
и
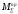 определены для машины по условиям
приведения, то движение динамической
модели тождественно истинному движению
главного вала в составе машины, так как
эти движения описываются одним и тем
же уравнением. Величины
определены для машины по условиям
приведения, то движение динамической
модели тождественно истинному движению
главного вала в составе машины, так как
эти движения описываются одним и тем
же уравнением. Величины
 и
и
 называют параметрами динамической
модели.
называют параметрами динамической
модели.
Таким образом, задача о движении многозвенного механизма сведена к рассмотрению движения одного условного звена – динамической модели машины.
1.3.3. Приведение сил и построение графиков приведенных моментов.
Закон движения механизма определяется характером сил и моментов, приложенных к его звеньям. Все внешние силы, действующие на машину, делятся на движущие силы Fд (момент движущих сил Мд) и силы сопротивления Fc (момент сил сопротивления Mc).
Движущими
называются силы, которые совершают
положительную работу. Это происходит
в том случае, если скалярное произведение
Fд ,
то есть положительно (
,
то есть положительно ( -
скорость точки приложения силы).
-
скорость точки приложения силы).
Работа
сил сопротивления за цикл отрицательны,
и скалярное произведение Fд .
.
Суммарный приведенный момент:
 .
.
Приведенный
момент сил сопротивления
 определяем
в каждом положении механизма по формуле:
определяем
в каждом положении механизма по формуле: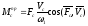 .
Знак
.
Знак
 определяется
знаком
определяется
знаком
 .
Значение
.
Значение
 .
.
Масштаб
по оси ординат графика
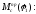

Масштаб
по оси абсцисс

Приведенным
моментом
 от
силы тяжести
от
силы тяжести
 звена
2 пренебрегаем, так как он мал.
звена
2 пренебрегаем, так как он мал.
|
|
0 |
30 |
60 |
90 |
120 |
150 |
180 |
|
№ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Vqc, м/рад |
0 |
|
-0.0429 |
-0.044 |
-0.0332 |
-0.021 |
0 |
|
Fс, Н |
0 |
1679 |
4052 |
6945 |
13658 |
27210 |
27210 |
|
Mс, Нм |
0 |
-45 |
-174 |
-306 |
-454 |
-592 |
0 |
|
|
210 |
240 |
270 |
300 |
330 |
330 |
|
№ |
7 |
8 |
9 |
10 |
11 |
12 |
|
Vqc, м/рад |
0.017 |
0.033 |
0.044 |
0.0429 |
0.0268 |
0 |
|
Fс, Н |
18242 |
7256 |
2306 |
-5366 |
-5424 |
0 |
|
Mс, Нм |
314 |
241 |
102 |
-231 |
-145 |
0 |