
- •Практическое занятие 2. Предел числовой последовательности
- •Теоретический диктант.
- •Решение типовых задач.
- •Решение типовых задач.
- •Практическое занятие 4. Преобразование графиков функций.
- •Решение типовых задач.
- •Практическое занятие 5. Предел функции.
- •Решение типовых задач.
- •Теоретический диктант.
- •Решение типовых задач.
- •Практическое занятие 10. Геометрический смысл производной. Касательная к графику функции.
- •Решение типовых задач.
- •Решение типовых задач.
- •Решение типовых задач.
ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
ПО
МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
для студентов 1 курса группы ЭОО 11/1
направления «Экономика»
2011-2012 уч.год
Преподаватель: Корпачева М.А.
Практическое занятие 1.
Действительные числа.
Числовые последовательности.
Контрольные вопросы:
-
Числовые множества.
-
Модуль числа.
-
Числовая последовательность.
-
Произведение последовательности на число.
-
Сумма последовательностей.
-
Разность последовательностей.
-
Произведение последовательностей.
-
Частное последовательностей.
-
Арифметическая прогрессия.
-
Формулы для n-го члена арифметической прогрессии.
-
Формула суммы n первых членов арифметической прогрессии.
-
Геометрическая прогрессия.
-
Формулы для n-го члена геометрической прогрессии.
-
Формула суммы n первых членов геометрической прогрессии.
План занятия:
-
Теоретический диктант.
Номер задания
Аудиторная работа
Домашняя работа
1
а
б
2
в
а, б
3
б, г, е
а, в, д
4
а, г
б, в
5
а, в,
б, г
6
-
+
7
а, д
б, в, г
8
а, в
б, г
9
а
б
10
+
11
-
+
12
+
-
13
-
+
14
-
+
15
+
-
-
Решение типовых задач.
Задание 1.
а) Пусть множество
![]() состоит из юношей данной группы, а
состоит из юношей данной группы, а
![]() - из девушек той же группы. Найти
- из девушек той же группы. Найти
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
б) Пусть
![]() ℕ
ℕ
![]() ℕ
ℕ![]() ,
,
![]() ℕ
ℕ![]() ℕ
ℕ![]() .
Найти
.
Найти
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Задание 2. Даны множества
![]() и
и
![]() .
Найти
.
Найти
![]() ,
,
![]() ,
,
![]() ,
,
![]() :
:
а)
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() ;
;
в)
![]() ,
,
![]() .
.
Задание 3. Отметьте на координатной прямой множества:
а)
![]() ℕ
ℕ
![]() ;
;
б)
![]() ℤ
ℤ
![]() ;
;
в)
![]() ℝ
ℝ
![]() ;
;
г)
![]() ℝ
ℝ
![]() ;
;
д)
![]() ℝ
ℝ
![]() ;
;
е)
![]() ℝ
ℝ
![]() .
.
Задание 4. Отметьте на координатной плоскости множества точек, координаты которых удовлетворяют неравенству:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Задание 5. Определить множества
значений
![]() ,
удовлетворяющих условию:
,
удовлетворяющих условию:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Задание 6. найти модуль числа:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Задание 7. Дана формула общего члена последовательности. Написать пять первых элементов последовательности:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
Задание 8. Зная несколько первых членов последовательности, написать формулу общего элемента этой последовательности:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Задание 9. Написать пять первых членов и формулу общего элемента последовательности:
а)
![]() ;
;
б)
![]() .
.
Задание 10. Сумма трех первых членов возрастающей арифметической прогрессии равна 21. Если от первых двух членов этой прогрессии отнять по 1, а к третьему прибавить 2, то полученные 3 числа составят геометрическую прогрессию. Найти сумму восьми первых членов геометрической прогрессии.
Задание 11. Найти сумму первых шести членов арифметической прогрессии, у которой сумма любого числа членов равна учетверенному квадрату этого числа.
Задание 12. Известно, что при любом
![]() сумма
сумма
![]() первых членов некоторой числовой
последовательности
первых членов некоторой числовой
последовательности
![]() выражается формулой
выражается формулой
![]() .
Найти девятый член этой последовательности
и доказать, что
.
Найти девятый член этой последовательности
и доказать, что
![]() является арифметической прогрессией.
является арифметической прогрессией.
Задание 13. Сумма третьего и девятого членов арифметической прогрессии равна 8. Найти сумму первых 11 членов этой прогрессии.
Задание 14. В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах – одно штрафное очко, а за каждый последующий – на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, если он получил 7 штрафных очков?
Задание 15. Найти число членов конечной геометрической прогрессии, у которой первый, второй и последний члены равны соответственно 3, 12 и 3072.
Практическое занятие 2. Предел числовой последовательности
Контрольные вопросы:
-
Бесконечно большая последовательность.
-
Бесконечно малой последовательность.
-
Теоремы о бесконечно малых последовательностях.
-
Сходящаяся последовательность.
-
Расходящаяся последовательность.
-
Свойства сходящихся последовательностей.
-
Число
 .
.
План занятия:
-
Теоретический диктант.
-
Проверка домашнего задания.
-
Решение типовых задач.
|
Номер задания |
Аудиторная работа |
Домашняя работа |
|
1 |
1,2,5,7,10,13,15,16,19-22 |
3,4,6,8,9,11,12,14,17,18,23-25 |
|
2 |
1,4,5,7 |
2,3,6 |
Задание 1. Найти предел:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() ;
;
15) ![]() ;
;
16) ![]() ;
;
17) ![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]() ;
;
21)
![]() ;
;
22)
![]() ;
;
23)
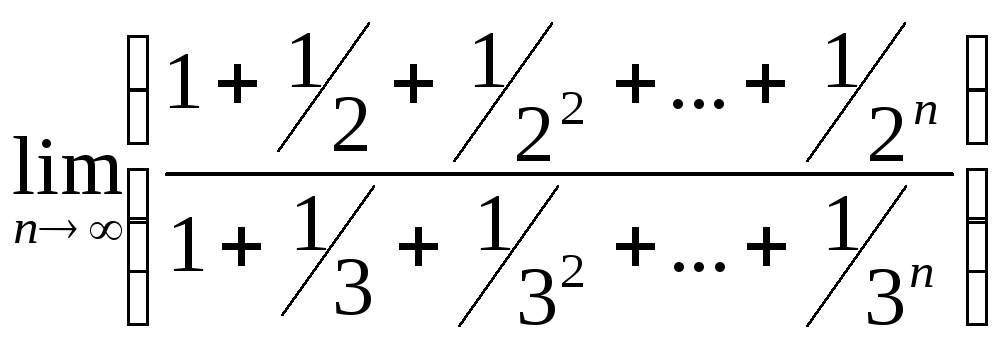 ;
;
24)
![]() ;
;
25)
![]() .
.
Задание 2. Найти предел:
1) ![]() ;
5)
;
5)
![]() ;
;
2) ![]() ; 6)
; 6)
![]() ;
;
3) ![]() ; 7)
; 7)
![]() .
.
4) ![]() ;
;
Практическое занятие 3.
Понятие функции.
Область определения функции.
Основные элементарные функции.
Контрольные вопросы:
-
Понятие функции.
-
Область определения функции.
-
Область значений функции.
-
Постоянная функция.
-
Четная функция.
-
Нечетная функция.
-
Периодическая функция.
-
Возрастающая функция.
-
Убывающая функция.
-
Обратная функция.
-
Композиция (суперпозиция) функций.
-
Основные элементарные функции, их свойства и графики.
-
Классификация элементарных функций.
План занятия:
-
Самостоятельная работа (вычисление пределов числовой последовательности).
-
Проверка домашнего задания.
-
Решение типовых задач.
|
Номер задания |
Аудиторная работа |
Домашняя работа |
|
1 |
1,4,5 |
2,3 |
|
2 |
2,4,6 |
1,3,5 |
|
3 |
1,4 |
2,3 |
|
4 |
3,4,5 |
1,2 |
|
5 |
2,5,6 |
1,3,4 |
|
6 |
1,4 |
2,3 |
|
7 |
1,3,7,8,10,13,15 |
2,4-6,9,11,12,14 |
|
8 |
1,3,6 |
2,4,5 |
Задание 1. Следующие сложные функции представить с помощью цепочек, составленных из основных элементарных функций:
-
 ;
; -
 ;
; -
 ;
; -
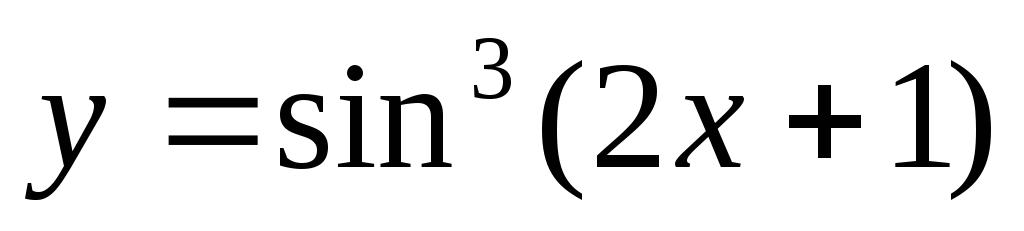 ;
; -
 .
.
Задание 2. Написать в явном виде
функцию
![]() ,
неявно заданную уравнением:
,
неявно заданную уравнением:
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 .
.
Задание 3. Тождественны ли функции:
-
 и
и
 ;
; -
 и
и
 ;
; -
 и
и
 ;
; -
 и
и
 .
.
Задание 4. Найти интервалы знакопостоянства функции:
-
 ;
; -
 ;
; -
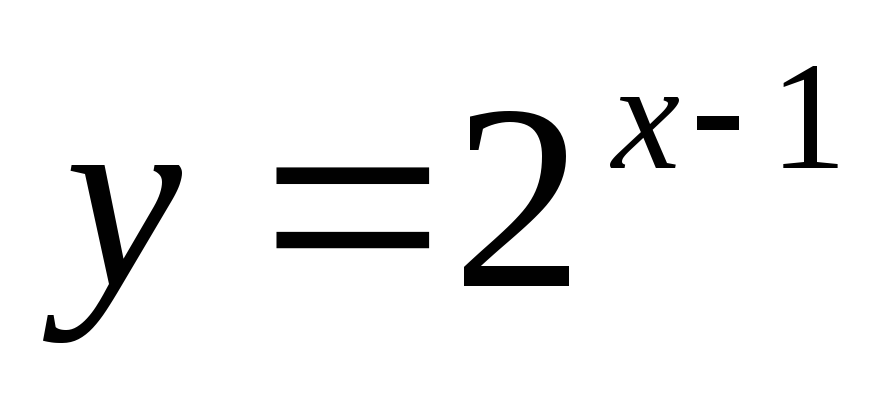 ;
; -
 ;
; -
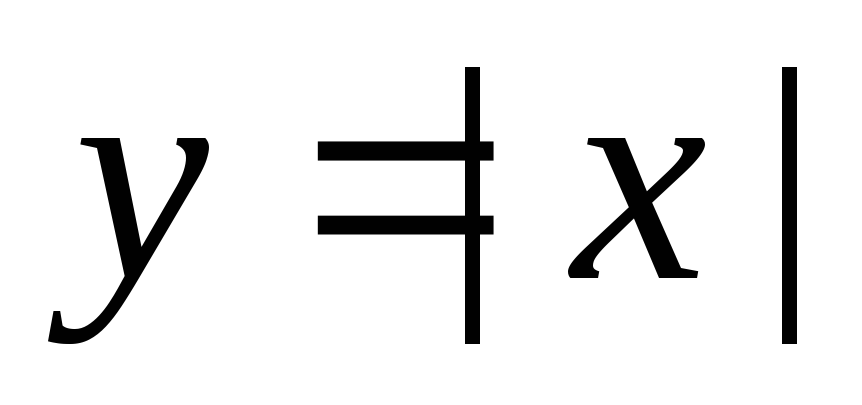 .
.
Задание 5. Исследовать на четность, нечетность функцию:
-
 ;
; -
 ;
; -
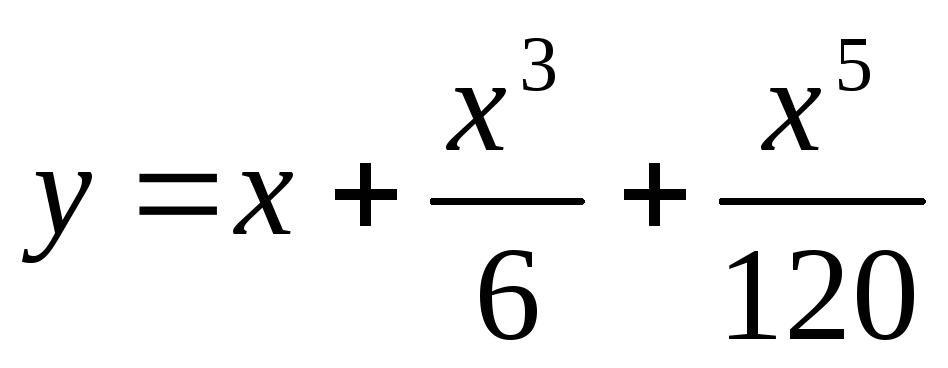 ;
; -
 ;
; -
 ;
; -
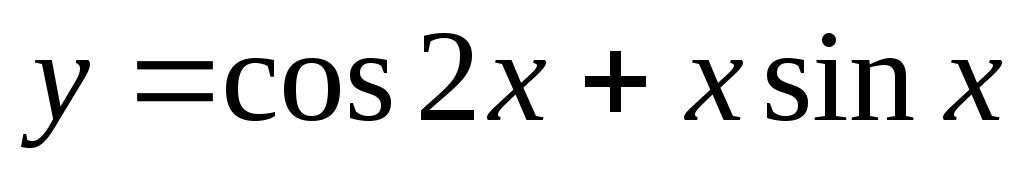 .
.
Задание 6. Доказать, что:
-
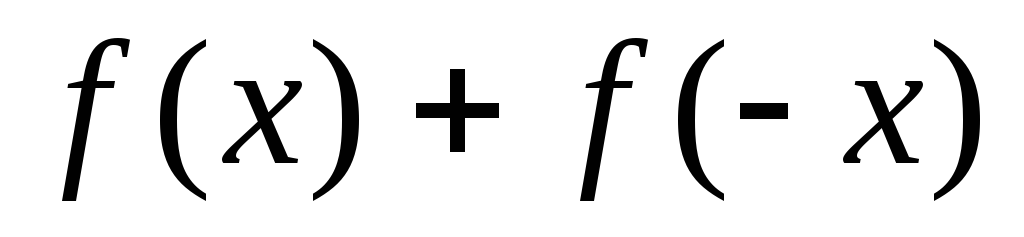 - четная функция, а
- четная функция, а
 - нечетная;
- нечетная; -
произведение двух четных функций – четная функция;
-
произведение двух нечетных функций – четная функция;
-
произведение четной и нечетной функций – нечетная функция.
Задание 7. Найти область определения функции:
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 .
.
Задание 8. Найдите множества значений функции:
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
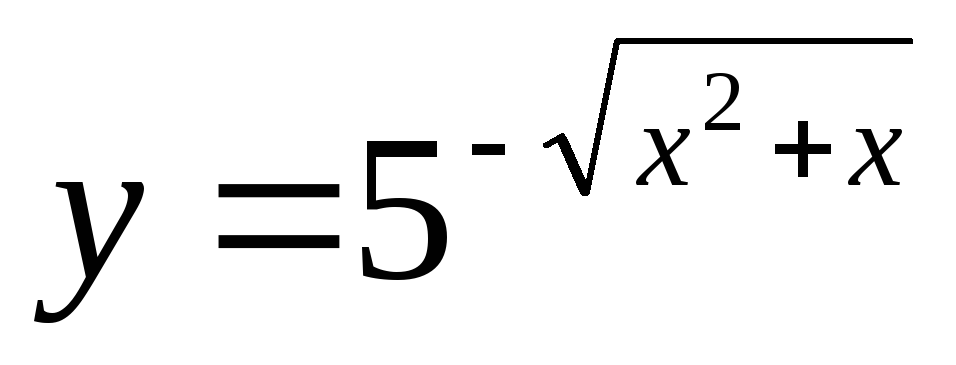 ;
; -
 ;
; -
 ;
; -
 .
.
