
- •Введение. Основные понятия и термины
- •Классификации систем автоматического регулирования
- •Дифференциальные уравнения линейных сар
- •Передаточные функции
- •Передаточные функции линейных сар
- •Преобразования структурных схем
- •Характеристики замкнутых сар и процессы в них
- •Типовые звенья
- •Статические и астатические сар
- •Устойчивость сар Понятие устойчивости
- •Алгебраические критерии устойчивости
- •Частотные критерии устойчивости
- •Оценка качества работы сар Показатели качества работы сар
- •Оценка точности работы сар в установившихся режимах
- •Оценка качества переходных процессов
- •Оценка качества работы сар по резонансному максимуму ачх замкнутой системы
- •Синтез сар
- •Синтез систем с последовательной коррекцией
- •Синтез сар из условия минимума резонансного максимума ачх замкнутой системы
- •Вопросы синтеза параллельных корректирующих звеньев
- •Системы подчиненного регулирования Общие принципы построения систем подчиненного регулирования
- •Оптимизация спр по модульному оптимуму
- •Оптимизация двухконтурной системы регулирования скорости двигателя постоянного тока независимого возбуждения
- •Оптимизация двукратноинтегрирующих спр. Симметричный оптимум
- •Инвариантные сар
Типовые звенья
Любая САР может быть представлена в виде комбинации (последовательного или параллельного соединения) типовых звеньев. К числу типовых звеньев, из которых состоят линейные САР, относятся следующие звенья с ПФ:
1. Усилительное
звено
![]()
2. Интегрирующее
звено
![]()
3. Дифференцирующее
звено
![]()
4. Апериодическое
звено
![]()
5. Форсирующее
звено 1-го порядка
![]()
6. Колебательное
звено
![]() ,
,
![]()
7. Форсирующее
звено 2-го порядка
![]()
8. Звено чистого
запаздывания
![]()
Усилительное звено (усилитель)
![]()
![]() – коэффициент передачи
– коэффициент передачи
![]()
Д![]() ифференциальное
уравнение
ифференциальное
уравнение
![]() .
.
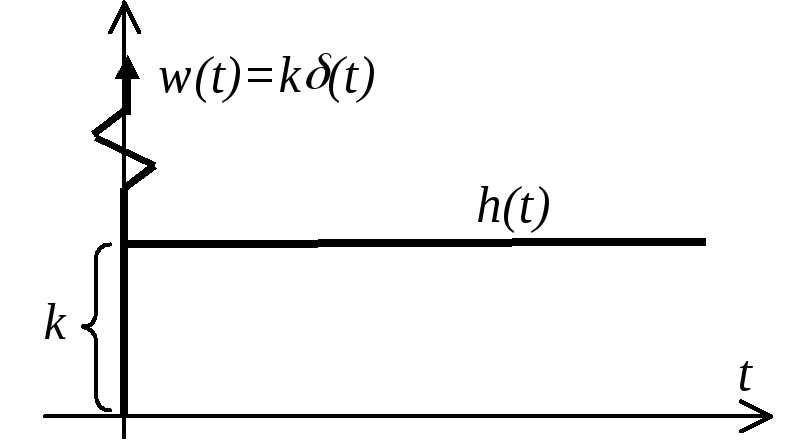
Переходная функция (см. рисунок)
![]() .
.
Весовая функция (см. рисунок)
![]() .
.
Частотная характеристика
![]() .
.
А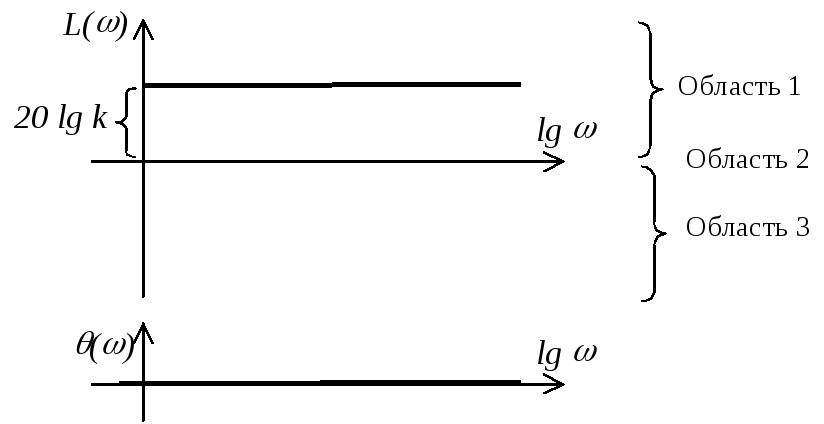 ЧХ
ЧХ
![]() .
.
ФЧХ и ЛФЧХ
![]() .
.
ЛАЧХ
![]() .
.
Область 1 – при
![]()
Область 2 – при
![]()
Область 3 – при
![]()
Интегрирующее звено (интегратор)
![]()
![]() – коэффициент
передачи;
– коэффициент
передачи;
![]() – постоянная времени.
– постоянная времени.
![]()
Д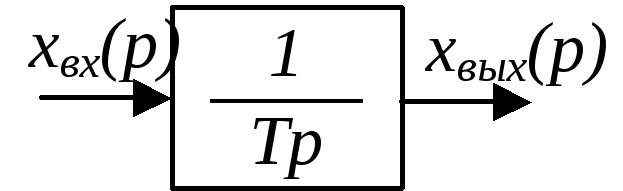 ифференциальное
уравнение
ифференциальное
уравнение
![]() .
.
П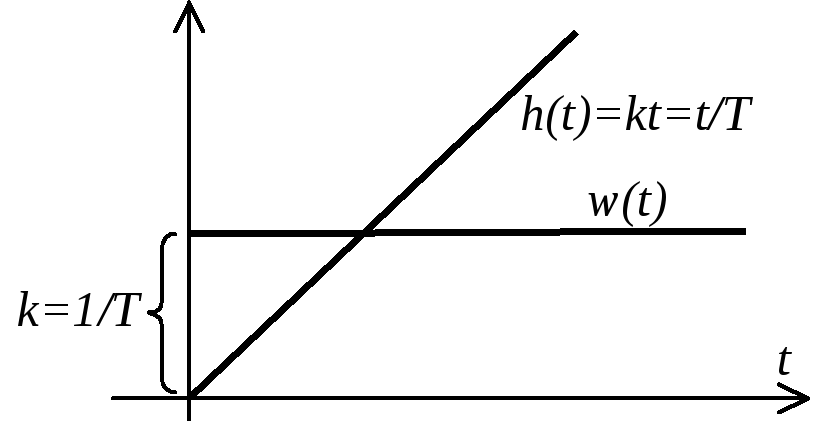 ереходная
функция (см. рисунок)
ереходная
функция (см. рисунок)
![]() .
.
Весовая функция (см. рисунок)
![]() .
.
Применительно к нашей специальности
для интегратора чаще используется
понятие постоянной времени
![]() .
.
При наличии на входе интегратора постоянного сигнала, отличного от нуля, сигнал на его выходе изменяется по линейному закону, при равенстве сигнала на входе нулю сигнал на выходе интегратора стабилизируется и в общем случае отличен от нуля.
Частотная
характеристика ![]() .
.
АЧХ ![]() .
.
ФЧХ ![]() .
.
Таким образом, в интеграторе выходной сигнал отстает от входного по фазе на /2, независимо от частоты .
ЛАЧХ ![]() .
.
ЛФЧХ ![]() .
.
ЛАЧХ при какой-то определенной частоте 1 равна L(1)= –20 lg 1T. При увеличении частоты в 10 раз (на одну декаду) L(101) = –20 lg 101T = –20 lg 1T – 20. Поскольку L(1) – L(101) = 20 дБ, следовательно, ЛАЧХ интегрирующего звена представляет собой прямую с наклоном –20 дБ/дек.
Построение ЛАЧХ производим по характерным точкам (см. рисунок):
-
при =1 L()= –20 lg T = 20 lg 1/T = 20 lg k.
-
при =1/T L()=0.
Наклон ЛАЧХ –20 дБ/дек соответствует наклону АЧХ –1, поэтому его часто так и обозначают.
Как уже отмечалось, ЛФЧХ не зависит от частоты и представляет собой прямую на уровне –/2.
П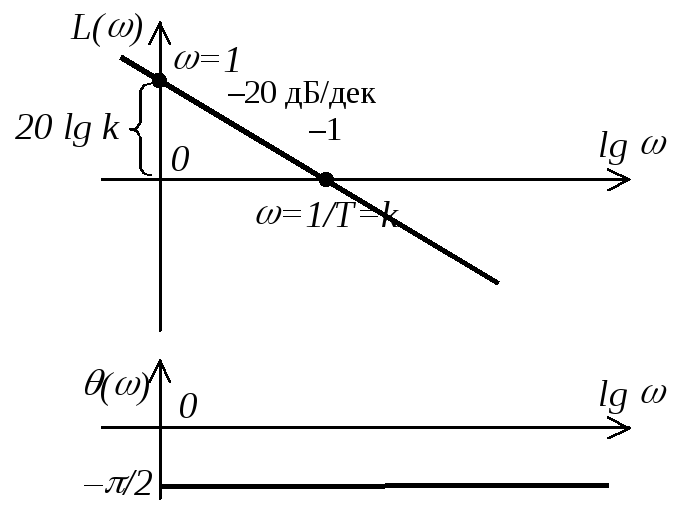 ри
ри
![]() ,
как следует из АЧХ и ЛАЧХ, коэффициент
передачи интегратора по амплитуде
стремится к бесконечности; и напротив,
при увеличении частоты коэффициент
передачи по амплитуде уменьшается. Это
означает, что интегратор не пропускает
на выход высокие частоты, являясь
фильтром
низких частот.
,
как следует из АЧХ и ЛАЧХ, коэффициент
передачи интегратора по амплитуде
стремится к бесконечности; и напротив,
при увеличении частоты коэффициент
передачи по амплитуде уменьшается. Это
означает, что интегратор не пропускает
на выход высокие частоты, являясь
фильтром
низких частот.
Дифференцирующее звено (дифференциатор)
![]()
![]() – постоянная
времени
– постоянная
времени
![]()
Д![]() ифференциальное
уравнение
ифференциальное
уравнение
![]() .
.
П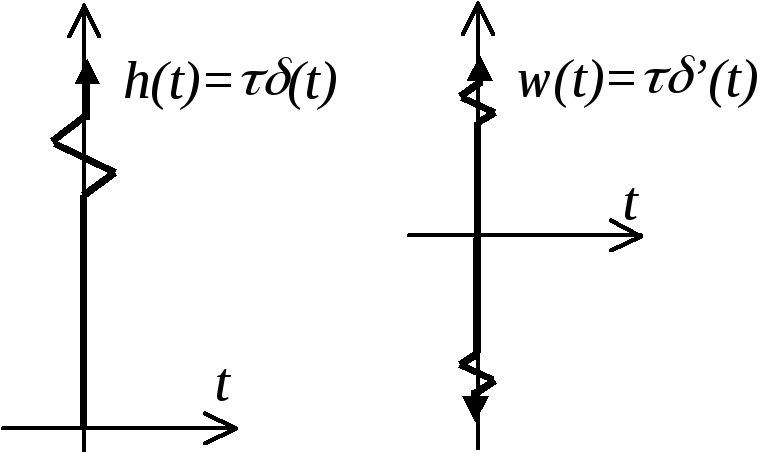 ереходная
функция (см. рисунок)
ереходная
функция (см. рисунок)
![]() .
.
Весовая функция (см. рисунок)
![]() .
.
Частотная
характеристика ![]() .
.
АЧХ ![]() .
.
ФЧХ ![]() .
.
Таким образом, в дифференциаторе выходной сигнал опережает входной по фазе на /2, независимо от частоты .
ЛАЧХ ![]() .
.
ЛФЧХ ![]() .
.
Аналогично тому,
как это было сделано для интегратора,
можно показать, что ЛАЧХ дифференцирующего
звена представляет собой прямую с
наклоном +20 дБ/дек (+1), которая будет
пересекать ось частот при
![]() (см. рисунок).
(см. рисунок).
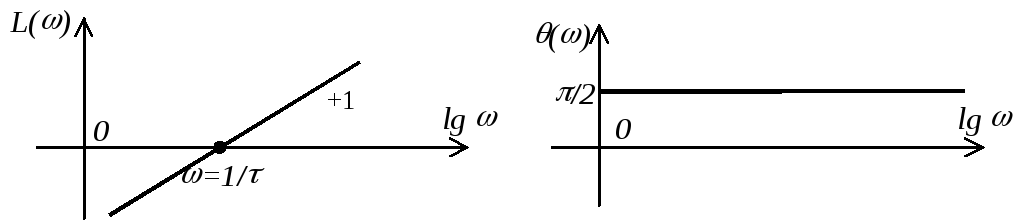
Из ЛАЧХ видно, что с ростом увеличивается коэффициент передачи дифференциатора по амплитуде. Таким образом, данное звено является помехонеустойчивым в том смысле, что оно подчеркивает высокочастотные помехи (наиболее частые на практике): даже при малой входной амплитуде высокочастотного сигнала на выходе можно наблюдать значительную высокочастотную составляющую.
Примечание.
ПФ дифференцирующего звена является
обратной по отношению к передаточной
функции интегрирующего звена. Кроме
того (точнее, следовательно), ЛАЧХ и ЛФЧХ
дифференциатора являются зеркальными
отображениями соответствующих
характеристик интегратора относительно
оси частот. На основании этого можно
сделать более широкий вывод:
логарифмические частотные характеристики
любого звена с ПФ
![]() являются обратными соответствующим
характеристикам звена с ПФ
являются обратными соответствующим
характеристикам звена с ПФ
![]() ,
то есть, являются их зеркальными
отображениями относительно оси частот
.
,
то есть, являются их зеркальными
отображениями относительно оси частот
.
Апериодическое звено (инерционное)
![]()
![]() – коэффициент
передачи;
– коэффициент
передачи;
![]() – постоянная времени
– постоянная времени
![]()
Д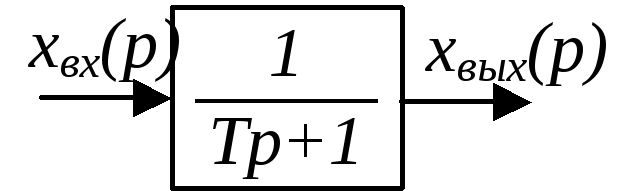 ифференциальное
уравнение
ифференциальное
уравнение
![]() .
.
Найдем сначала
импульсную переходную функцию, зная ее
связь с ПФ и используя теорему разложения.
ПФ содержит один полюс
![]() ,
следовательно,
,
следовательно,
![]() ,
,
![]()
и
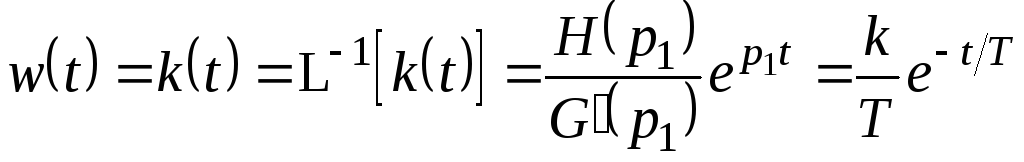 .
.
Переходная функция (см. рисунок)
![]() .
.
И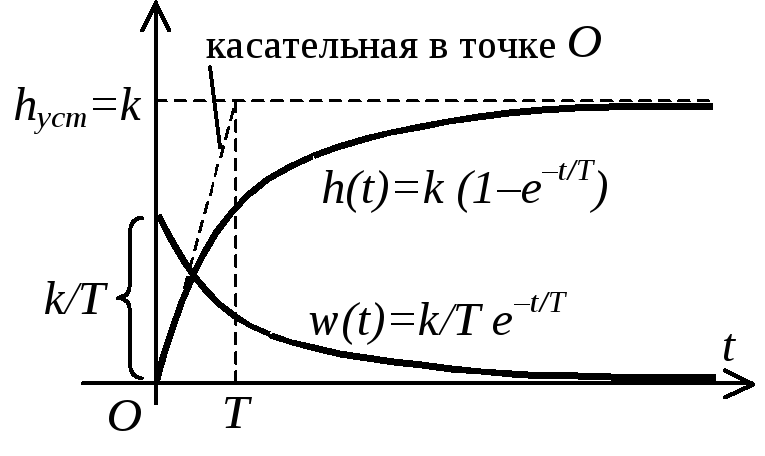 спользуя
выражение для переходной функции, можно
определить:
спользуя
выражение для переходной функции, можно
определить:
h(T) = 0,632 k = 0,632 hуст
h(2T) = 0,865 hуст
h(3T) = 0,950 hуст
h(4T) = 0,982 hуст
Таким образом,
переходный процесс практически закончится
при
![]() .
.
Постоянная времени T является мерою инерционности апериодического звена. Чем меньше значение Т, тем быстрее протекает переходный процесс.
Частотная характеристика
![]() .
.
АЧХ ![]() .
.
ФЧХ ![]() .
.
Таким образом, в апериодическом звене фазовый сдвиг зависит от частоты, причем максимальный фазовый сдвиг будет равен –/2 при .
ЛАЧХ ![]() .
.
ЛФЧХ ![]() .
.
Логарифмические частотные характеристики (ЛЧХ) усилительного, интегрирующего и дифференциального звеньев являются прямыми линиями, и легко могут быть построены. Построение ЛЧХ апериодического и остальных звеньев требует вычислений, которые без использования ЭВМ достаточно трудоемки. Поэтому в большинстве случаев на практике ограничиваются построением приближенных асимптотических ЛЧХ, на основании которых уже могут быть сделаны все основные выводы о динамических свойствах звена.
Рассмотрим алгоритм построения асимптотических ЛАЧХ и ЛФЧХ апериодического звена.
Асимптотическая
ЛАЧХ. При
малых частотах
![]() второе слагаемое под радикалом
второе слагаемое под радикалом
![]() ,
и им можно пренебречь; тогда
,
и им можно пренебречь; тогда
![]() .
При больших частотах
.
При больших частотах
![]() под радикалом можно пренебречь единицей
по сравнению с
под радикалом можно пренебречь единицей
по сравнению с
![]() ,
и тогда
,
и тогда
![]() .
Таким образом, асимптотическая ЛАЧХ
состоит из двух отрезков, пересекающихся
на оси частот в точке, соответствующей
частоте
.
Таким образом, асимптотическая ЛАЧХ
состоит из двух отрезков, пересекающихся
на оси частот в точке, соответствующей
частоте
![]() ,
называемой частотой
сопряжения
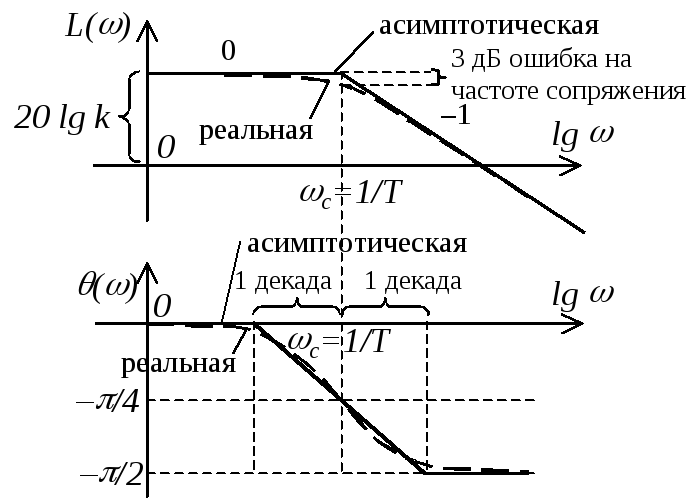
(см. рисунок). Реальная ЛАЧХ апериодического
звена (показана пунктиром) имеет
максимальное отличие от асимптотической
(3 дБ) при частоте сопряжения.
,
называемой частотой
сопряжения
(см. рисунок). Реальная ЛАЧХ апериодического
звена (показана пунктиром) имеет
максимальное отличие от асимптотической
(3 дБ) при частоте сопряжения.
Асимптотическая
ЛФЧХ. При
частоте сопряжения
![]()
![]() .
При малых
.
При малых
![]()
![]() ,
а при больших
,
а при больших
![]()
![]() .
На практике при частотах, близких к
частоте сопряжения (1
декада) ЛФЧХ может без большой погрешности
заменена линейной зависимостью,
проходящей через точку
.
На практике при частотах, близких к
частоте сопряжения (1
декада) ЛФЧХ может без большой погрешности
заменена линейной зависимостью,
проходящей через точку
![]() (см. рисунок).
(см. рисунок).
Форсирующее звено 1-го порядка
![]()
![]() – постоянная
времени
– постоянная
времени
![]()
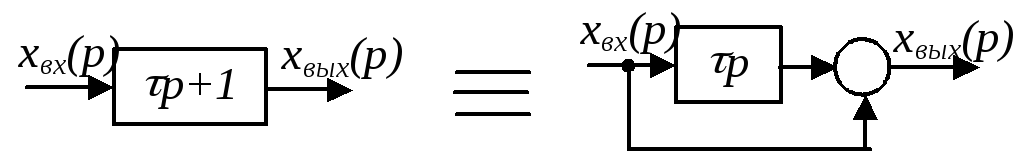
Из эквивалентной схемы видно, что это звено подает на выход входной сигнал и его производную.
Дифференциальное уравнение
![]() .
.
П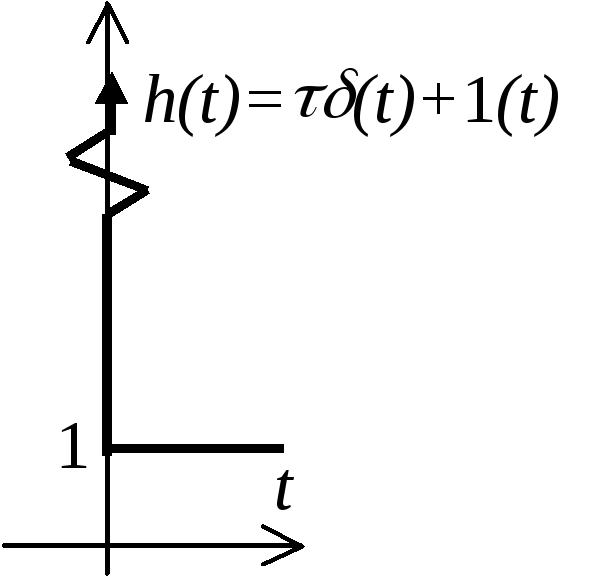 ереходная
функция (см. рисунок)
ереходная
функция (см. рисунок)
![]() .
.
Весовая функция:
![]() .
.
Частотная характеристика
![]() .
.
АЧХ ![]() .
.
ФЧХ ![]() .
.
Как и дифференцирующее звено, форсирующее звено 1-го порядка является помехонеустойчивым, поскольку усиливает высокочастотные составляющие входного сигнала.
ЛАЧХ ![]() .
.
ЛФЧХ ![]() .
.
П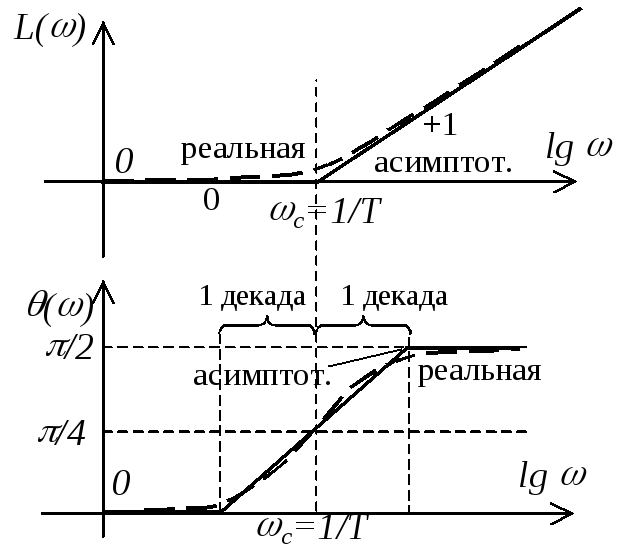 оскольку
ПФ форсирующего звена 1-го порядка
обратна ПФ апериодического звена (при
k=1),
то ЛЧХ форсирующего звена являются
зеркальным отображением относительно
оси частот соответствующих характеристик
апериодического звена при k=1
(см. рисунок).
оскольку
ПФ форсирующего звена 1-го порядка
обратна ПФ апериодического звена (при
k=1),
то ЛЧХ форсирующего звена являются
зеркальным отображением относительно
оси частот соответствующих характеристик
апериодического звена при k=1
(см. рисунок).
Колебательное звено
![]()
![]() – коэффициент
передачи;
– коэффициент
передачи;
![]() – постоянная времени
– постоянная времени
![]()
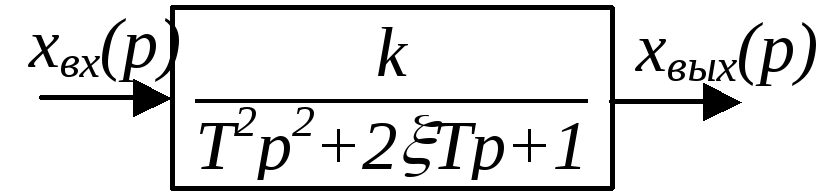
Иногда используют другую форму записи ПФ колебательного звена:
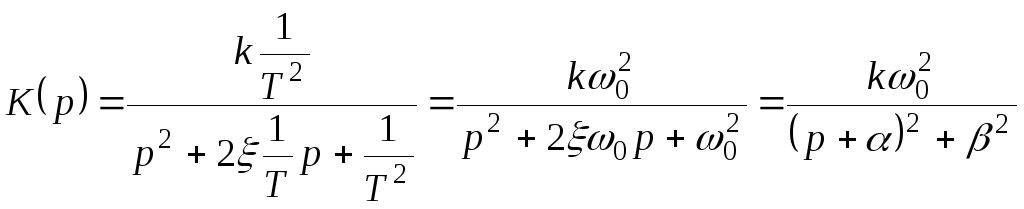 ,
,
где 0<<1 – коэффициент демпфирования;
![]() – угловая частота
колебательного звена;
– угловая частота
колебательного звена;
, – модули действительной и мнимой частей полюсов ПФ колебательного звена.
Доказательство. Корни уравнения
![]() равны
равны
![]() ,
поскольку
,
поскольку
![]() .
.
Для определения коэффициентов , приравняем знаменатели первого и последнего выражений для ПФ:
![]() .
.
Приравнивая коэффициенты при одинаковых степенях p, можно найти:
![]() ;
;
![]() ;
;
![]() .
.
Дифференциальное уравнение:
![]() .
.
Выражения для переходной и весовой функций могут быть выведены с помощью обратного преобразования Лапласа с использованием теоремы разложения при комплексных корнях (примите без доказательства).
Вывод выражения для переходной функции:
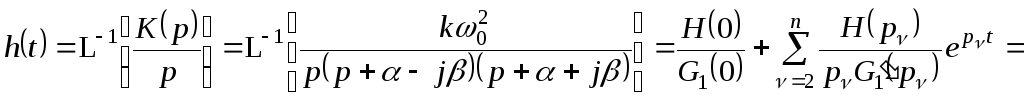
![]()
![]()
![]()
![]()
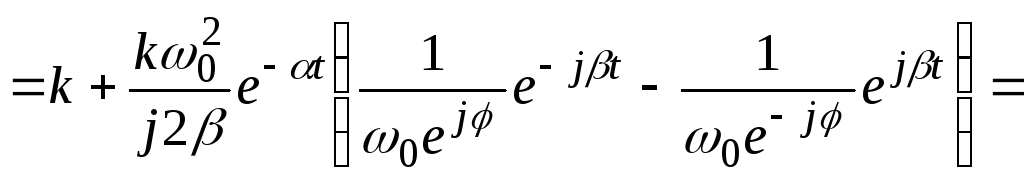
![]()
![]()
![]() .
.
Вывод выражения для весовой функции:
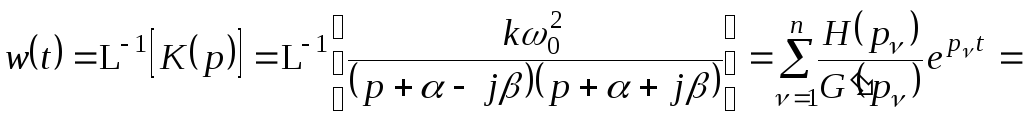
![]()
![]()
![]()
![]() .
.
Переходная функция (см. рисунок)
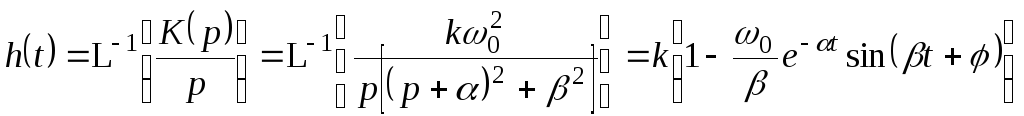 ,
,
г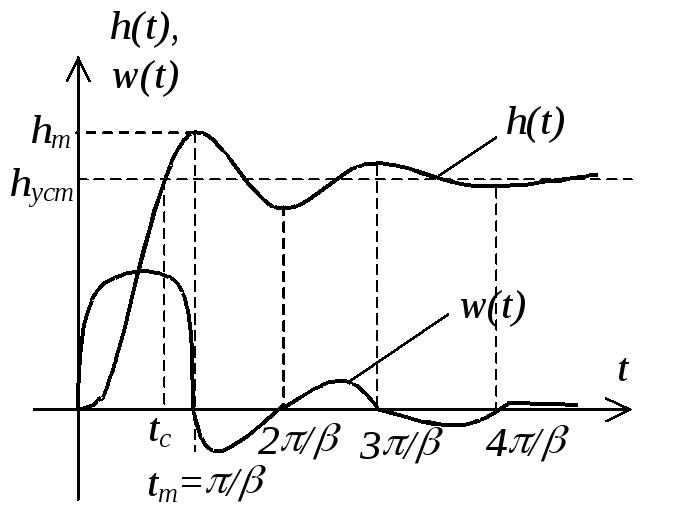 де
де
![]() .
.
Весовая функция (см. рисунок)
![]() .
.
Установившееся значение:
hуст = k
Значение времени
первого согласования tc
можно узнать, если в выражении для
переходной функции приравнять синус
нулю, тогда
![]() ,
отсюда
,
отсюда
![]() .
.
Время tm достижения максимального значения можно узнать, приравняв значение весовой функции нулю:
![]() .
.
Равенство нулю
весовой функции будет иметь место также
для всех
![]() ,
где
,
где
![]() – положительное целое число (см. рисунок).
– положительное целое число (см. рисунок).
Подставив tm в выражение для переходной функции, определим максимальное значение выходной переменной в переходном режиме:
![]() ,
,
где
![]() .
.
Наконец, перерегулирование
![]() .
.
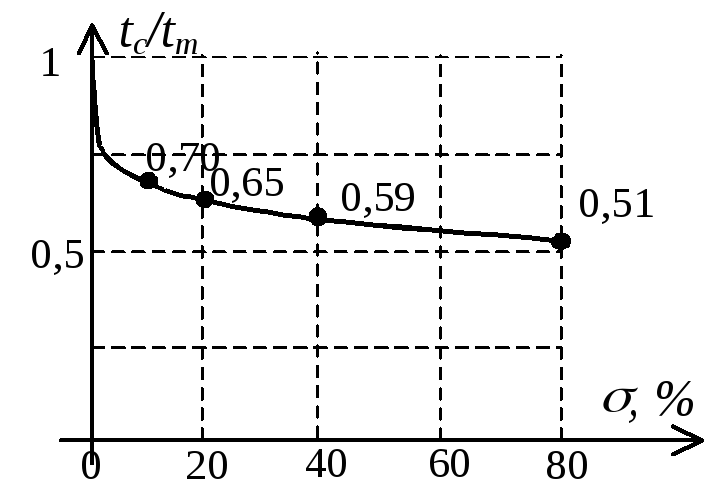
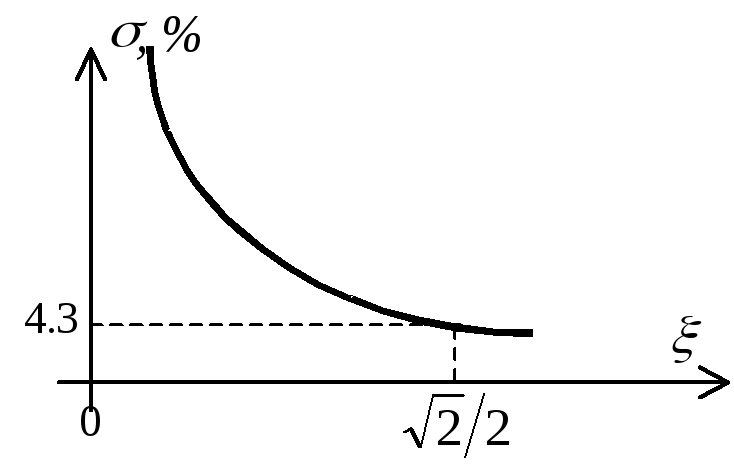
Известны
соответствующие графики зависимостей
[3]
![]() и
и
![]() :
:
Частотная характеристика:
![]() .
.
АЧХ ![]() .
.
ФЧХ ![]() .
.
ЛАЧХ ![]() .
.
ЛФЧХ ![]() .
.
Асимптотическая
ЛАЧХ. При
малых частотах
![]() можно пренебречь составляющей
можно пренебречь составляющей
![]() ,
тогда
,
тогда
![]() .
При больших частотах
.
При больших частотах
![]() под радикалом можно пренебречь единицей
по сравнению с
под радикалом можно пренебречь единицей
по сравнению с
![]() ,
и тогда
,
и тогда
![]() .
.
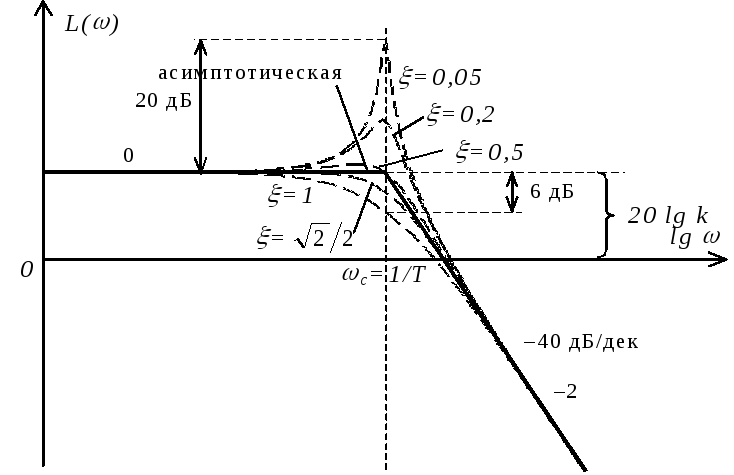
Таким образом,
асимптотическая ЛАЧХ колебательного
звена состоит из двух отрезков,
пересекающихся на оси частот в точке,
соответствующей частоте сопряжения
![]() (см. рисунок). Реальная ЛАЧХ достаточна
близка к асимптотической (погрешность
на частоте сопряжения не превышает 6
дБ) при =0,2…1,0.
В остальных случаях (когда 0,2)
следует воспользоваться либо кривыми
поправок [1], либо точным математическим
выражением для ЛАЧХ.
(см. рисунок). Реальная ЛАЧХ достаточна
близка к асимптотической (погрешность
на частоте сопряжения не превышает 6
дБ) при =0,2…1,0.
В остальных случаях (когда 0,2)
следует воспользоваться либо кривыми
поправок [1], либо точным математическим
выражением для ЛАЧХ.
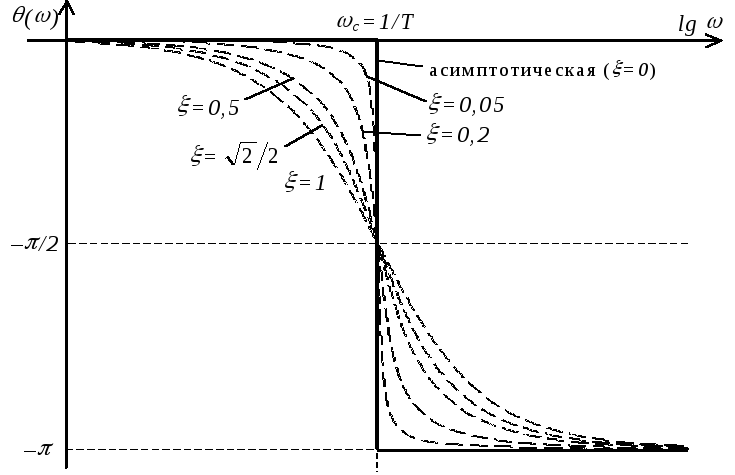
Асимптотическая
ЛФЧХ. При
частоте сопряжения
![]()
![]() .
При малых
.
При малых
![]()
![]() ,
а при больших
,
а при больших
![]()
![]() .
Но асимптотическая ЛФЧХ совпадает с
реальной только при
.
Но асимптотическая ЛФЧХ совпадает с
реальной только при
![]() (см. рисунок), в остальных случаях различие
существенное, поэтому следует пользоваться
ее математическим выражением.
(см. рисунок), в остальных случаях различие
существенное, поэтому следует пользоваться
ее математическим выражением.
Определение параметров колебательного звена.
Иногда форма записи ПФ колебательного звена может отличаться от стандартных. Возникает вопрос определения параметров Т и колебательного звена.
Например, ПФ двигателя постоянного тока по управляющему воздействию имеет вид:
![]() .
.
Здесь
![]() и
и
![]() .
Отсюда
.
Отсюда
![]()
![]() .
.
Если оказывается,
что
![]() ,
имеем колебательное звено. В противном
случае (
,
имеем колебательное звено. В противном
случае (![]() )
корни знаменателя ПФ становятся
действительными, тогда звено представляет
собой последовательное соединение двух
апериодических звеньев.
)
корни знаменателя ПФ становятся
действительными, тогда звено представляет
собой последовательное соединение двух
апериодических звеньев.
Таким образом,
значение
![]() говорит о том, какой характер переходного
процесса будет иметь место на выходе
звена. Применительно к двигателю
постоянного тока
говорит о том, какой характер переходного
процесса будет иметь место на выходе
звена. Применительно к двигателю
постоянного тока
![]() ,
когда
,
когда
![]() ,
и будет иметь место колебательный (с
перерегулированием) процесс при
скачкообразном приложении управляющего
воздействия. В противном случае
,
и будет иметь место колебательный (с
перерегулированием) процесс при
скачкообразном приложении управляющего
воздействия. В противном случае
![]() переходный процесс будет апериодическим
(с дотягиванием).
переходный процесс будет апериодическим
(с дотягиванием).
Форсирующее звено 2-го порядка
![]()
![]() – постоянная времени
– постоянная времени
![]()
![]()
Имеет ПФ, обратную ПФ колебательного
звена при
![]() ,
,
![]() .
Поэтому здесь вкратце приведем основные
математические зависимости.
.
Поэтому здесь вкратце приведем основные
математические зависимости.
Дифференциальное уравнение:
![]() .
.
Частотная характеристика:
![]() .
.
АЧХ ![]() .
.
ФЧХ ![]() .
.
ЛАЧХ ![]() .
.
ЛФЧХ ![]() .
.
Звено чистого (транспортного) запаздывания
Некоторые ОУ могут обладать запаздыванием (например, трубопроводы, длинные линии, транспортеры). Запаздывание проявляется в том, что при изменении входного воздействия выходная переменная начинает изменяться не сразу, а спустя некоторый промежуток времени , называемый временем чистого или транспортного запаздывания.
![]() .
.
П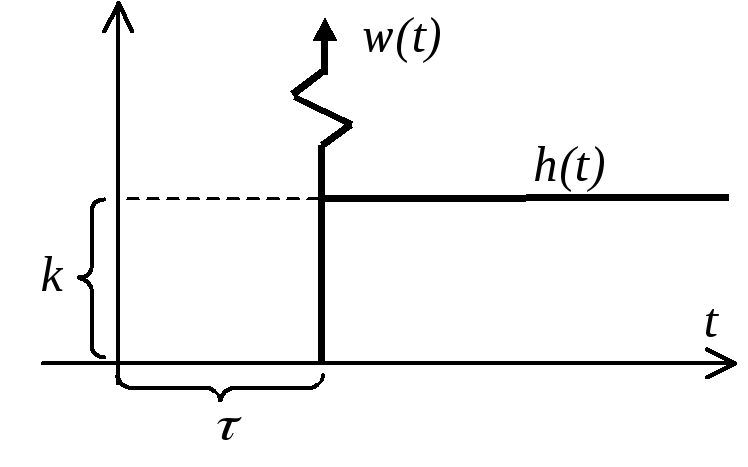 ереходная
функция (см. рисунок)
ереходная
функция (см. рисунок)
![]()
Весовая функция (см. рисунок)
![]()
Частотная характеристика:
![]()
АЧХ ![]() .
.
ФЧХ ![]() .
.
ЛАЧХ ![]() .
.
ЛФЧХ ![]() .
.
Построение логарифмических частотных характеристик
произвольной совокупности типовых звеньев
Пусть имеется произвольное последовательное соединение n типовых звеньев с результирующей ПФ
![]() (1)
(1)
По определению ЛАЧХ и ЛФЧХ вычисляются следующим образом:
![]() ;
;
![]() .
.
Таким образом, для построения ЛАЧХ или ЛФЧХ последовательного соединения звеньев следует построить соответствующие характеристики каждого звена, и затем геометрически их сложить.
Передаточную функцию (1) совокупности звеньев целесообразно представить в более развернутом виде:
![]() , (2)
, (2)
где
![]() – нормированная
ПФ – отношение
произведений ПФ элементарных звеньев
1-го и 2-го порядков (т.е., вида
– нормированная
ПФ – отношение
произведений ПФ элементарных звеньев
1-го и 2-го порядков (т.е., вида
![]() и
и
![]() при
при
![]() )
с единичным передаточным коэффициентом
(
)
с единичным передаточным коэффициентом
(![]() );
);
![]() – результирующий
коэффициент передачи (усиления);
– результирующий
коэффициент передачи (усиления);
![]() – порядок астатизма
ПФ (так наз. апериодической
нейтральности),
численно равный количеству последовательно
соединенных интеграторов в предположении,
что чистые дифференцирующие звенья
отсутствуют.
– порядок астатизма
ПФ (так наз. апериодической
нейтральности),
численно равный количеству последовательно
соединенных интеграторов в предположении,
что чистые дифференцирующие звенья
отсутствуют.
Пример. Построить асимптотические ЛАЧХ и ЛФЧХ звена с ПФ
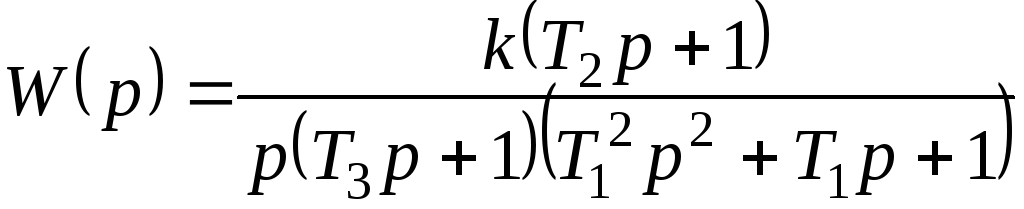 ,
,
где значение коэффициента усиления и
постоянных времени известны, и известно,
что
![]() .
.
Если рассматривать эту ПФ в виде (2), то
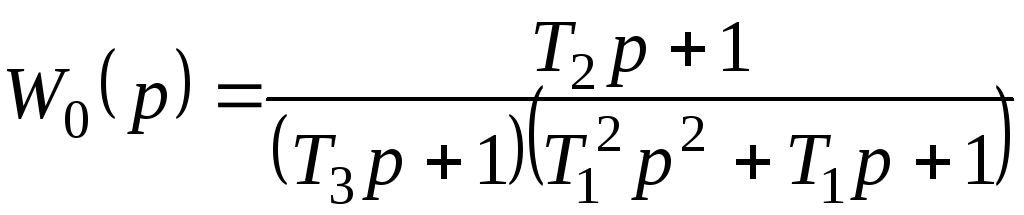 ;
; ![]() ;
; ![]() .
.
Очевидно, имеем последовательное
соединение четырех типовых звеньев:
интегратор с ПФ
![]() ;
форсирующее звено 1-го порядка с ПФ
;
форсирующее звено 1-го порядка с ПФ
![]() ;
апериодическое звено с ПФ
;
апериодическое звено с ПФ
![]() ;
колебательное звено с ПФ
;
колебательное звено с ПФ
![]() (
(![]() ).
).
Строим асимптотические ЛАЧХ каждого из звеньев (пунктирные линии) и их геометрическую сумму (сплошная линия), которая и является результирующей ЛАЧХ. Аналогично поступаем с ЛФЧХ.
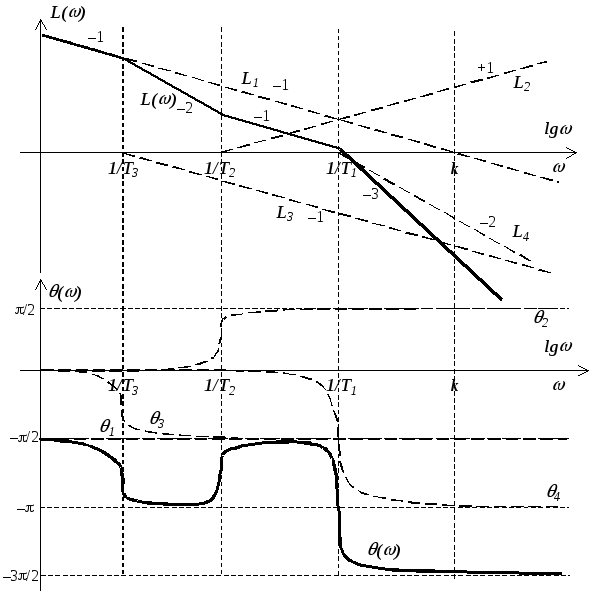
После анализа ЛАЧХ можно предложить следующее правило:
1) Пользуясь
представлением (2) передаточной функции,
вычисляют все частоты сопряжения
![]() (i
= 1, 2, …), которые нумеруют в порядке
возрастания и откладывают на оси частот;
(i
= 1, 2, …), которые нумеруют в порядке
возрастания и откладывают на оси частот;
2) Предварительную
ЛАЧХ начинают строить от области низких
частот, проводя прямую под наклоном
–![]() 20
дБ/дек (
20
дБ/дек (![]() )
так, чтобы она (или ее продолжение)
пересекала ось частот при частоте
)
так, чтобы она (или ее продолжение)
пересекала ось частот при частоте
![]() .
(Эта ЛАЧХ будет пересекать ось ординат
в точке
.
(Эта ЛАЧХ будет пересекать ось ординат
в точке
![]() .)
.)
Именно такой вид будет иметь ЛАЧХ
совокупности
![]() последовательно соединенных интеграторов,
соответствующая первому множителю ПФ
вида (2).
последовательно соединенных интеграторов,
соответствующая первому множителю ПФ
вида (2).
3) Низкочастотная
ЛАЧХ будет претерпевать изломы только
при частотах сопряжения
![]() ,
причем наклон будет изменяться на 20
дБ/дек (+1), если
,
причем наклон будет изменяться на 20
дБ/дек (+1), если
![]() -м
звеном оказывается форсирующее звено
1-го порядка, на –20 дБ/дек (–1) – если
апериодическое звено, на +40 дБ/дек (+2) –
если форсирующее звено 2-го порядка, на
–40 дБ/дек (–2) – если колебательное
звено.
-м
звеном оказывается форсирующее звено
1-го порядка, на –20 дБ/дек (–1) – если
апериодическое звено, на +40 дБ/дек (+2) –
если форсирующее звено 2-го порядка, на
–40 дБ/дек (–2) – если колебательное
звено.
Что касается ЛФЧХ, то следует построить ЛФЧХ отдельных звеньев, и затем геометрически их просуммировать.
Примечание. В случае наличия последовательно соединенного звена чистого запаздывания ЛАЧХ соединения остается без изменения, однако это звено окажет влияние на фазовый сдвиг.
Пример. Пользуясь правилом, построить ЛАЧХ соединения звеньев с ПФ:
![]()
Очевидно, что здесь
![]() ,
,
![]() ,
,
![]() .
.
Тогда
![]() ,
,
![]() .
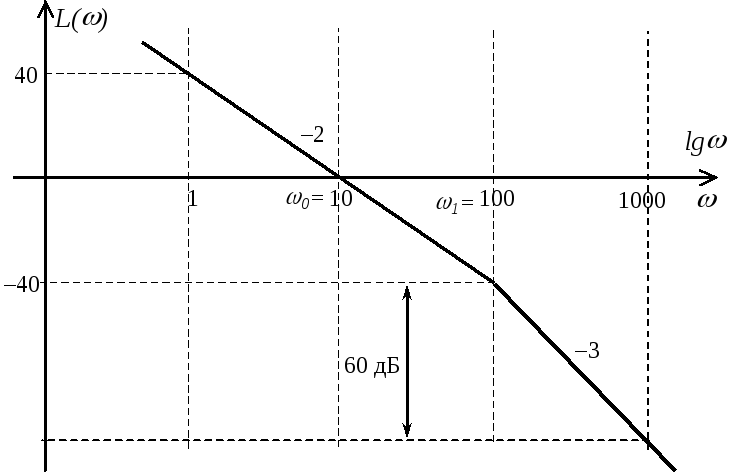
Проводим прямую под наклоном –2 (–40
дБ/дек), которая будет пересекать ось
частот в точке
.
Проводим прямую под наклоном –2 (–40
дБ/дек), которая будет пересекать ось
частот в точке
![]() .
При
.
При
![]() ЛАЧХ изменит наклон на –1, поскольку
ЛАЧХ изменит наклон на –1, поскольку
![]() соответствует частоте сопряжения
апериодического звена. Следовательно,
при
соответствует частоте сопряжения
апериодического звена. Следовательно,
при
![]() ЛАЧХ будет иметь наклон –3 (–2–1=–3).
ЛАЧХ будет иметь наклон –3 (–2–1=–3).
Лекция 6
(4 часа)
