Дифференциальные уравнения линейных сар

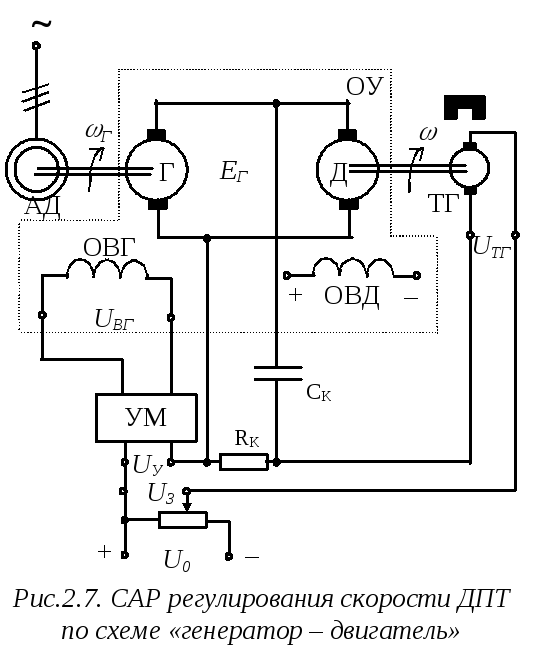
Рассмотрим САР частоты вращения двигателя постоянного тока независимого возбуждения, который питается от генератора независимого возбуждения (рис.2.7) (система «генератор – двигатель»).

Данная система, хотя еще и встречается на практике, в настоящее время является морально устаревшей. Выбор ее в данном вопросе удобен в том плане, что на ее примере можно наиболее наглядно получить типовые дифференциальные уравнения, используемые при анализе систем электропривода.

Объект управления САР содержит генератор (Г), вал которого вращается с помощью приводного АД, с обмоткой возбуждения ОВГ, и двигатель (Д) с обмоткой возбуждения ОВД. Величина ЭДС генератора E_Г регулируется за счет изменения напряжения U_ВГ на ОВГ, которое, в свою очередь формируется с помощью усилителя мощности (УМ), выполняющего роль преобразующего устройства. В качестве датчика регулируемой переменной (скорости двигателя) выступает тахогенератор постоянного тока (ТГ). Сигнал задания U_З формируется с помощью потенциометра, и, согласно электрической цепи, выполняющей функцию узла сравнения, оказывается равным сумме напряжения U_ТГ с выхода ТГ, напряжения U_K корректирующей цепи (R_K – C_K) и напряжения U_У на входе УМ. Корректирующая цепь необходима для придания САР требуемых динамических свойств.

Для математического описания САР выделяют ее отдельные элементы, которые обладают однонаправленными свойствами: выходной сигнал формируется в зависимости от входного, и не влияет на него. Согласно с таким принципом однонаправленности, в САР рис.2.7 можно выделить следующие элементы:

1. Генератор (Г). В качестве входа рассматриваем напряжение возбуждения U_ВГ, в качестве выхода – ЭДС генератора Е_Г. Условно записываем:

U_ВГ ® Е_Г (вход ® выход)

Обратное направление выбрать нельзя, поскольку Е_Г не влияет на U_ВГ, а лишь на частоту вращения w_Г. Кроме того, это противоречит функциональному назначению генератора.

2. Двигатель (Д):

Е_Г ® w

3. Тахогенератор (ТГ):

w ® U_ТГ

4. Усилитель мощности (УМ) считаем идеальным (внутреннее сопротивление равно нулю):

U_У ® U_ВГ

5. Узел сравнения (электрическая цепь) (УС):

U_У = U_З – U_ТГ – U_K

6. Корректирующая цепь (КЦ):

Е_Г ® U_K

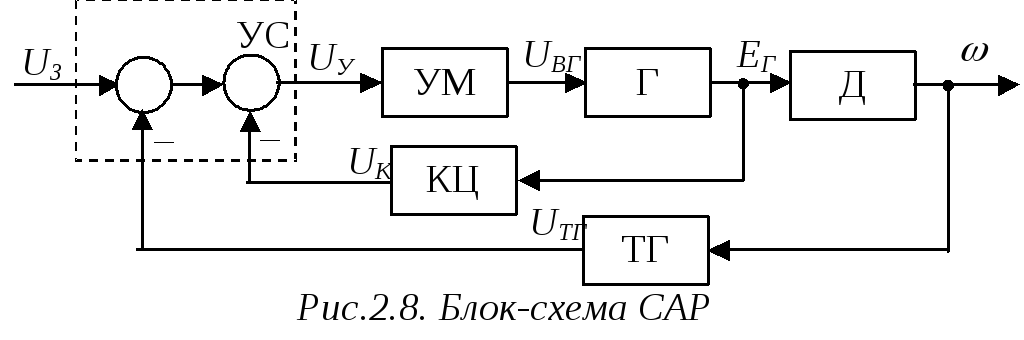
После такой детализации можно изобразить блок-схему рассматриваемой САР (рис.2.8).

Отметим здесь, что рассматриваемая САР является непрерывной.

Рассмотрим теперь более детально каждый блок для того, чтобы составить его математическое описание.

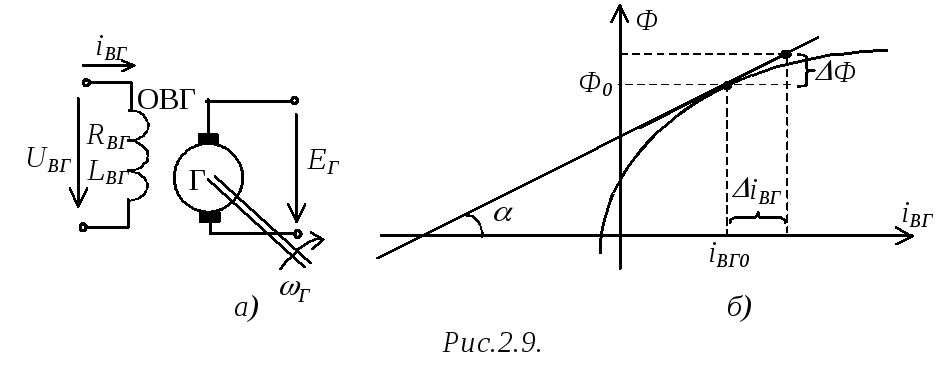
Генератор

Будем считать, что все полюса генератора соединены последовательно. Уравнение электрического равновесия (рис.2.9а) имеет вид:

,

где – число пар полюсов генератора; W_ВГ – число витков на полюс.

Цепь намагничивания генератора является нелинейной, поскольку (рис.2.9б). Для упрощения подвергнем ее линеаризации в окрестности рабочей точки с координатами , используя соображения, рассмотренные выше. После разложения функции в ряд Тейлора и пренебрежения малыми членами можно получить:

.

Приравнивая приращения и опуская символ , получим окончательное линеаризованное уравнение:

,

где .

После линеаризации уравнение электрического равновесия ОВГ можно записать в виде:

.

ЭДС генератора при неизменной частоте вращения вала w_Г пропорциональна магнитному потоку:

,

где – конструктивная постоянная генератора.

Выразим из последнего уравнения магнитный поток

и подставим в уравнение электрического равновесия:

,

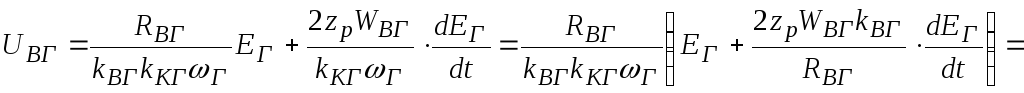
где – индуктивность возбуждения генератора.

Обозначим:

– коэффициент усиления генератора;

– постоянная времени генератора, с.

Теперь ДУ генератора можно записать в окончательном виде:

, (1)

где – оператор дифференцирования.

Это уравнение характеризует работу генератора как в статике, так и в динамике.

Двигатель

Двигатель постоянного тока с независимым постоянным возбуждением может быть описан следующими уравнениями:

Уравнение электрического равновесия цепи якоря:

,

где , – суммарные активное сопротивление и индуктивность цепи обмотки якоря двигателя, представляющие собой суммы соответствующих параметров генератора и двигателя, – противо-ЭДС двигателя; ; – конструктивная постоянная двигателя; – магнитный поток двигателя.

Уравнение электромагнитного момента:

.

Уравнение механической части (уравнение движения):

.

Будем считать пока, что нагрузка на валу двигателя отсутствует (). Уравнение момента подставим в уравнение движения, после чего выразим ток:

.

Выражение для тока подставим в уравнение электрического равновесия:

.

Разделив это уравнение на , получим ДУ двигателя в окончательном виде:

, (2)

где – электромагнитная постоянная времени цепи якоря, с;

– электромеханическая постоянная времени привода, с.

Тахогенератор

Если пренебречь оборотными пульсациями и внутренним сопротивлением тахогенератора, то напряжение на его выходе (равное наводимой ЭДС):

, (3)

где – коэффициент передачи тахогенератора, В*с.

Усилитель мощности

Пренебрегая внутренним сопротивлением усилителя мощности, для напряжения возбуждения генератора запишем уравнение:

, (4)

где – коэффициент передачи усилителя мощности.

Узел сравнения

Составленное ранее уравнение оставляем без изменения:

. (5)

Цепь корректирования

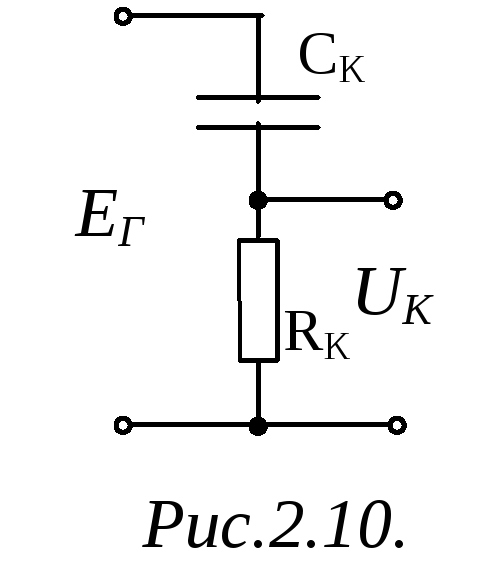ДУ для цепи корректирования (рис.2.10) имеет вид:

или

, (6)

где – постоянная времени цепи, с.

Очевидно, цепь корректирования работает только в переходных режимах. В установившихся режимах, когда , правая часть (6) равна нулю.