
- •2.1.1. Основные понятия
- •Виды матриц
- •2.1.2. Операции над матрицами
- •Умножение матрицы на число
- •Сложение и вычитание матриц
- •Умножение матриц
- •Транспонирование матриц
- •2.1.3. Матричная запись систем линейных уравнений.
- •2.1.4. Определители
- •Свойства определителей:
- •2.1.5. Решение систем линейных уравнений различными методами
- •Решение систем линейных уравнений методом Крамера
- •Решение систем линейных уравнений с использованием обратной матрицы.
- •Задания для самоподготовки
- •Образец выполнения задания
- •Задание № 1. Сложение матриц.
- •Задание № 2. Умножение матрицы на число
- •Задание № 3. Транспонирование матрицы
- •Задание № 4. Умножение матриц
- •Задание № 5. Вычисление определителя матрицы
- •Задание № 6. Вычисление обратной матрицы
- •Задание № 7. Решение систем линейных алгебраических уравнений
- •Индивидуальные задания для практической работы
- •3.1.1. Окружность
- •3.1.2. Эллипс
- •3.1.3. Гипербола
- •3.1.4. Парабола
- •Задания для самоподготовки
- •3.3. Образец выполнения задания
- •Задание № 1. Выбор диапазона данных и построение таблицы значений.
- •3.4. Индивидуальные задания для практической работы
- •Основные понятия
- •Цилиндрические поверхности
- •Свойства поверхностей второго порядка
- •Канонические уравнения поверхностей второго порядка
- •4.2. Задания для самоподготовки
- •4.3. Образец выполнения задания
- •4.4. Индивидуальные задания для практической работы
- •Литература
- •Учебное издание
- •400005, Г. Волгоград, пр.Ленина, 78.
-
Задание № 5. Вычисление определителя матрицы
Для вычисления определителя матрицы сформируем лист электронной таблицы:
-
Задать исходную матрицу. В нашем случае в качестве исходной матрицы рассмотрим матрицу С пятого порядка.
-
Определить место под результат.
-
Нажать пиктограмму
 в строке меню, в окне «Мастер функций»
найти функцию МОПРЕД
(см. рис. 15),
нажать
в строке меню, в окне «Мастер функций»
найти функцию МОПРЕД
(см. рис. 15),
нажать

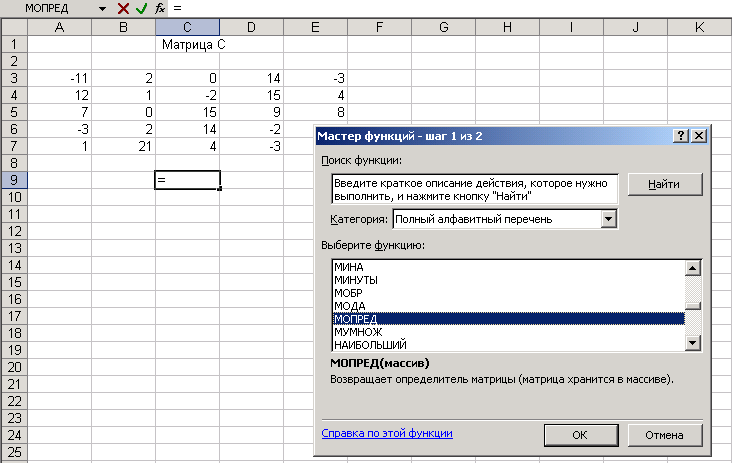
рис. 15.
-
Выполнить постановку задачи (рис.16.), задав в окне «Массив» диапазон адресов ячеек массива (матрицы).

рис.16.
-
Нажав
 ,
получить значение определителя (рис.17):
,
получить значение определителя (рис.17):

рис. 17.
-
Задание № 6. Вычисление обратной матрицы
Для вычисления определителя матрицы сформируем лист электронной таблицы:
-
Задать исходную матрицу. В нашем случае в качестве исходной матрицы рассмотрим матрицу С пятого порядка.
-
Определить место под результат.
-
Нажать пиктограмму
 в строке меню, в окне «Мастер функций»
найти функцию МОБР
и
нажать
в строке меню, в окне «Мастер функций»
найти функцию МОБР
и
нажать

-
Выполнить постановку задачи (рис.18.), задав в окне «Массив» диапазон адресов ячеек массива (матрицы).

рис. 18.
-
Для получения результата нажать одновременно клавиши Shift/Ctrl/Enter (рис.19).

рис.19.
-
Задание № 7. Решение систем линейных алгебраических уравнений
Решение систем линейных алгебраических уравнений всегда занимало математиков и для их решения было разработано немало численных методов, подразделяющихся на прямые и итерационные.
В EXCEL задача получения решения СЛУ решается с помощью вышеописанных матричных функций, для чего исходную систему надо представить в виде матричного уравнения.
Рассмотрим последовательность действий для получения решения СЛАУ на конкретном примере.

Для того, чтобы система имела решение необходимо и достаточно, чтобы определитель матрицы системы не был равен нулю.
Рассчитаем определитель системы, пользуясь функцией МОПРЕД (рис.18). Рассчитанное значение определителя системы равно 152 (см. рис. 20). Оно не равно нулю и, следовательно, можно продолжать процесс поиска решения.
Из
линейной алгебры известна матричная
запись системы уравнений и матричное
представление решения. Перепишем систему
в виде
![]() ,
где
,
где
 .
.
Используя функции EXCEL, получим:

рис. 20.
-
Индивидуальные задания для практической работы
-
Выполнить действия над матрицами.
-
Решить систему по формулам Крамера.
-
Решить систему с помощью обратной матрицы.
Вариант № 1.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 2.
1)
![]() ,
где
,
где
 и
и
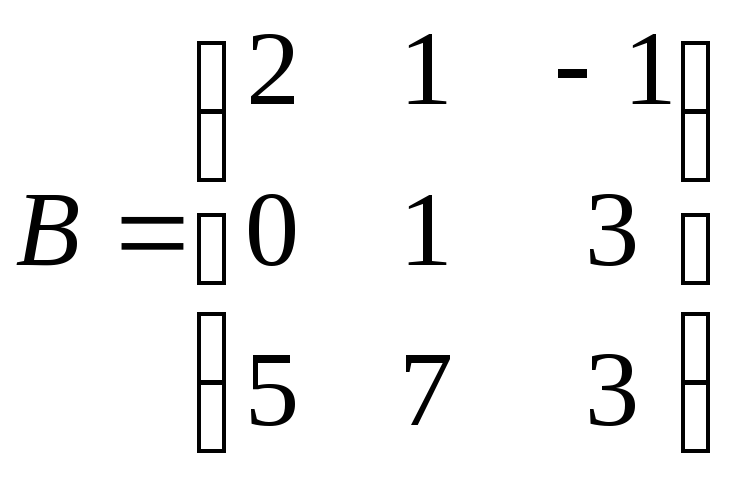 .
.
2)
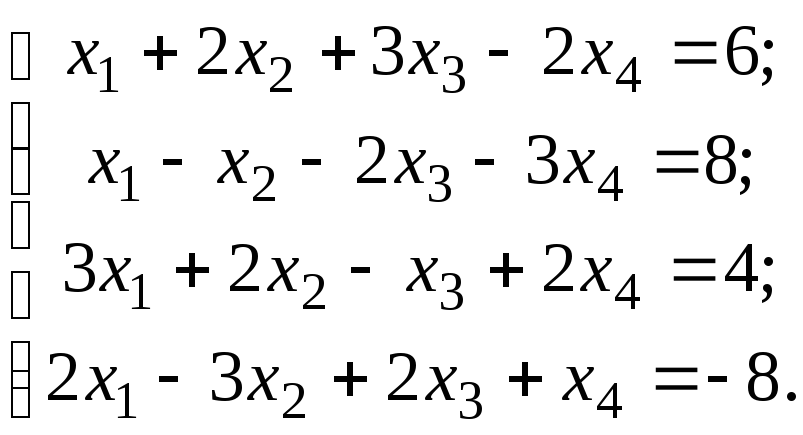 3)
3)

Вариант № 3.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 4.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 5.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 6.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
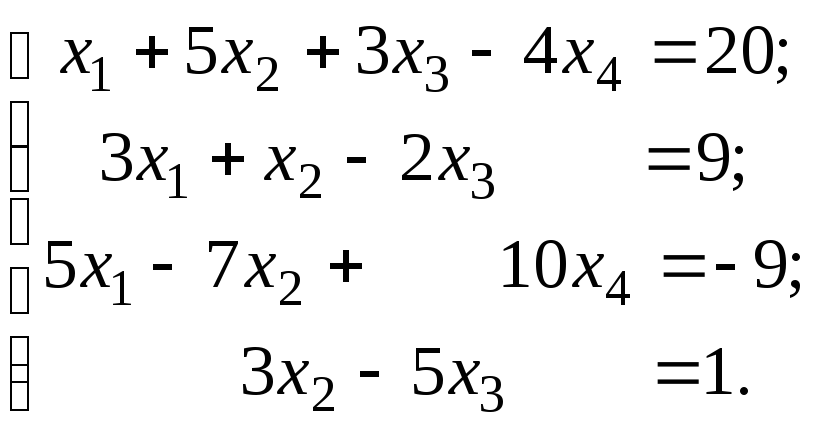 3)
3)

Вариант № 7.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 8.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 9.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 10.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 11.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
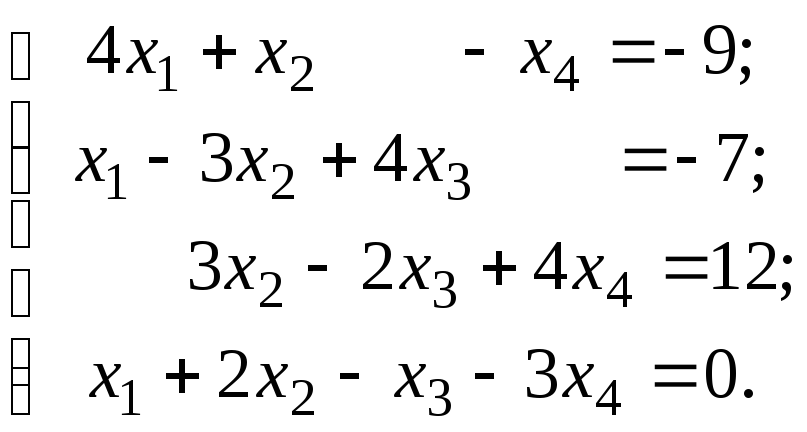 3)
3)

Вариант № 12.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 13.
1)
![]() ,
где
,
где
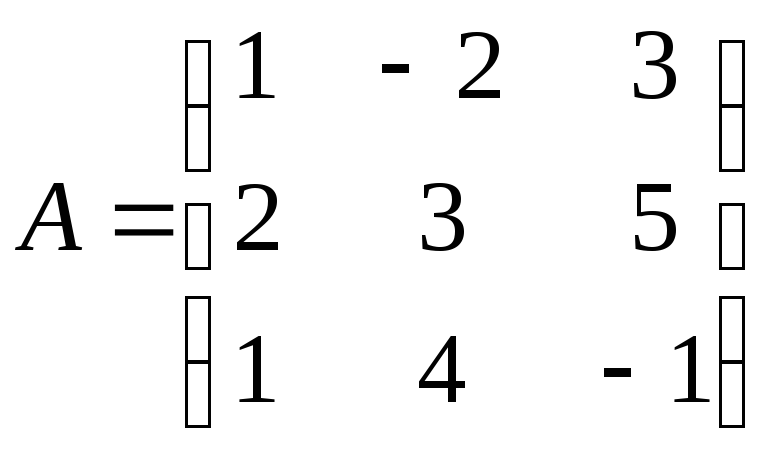 и
и
 .
.
2)
 3)
3)

Вариант № 14.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 15.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 16.
1)
![]() ,
где
,
где
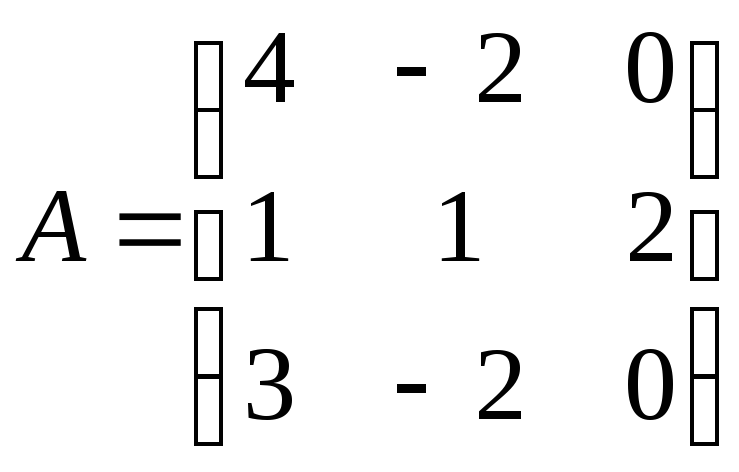 и
и
 .
.
2)
 3)
3)

Вариант № 17.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 18.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 19.
1)
![]() ,
где
,
где
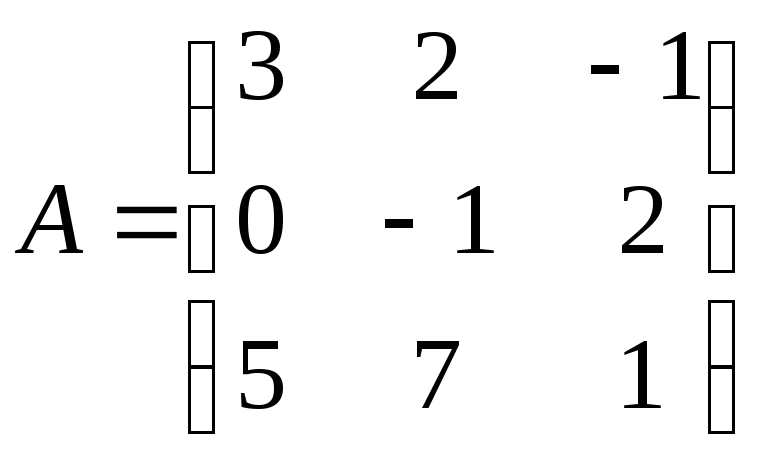 и
и
 .
.
2)
 3)
3)

Вариант № 20.
1)![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 21.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 22.
1)
![]() ,
где
,
где
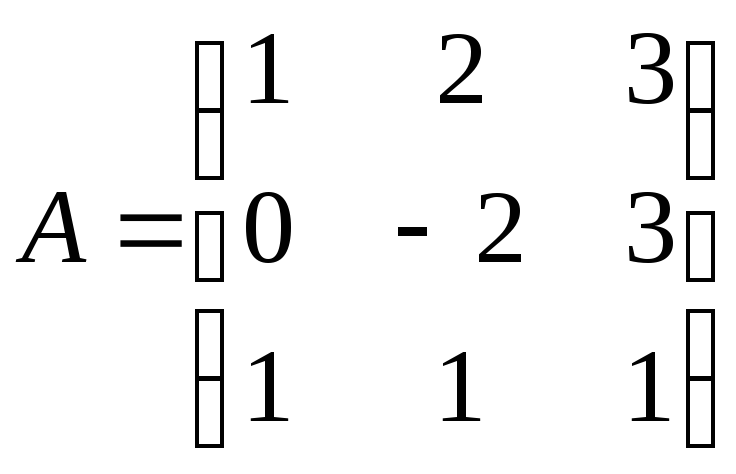 и
и
 .
.
2)
 3)
3)

Вариант № 23.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 24.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 25.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 26.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 27.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 28.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 29.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

Вариант № 30.
1)
![]() ,
где
,
где
 и
и
 .
.
2)
 3)
3)

3. Практическая работа 2.
«Построение точечных диаграмм»
(на примере построения кривых второго порядка).
3.1. Теоретическая часть
