
- •Львівський національний університет імені Івана Франка Економічний факультет
- •Доповідь №2
- •«Шляхи зниження ентропії в задачах планування»
- •Різноманітність та ентропія.
- •Закон необхідного різноманіття станів
- •Закон необхідного різноманіття в задачі планування випуску продукції
- •Шляхи зниження ентропії в задачах планування.
Міністерство освіти і науки, молоді та спорту України
Львівський національний університет імені Івана Франка Економічний факультет
Кафедра
економічної кібернетики
Доповідь №2
з курсу "Моделювання системних характеристик в економіці" на тему:
«Шляхи зниження ентропії в задачах планування»
Виконали:
Дух Володимир Ігорович
Роман Володимир Ігорович
Львів - 2011
Зміст:
-
Різноманітність та ентропія
-
Закон необхідного різноманіття станів
-
Закон необхідного різноманіття в задачі планування випуску продукції
-
Шляхи зниження ентропії в задачах планування.
-
Різноманітність та ентропія.
Будь-якій
системі
 властива деяка ступінь різноманітності,
яка за У. Р. Ешбі визначається множиною
можливостей її перебування в різних
станах. Цю ступінь різноманіття можна
охарактеризувати, задаючи таблицю
ймовірностей перебування системи в
кожному з можливих станів.
властива деяка ступінь різноманітності,
яка за У. Р. Ешбі визначається множиною
можливостей її перебування в різних
станах. Цю ступінь різноманіття можна
охарактеризувати, задаючи таблицю
ймовірностей перебування системи в
кожному з можливих станів.

де
 - можливий стан системи,
- можливий стан системи,
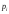 - ймовірність того, що система перебуває
в цьому стані.
- ймовірність того, що система перебуває
в цьому стані.
Стан
системи
 можна представити одним чи декількома
параметрами, не всі з яких мають кількісне
вираження. Важливим моментом є те, що
всі
можна представити одним чи декількома
параметрами, не всі з яких мають кількісне
вираження. Важливим моментом є те, що
всі
 можливих станів різні і вони визначають
ступінь різноманітності системи.
можливих станів різні і вони визначають
ступінь різноманітності системи.
В якості міри різноманітності для множини можливих станів системи використовується поняття ентропії.
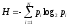
Ця
величина представляє собою математичне
сподівання логарифму ймовірності
перебування системи
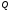 в стані
в стані
 ,
і відповідає введеній Шенноном в теорії
інформації «мірі невизначеності».
,
і відповідає введеній Шенноном в теорії
інформації «мірі невизначеності».
Таким
чином, невизначеність виконання одного
з можливих станів системи залежить як
від числа можливих станів, так і від
розподілу ймовірностей цих станів.
Наприклад, якщо виконання будь-якого з
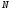 варіантів рівноймовірно, то невизначеність
вибору максимальна і визначається
загальною кількістю варіантів.
варіантів рівноймовірно, то невизначеність
вибору максимальна і визначається
загальною кількістю варіантів.
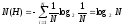
Тобто змістом поняття ентропія є міра різноманіття можливих станів системи.
Розглядаючи план як систему, можна сказати, що йому також притаманна властивість ентропії, оскільки реалізація прийнятого рішення в силу суттєвої невизначеності майбутньої поведінки планованої системи не може бути однозначною.
Очевидно, що з точки зору прийнятого управлінського рішення можливе різноманіття необхідно обмежувати. Ступінь обмеження і визначає можливість прийняття визначеного, і зокрема оптимального, рішення при управлінні.
Під обмеженням різноманітності розуміється його зменшення в порівнянні з абстрактно можливим внаслідок яких-небудь умов, які накладаються на систему, чи внутрішніх її характеристик. В якості міри обмеження різноманіття може бути використана широко використовуване в теорії інформації поняття надлишковості:
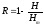
де
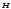 - ентропія системи в умовах заданих
обмежень різноманіття;
- ентропія системи в умовах заданих
обмежень різноманіття;
 -
максимальна ентропія системи в умовах
найбільшого для даної системи ступеня
незалежності станів.
-
максимальна ентропія системи в умовах
найбільшого для даної системи ступеня
незалежності станів.
Найбільша
степінь обмеження різноманіття відповідає
реалізації єдиного можливого стану.
При цьому
 , тобто множина не виявляє ніякого
різноманіття, а надлишковість максимальна
і рівна одиниці. Загалом ентропія
будь-якої достовірної події (чи прийнятої
як достовірної) рівна нулеві, оскільки
, тобто множина не виявляє ніякого
різноманіття, а надлишковість максимальна
і рівна одиниці. Загалом ентропія
будь-якої достовірної події (чи прийнятої
як достовірної) рівна нулеві, оскільки
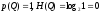 .
.
Навпаки,
якщо є тільки одне обмеження загальної
кількості різноманітних можливостей
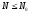 і всі можливі стани рівноймовірні, то
ентропія досягає максимального значення
при цих обмеженнях:
і всі можливі стани рівноймовірні, то
ентропія досягає максимального значення
при цих обмеженнях:
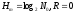 .
.
Розглянемо спочатку, з яких позицій доцільно використовувати поняття ентропії для розв’язування задач, пов’язаних з перспективним плануванням.
В цьому аспекті ентропія є властивістю,принципово властивим фізичній, а не економічній системі, і навіть глибока аналогія моделей не дозволяє вести про неї мову як про властивість, яка характеризує безпосередньо планову систему.
Продуктивним є інший аспект використання поняття ентропії в економіці – це використання шенноновського поняття ентропії безпосередньо як кількісної міри економічної інформації:
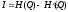
де
 - кількість інформації, яка міститься
в одному повідомленні;
- кількість інформації, яка міститься
в одному повідомленні;
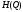 -
ентропія системи
-
ентропія системи
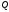 до отримання повідомлення (апріорна
ентропія);
до отримання повідомлення (апріорна
ентропія);
 -
ентропія системи
-
ентропія системи
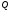 після отримання повідомлення (апостеріорна
ентропія).
після отримання повідомлення (апостеріорна
ентропія).
Використання такого підходу досить продуктивно при створенні автоматизованих систем управління виробництвом. Однак цей напрямок відноситься лише до питань збору, передачі та обробки інформації в економічній системі, а не до характеристик плану як складної системи, хоча формально поняття ентропії як кількісної міри інформації і як міри різноманіття станів системи ідентичні і визначаються відношенням
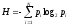 .
.
Якщо орієнтуватися на зміст поняття ентропія, як він визначається в теорії систем, то і тут можливі різні використання даного поняття. Зупинимося детальніше на їх змісті і можливостях використання для характеристик плану як складної системи.
Будемо використовувати дві модифікації поняття внутрішньоструктурної ентропії:
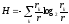
 ,-
,-
обидва ці поняття відображають внутрішню структуру плану.
Ентропія
станів визначається як міра різноманіття
множини можливих варіантів плану
 .
Інакше кажучи, якщо необхідно зробити
вибір серед сукупності планів
.
Інакше кажучи, якщо необхідно зробити
вибір серед сукупності планів
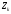 ,
яким відповідають ймовірності
,
яким відповідають ймовірності
 ,
то різноманіття цього вибору визначається
відповідною ентропією:
,
то різноманіття цього вибору визначається
відповідною ентропією:
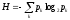 .
.
В такому аспекті ентропія по своєму змісту відповідає аналогічному поняттю теорії систем.
Нехай задача планування формулюється як задача лінійного програмування:

Умови, які визначають множину можливих планів
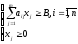
Виділяють в усьому просторі станів системи випуклий багатогранник. Можна вважати, що всі стани системи в ньому рівноймовірні. В такому випадку:
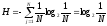
де
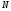 - кількість різноманітних станів системи.
- кількість різноманітних станів системи.
Оскільки множина допустимих планів в даному випадку нескінченна, тоді умови:
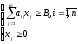
слабо
обмежують різноманітність
 .
.
Як відомо, розв’язок задач оптимізації виду:
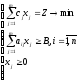
знаходиться серед так званих опорних планів, які відповідають кутовим точкам багатогранника рішень. Тому можна ввести додаткову умову – «виділити опорні плани». Таке обмеження різноманіття перетворює безкінечну множину можливих станів в скінченне, яке залежить від рангів матриці обмежень і розширеної матриці. Міра ентропії в такому випадку у відповідності з
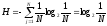
стає хоча б скінченним числом.
Наступна умова, яка приводить до зниження ентропії, може відображати той факт, що серед множини опорних планів потрібно розглядати лише ті, в базис яких входить обов’язково визначений перелік об’єктів (як, наприклад, в транспортній задачі з виключенням перевезень). Ентропія в такому випадку знижується навіть при рівноймовірній реалізації станів, оскільки потужність множини можливих станів нижча.
І, наостанок, суттєво обмежує різноманіття, зводячи його практично до нуля, додавання до обмежень
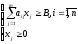
цільової функції в умовах єдиного розв’язку системи.
Зауваження. Ентропія станів завжди рівна нулю, якщо розглядається один стан системи, якою б вона складною не була.
Таким чином, ентропія плану як системи є її невід’ємною властивістю, важливою для системного аналізу плану.
