
- •Предмет физики
- •Структура физического познания.
- •Пространственно-временная область изучаемых физикой объектов
- •Физические теории
- •Раздел 1. Физические основы механики.
- •Глава 1. Кинематика.
- •§1.1. Система отсчета. Инерциальные системы отсчета. Принцип относительности.
- •§1.2. Кинематика материальной точки.
- •§1.3. Равномерное и равнопеременное движения.
- •§ 1.4. Кинематика вращательного движения.
- •§ 1.5. Краткие итоги главы 1.
- •Глава 2. Динамика материальной точки.
- •§ 2.1 .Задача динамики. Состояние материальной точки. Динамические характеристики движения.
- •§ 2.2. Законы Ньютона. Второй закон как уравнение движения.
- •§ 2.3. Силы в механике.
- •§ 2.4. Работа силы. Мощность.
- •§ 2.4. Механическая энергия.
- •§ 2.5. Краткие итоги главы 2
- •Глава 3.Законы сохранения в механике.
- •§ 3.1.Фундаментальный характер законов сохранения
- •§ 3.2. Закон сохранения импульса.
- •§ 3.3. Закон сохранения механической энергии
- •§ 3.4. Столкновения тел
- •Глава 4. Динамика вращательного движения.
- •§ 4.1. Кинетическая энергия вращающегося и катящегося тел
- •§ 4.2. Момент инерции
- •§ 4.3. Работа и мощность при вращательном движении. Момент силы относительно оси
- •§ 4.4. Уравнение динамики вращательного движения.
- •§ 4.5. Закон сохранения момента импульса
- •§ 4.6. Краткие итоги главы 4
- •Раздел 2. Молекулярная физика и термодинамика
- •Глава 5. Кинетическая теория
- •§ 5.1. Тепловое движение
- •§ 5.2. Основное уравнение кинетической теории газа
- •§ 5.3. Уравнение Клапейрона – Менделеева
- •§ 5.4. Молекулярно-кинетический смысл абсолютной температуры. Средняя энергия теплового движения молекулы
- •§ 5.5. Распределение Максвелла молекул газа по скоростям
- •§ 5.6. Барометрическая формула. Распределение Больцмана.
- •§ 5.7. Среднее число столкновений и средняя длина свободного пробега молекул.
- •§ 5.8. Выводы из главы 5.
- •Глава 6. Термодинамика.
- •§ 6.1. Тепловые процессы
- •§ 6.2. Первое начало термодинамики.
- •§ 6.3 Изопроцессы.
- •§ 6.4. Тепловая и холодильная машины
- •§ 6.5. Цикл Карно
- •§ 6.6. Энтропия.
- •§ 6.7. Второе начало термодинамики.
- •§ 6.8. Основные выводы главы 6.
- •Раздел 3. Электромагнетизм
- •Глава 7. Электростатика
- •§7.1.Электрический заряд. Закон Кулона.
- •§7.2. Электрическое поле. Напряженность.
- •§ 7.3. Теорема Гаусса.
- •§ 7.4. Потенциал и работа электростатического поля.
- •§ 7.5. Связь напряженности и потенциала электростатического поля.
- •§ 7.6.Электростатическое поле в веществе.
- •§ 7.7. Электроемкость. Конденсатор.
- •§ 7.8. Энергия электрического поля.
- •Глава 8. Постоянный электрический ток.
- •§ 8.1. Электрический ток: сила тока, плотность тока
- •§ 8.2. Механизм электропроводности
- •§ 8.3. Законы постоянного тока.
- •§ 8.4. Работа и мощность тока
- •Глава 9. Магнитное поле тока
- •§ 9.1 Магнитное взаимодействие. Магнитное поле
- •§ 9.2. Закон Био-Савара-Лапласа
- •9.3. Вихревой характер магнитного поля.
- •§ 9.4. Действие магнитного поля на токи и движущиеся электрические заряды
- •§ 9.5. Магнитное поле в веществе
- •Глава 10. Явление электромагнитной индукции
- •§ 10.1. Основной закон электромагнитной индукции
- •§ 10.2. Самоиндукция и взаимная индукция
- •§ 10.3. Энергия магнитного поля
- •§ 10.4. Вихревое электрическое поле. Уравнения Максвелла
§ 5.2. Основное уравнение кинетической теории газа
1. Атомы и молекулы вещества на небольших по сравнению с их размерами расстояниях притягиваются друг к другу, причем, силы притяжения быстро уменьшаются при увеличении расстояния. В газах его частицы большую часть времени находятся так далеко друг от друга, что силы притяжения не в состоянии противодействовать разбрасывающему их тепловому движению. При сближении частиц на расстояния, соответствующие столкновению, силы притяжения частиц сменяются силами отталкивания, и частицы вновь разлетаются. Можно считать, что между столкновениями частицы движутся свободно, при этом время свободного движения значительно превосходит время столкновений, и газ вследствие теплового движения всегда полностью занимает предоставленный ему объем. Отсюда модель идеального газа:
-
собственный объем молекул мал по сравнению с объемом газа (т.е.с объемом сосуда):
-
потенциальная энергия взаимодействия молекул пренебрежимо мала по сравнению с кинетической энергией хаотического движения, так что можно считать, что между двумя последовательными столкновениями частицы движутся свободно, т.е. равномерно и прямолинейно;
-
вследствие хаотичности любые направления движения частиц равновероятны, т.е. в любом направлении в любой момент времени движется примерно одинаковое число частиц;
-
соударения молекул друг с другом и со стенками сосуда упругие.
2. При столкновении со стенкой сосуда
молекула сообщает ей импульс. Напомним,
что переданный в единицу времени импульс
равен силе, действующей на стенку, а
сила, направленная перпендикулярно к
поверхности, и отнесенная к единице
площади поверхности, равна давлению:
 .
Для простоты рассмотрим сосуд
прямоугольной формы объемом V=Sl,
где S – площадь
боковой стенки, перпендикулярной оси
х, l - длина
ребра вдоль оси х (см. рис. 20). Одна
из молекул (ее масса m0)
летит вдоль оси х со скоростью υ
из точки 1, в точке 2 упруго сталкивается
со стенкой, сообщает ей импульс 2m0υ
и отскакивает без потери скорости к
противоположной стенке. Ударившись в
точке 1, молекула опять движется в точку
2 и, спустя время
.
Для простоты рассмотрим сосуд
прямоугольной формы объемом V=Sl,
где S – площадь
боковой стенки, перпендикулярной оси
х, l - длина
ребра вдоль оси х (см. рис. 20). Одна
из молекул (ее масса m0)
летит вдоль оси х со скоростью υ
из точки 1, в точке 2 упруго сталкивается
со стенкой, сообщает ей импульс 2m0υ
и отскакивает без потери скорости к
противоположной стенке. Ударившись в
точке 1, молекула опять движется в точку
2 и, спустя время
 опять
сообщит стенке такой же импульс. За
единицу времени этот процесс произойдет
1/ раз, так что
удары одной молекулы о стенку сосуда
создадут силу m0υ
2/l.
опять
сообщит стенке такой же импульс. За
единицу времени этот процесс произойдет
1/ раз, так что
удары одной молекулы о стенку сосуда
создадут силу m0υ
2/l. 
Учитывая,
что в сосуде N
молекул, и их направления движения
равновероятны, без потери общности
рассуждений можем предположить, что
вдоль оси х движется 1/3 всех молекул,
и их общая сила давления на стенку равна
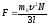 .
Давление
.
Давление
 ,
где
,
где

 - концентрация молекул, т.е. их число в
единице объема. Учтем, что скорости
движения молекул различны, и вклад
каждой молекулы в давление пропорционален
квадрату ее скорости, тогда
- концентрация молекул, т.е. их число в
единице объема. Учтем, что скорости
движения молекул различны, и вклад
каждой молекулы в давление пропорционален
квадрату ее скорости, тогда
 (5.2.1)
(5.2.1)
Здесь <
υ 2> - среднее значение
квадрата скорости, оно равно сумме
квадратов скоростей всех молекул,
деленной на их число. Эта величина также
называется квадратом средней квадратичной
скорости:
 .
Формула (5.2.1) выражает уравнение
молекулярно-кинетической теории
давления газа. Она показывает, что
давление газа – статистический параметр,
и равно среднему импульсу, переданному
единице площади стенки сосуда в единицу
времени при столкновении с ней молекул
вследствие их теплового движения.
Заметим, что газ, находящийся в состоянии
термодинамического равновесия, такое
давление будет оказывать на все стенки
сосуда любой формы.
.
Формула (5.2.1) выражает уравнение
молекулярно-кинетической теории
давления газа. Она показывает, что
давление газа – статистический параметр,
и равно среднему импульсу, переданному
единице площади стенки сосуда в единицу
времени при столкновении с ней молекул
вследствие их теплового движения.
Заметим, что газ, находящийся в состоянии
термодинамического равновесия, такое
давление будет оказывать на все стенки
сосуда любой формы.
3. В рассмотренной модели идеального
газа молекулы считаются материальными
точками. Кинетическая энергия теплового
движения
 у разных молекул разная вследствие
различия скоростей хаотического
движения. Усредним ее по всем молекулам.
и назовем средней кинетической
энергией поступательного хаотического
движения молекул <Eпост>.
Она выражается формулой:
у разных молекул разная вследствие
различия скоростей хаотического
движения. Усредним ее по всем молекулам.
и назовем средней кинетической
энергией поступательного хаотического
движения молекул <Eпост>.
Она выражается формулой:
<Eпост>= (5.2.2)
(5.2.2)
Основное уравнение кинетической теории газа можно записать еще и так:
 (5.2.3)
(5.2.3)
Уравнение (5.2.3) констатирует, что давление идеального газа зависит от концентрации молекул и их средней энергии поступательного движения. Формулы основного уравнения кинетической теории (5.2.1) и (5.2.3) связывают между собой величины, усредненные по всем молекулам: p, n, <Eпост>. Эти величины характеризуют не отдельную молекулу, а всю рассматриваемую термодинамическую систему – газ и являются характеристиками (параметрами) состояния газа. Таким образом, основное уравнение кинетической теории идеального газа является уравнением состояния идеального газа.
