§ 3.2. Закон сохранения импульса.

1. Совокупность тел, взаимодействующих только между собой, образует замкнутую систему тел. Взаимодействие между телами создает внутренние силы, внешние силы отсутствуют. Импульс системы n тел равен векторной сумме импульсов всех тел системы:

(3.2.1)

2. Пусть замкнутая система состоит из двух взаимодействующих тел. Импульс каждого тела вследствие взаимодействия изменяется согласно второму закону Ньютона: , . Учитывая, что силы взаимодействия подчиняются третьему закону Ньютона (), получаем: , т.е. . Полученный результат показывает, что импульс каждого тела в замкнутой системе вследствие взаимодействия может изменяться, но так, что их сумма остается неизменной. Этот результат легко обобщить не произвольное число тел замкнутой системы. Импульс замкнутой системы тел сохраняется – это формулировка закона сохранения импульса. В классической механике он имеет вид:

(3.2.2)

Напомним, что одному векторному уравнению в трехмерной декартовой системе координат соответствуют три скалярных. Если на систему тел действуют внешние силы, но в некотором направлении система замкнута и внешние силы отсутствуют, то в этом направлении сохраняется ее импульс. На практике немало тому примеров: отдача при стрельбе, реактивное движение и т.п.

3. В классической механике законы Ньютона и закон сохранения импульса выражают одни и те же свойства окружающего мира, однако, как мы обсуждали в предыдущем параграфе, закон сохранения импульса имеет более широкую область применения и выполняется для квантовых систем.

4. Импульс тела имеет вышедшее из употребления, но более точно отражающее его физический смысл название – количество движения, т.е. «запас движения». Закон сохранения импульса является законом сохранения «запаса движения». Действительно, из практики мы знаем, что перекладывание, например, денег из одного кармана в другой или раскладывание их по разным карманам не изменяет их сумму. Об этом же говорит арифметическое правило: от перемены мест слагаемых сумма не изменяется. Природа едина, и ее законы универсальны.

§ 3.3. Закон сохранения механической энергии

1. Пусть тело (м.т.) движется под действием консервативной силы. Ее работа превращается в приращение кинетической энергии тела (см. формулу 2.4.3): и происходит за счет уменьшения потенциальной энергии (см. формулу 2.4.4): 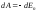. Отсюда следует: , т.е. полная механическая энергия тела сохраняется. Совокупность сил, действующих на тело в каждой точке пространства, образует поле сил. Поле консервативных сил называется потенциальным силовым полем. Закон сохранения энергии для тела в потенциальном силовом поле имеет вид:

Е=Е_к+Е_п=const (3.3.1)

Примеры действия этого закона на практике нам хорошо известны. Мячик, выпущенный из рук, падая под действием силы тяжести, ускоряется, и его потенциальная энергия превращается в кинетическую. Ударившись о пол, мячик отскакивает и, замедляясь, движется вверх – его кинетическая энергия переходит в потенциальную. Если бы не было неконсервативной силы сопротивления воздуха, то идеально упругий мячик поднялся бы на исходную высоту, а затем его падения и подскоки продолжались бы бесконечно долго.

2. Закон сохранения механической энергии можно обобщить на замкнутую систему тел, взаимодействующих между собой консервативными силами. При этом полная механическая энергия системы складывается из кинетических энергий отдельных тел и потенциальная энергия взаимодействия всех тел системы, зависящей от их взаимного расположения.

3. Если на систему тел действуют внешние силы, или внутри нее есть неконсервативные силы, то их работа изменяет механическую энергию. Например, работа силы трения всегда отрицательна, в результате механическая энергия уменьшается, расходуется на работу сил трения. В этом случае можно говорить о законе изменения механической энергии

Е=Е₂ –Е₁=А (3.3.2)

Он утверждает, что изменение механической энергии незамкнутой неконсервативной системы тел, равное разности ее конечного и начального значений, равно работе внешних и неконсервативных сил. Формула (3.3.2) имеет большое практическое значение. Рассмотрим, например, как скорость влияет на длину тормозного пути: Е = mv²/2, А=F_трS, так что при увеличении скорости в 2 раза тормозной путь увеличивается в 4 раза.

4. Помимо механической энергии существуют другие формы энергии, связанные с другими видами движения материи: тепловая, электрическая и т.д., которые могут превращаться друга в друга в эквивалентных количествах. С учетом разных форм энергии закон сохранения энергии приобретает всеобщий характер и превращается в один из наиболее общих законов физики: он утверждает количественную неизменность энергии замкнутой системы при качественном изменении формы энергии при изменении формы движения.