1.5. Методи побудови початкового базисного плану злп

З геометричної інтерпритації ЗЛП видно, що оптимальний план завжди досягається в одній із крайніх точок множини , а оскільки кількість крайніх точок кінцева, то логічно, що необхідно сконструювати алгоритми методів рішення ЗЛП, так, щоб впорядковано переходити від однієї крайньої точки до іншої.

Впорядкований перебір вершин (для ЗЛП на ) означає, що ми повинні перейти від однієї точки до іншої так, щоб значення цільової функції в результаті переходу збільшувалось.

Для того, щоб повністю дослідити ЗЛП необхідно:

1. або знайти значення ;

2. або показати, що лінійна форма ЗЛП необмежена на множині своїх планів;

3. або встановити несумісність умов ЗЛП, тобто показати, що область .

У всіх трьох випадках для дослідження ЗЛП необхідно починати перебір вершин області від однієї з них. Будемо називати цю вершину початковим базисним планом.

Таким чином, щоб побудувати початковий базисний план для ЗЛП необхідно:

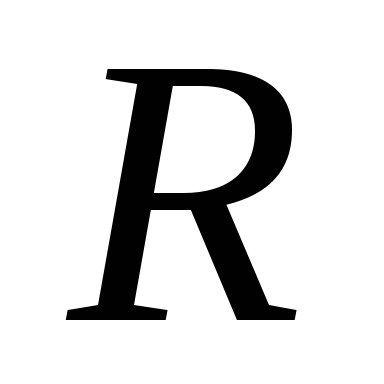1. Помножити на , ті умови із області , для яких ;

2. До умов типу „” додати доповнюючу змінну ;

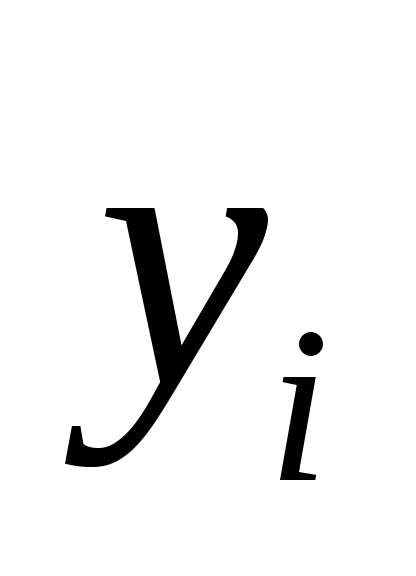3. До умов типу „=” додати штучну змінну ;

4. До умов типу „” додати .

Доповнюючі змінні входять в цільову функцію із коефіцієнтом 0, а штучні змінні із коефіцієнтами (), де – достатньо велике додатнє число для задачі на і достатньо велике від’ємне число для задачі на .

Приклад. Побудувати початковий базисний план для задачі лінійного програмування заданої у вигляді:

Побудуємо початковий базисний план для цієї задачі використовуючи описані підходи, отримаєм¹ задачу виду:

Таким чином початковий базисний план для отриманої в результаті перетворення задачі очевидний, а саме

1.6. Прямий симплексний метод розвязку злп

Найбільш широко відомим числовим методом рішення задач лінійного програмування є симплексний метод або метод послідовного покращення плану.

Для викладу симплексного методу припустимо, щоЗЛП представлена у вигляді:

(33)

Ввівши для задачі (33) позначення , , приведемо її до вигляду:

(34)

Відносно отриманої задачі (34) зробимо наступні припущення:

1. rang;

2. Задача (34) є невиродженою.

Невиродженою будемо називати ЗЛП для якої всі її базисні плани невироджені. Невиродженим базисним планом називається такий план, всі компоненти якого строго додатні.

Зрозуміло, що для невиродженої задачі . З геометричної точки зору умова невироженості означає, що в ЗЛП відсутні вершини, в яких перетиналось би більше ніж граничних гіперплощин (на площині прямих).

Запишемо матрицю умов задачі так ,

де:

- базисна підматриця (із векторів при базисних змінних);

- небазисна підматриця.

Відповідно , .

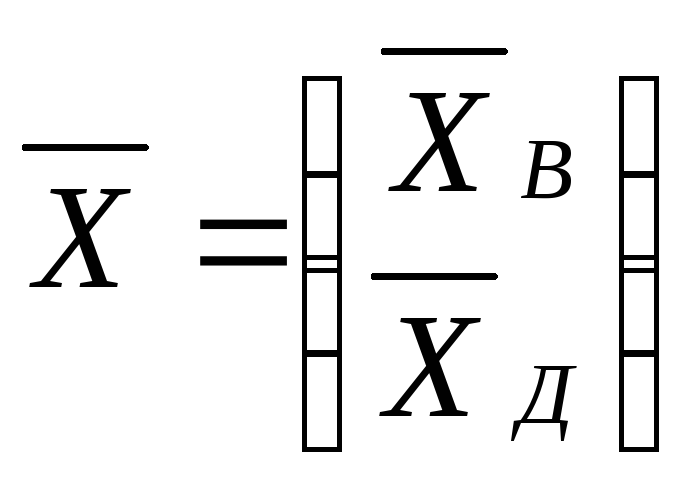Із області обмежень задачі (34) визначимо базисні змінні отримаємо

Помножимо останню рівність на матрицю обернену до базисної , оскільки задача, що розглядається невироджена, то існує.

Звідси:

(35)

Також очевидно із (35), що базисний план для задачі (34) запишеться:

(36)

Підставимо отримане значення в цільову функцію задачі (34) маємо:

(37)

Зрозуміло, що при початковому базисному плані (36) значення функції, яка оптимізується, буде рівним . Позначимо через величину , де:

- -тий стовбець матриці умов ;

- коефіцієнт при -тій змінній у цільовій функції.

Величини називають оцінками, а вектор - вектором оцінок.

Покажемо, що якщо – базисна змінна, тоді відповідне . Для визначення оцінки скористаємося формулою ,

Дійсно ( - вектор, у якого на місці стоїть 1, всі інші елементи рівні 0). Тоді .

Запишемо вектор у вигляді , де

- відповідає змінним (-мірний вектор);

- відповідає змінним (-мірний вектор).

тоді

(38)

(39)

Співвідношення (39) справедливе, оскільки у цільову функцію доповнюючі змінні входять із нульовими коефіцієнтами, а при змінних стоїть одинична матриця. Використавши вектор оцінок вираз (37) можна переписати у вигляді:

(40)

Відносно вектора оцінок можна виділити два випадки:

1. , , ;

2. , .

Покажемо, що у першому випадку знайдено оптимальний базисний план ЗЛП, тобто задача розв’язана, а у другому випадку або лінійна форма ЗЛП необмежена на множині своїх планів, або можна перейти до наступного базисного плану, який покращить значення цільової функції задачі, що розглядається.

У першому випадку цільову функцію збільшити неможливо за рахунок збільшення значення небазисних змінних, оскільки всі оцінки цих змінних додатні, а тому в (37) значення збільшити невдається.

Нехай серед компонент вектора , . Із виразу (40) видно, що в цьому випадку значення функції, що аналізується, можна збільшити на величину . Оскільки задача (34) на , то очевидно, що чим більше значення ми надамо величині , тим на більшу величину зросте значення досліджуваної цільової функції ЗЛП.

Однак можна збільшувати доти, поки одна із базисних змінних не перетвориться в , тобто найбільше значення, яке може мати змінна рівне числу

(41)

- вектор вільних членів в новому базисі;

- вектор коефіцієнтів при змінній в новому базисі.

Можуть виникнути два випадки:

1..

Покажемо, що в цьому випадку цільова функція буде необмеженою на множині своїх планів. Якщо , то з виразу (41) видно, що може приймати довільне додатнє значення, в тому числі . Оскільки значення досліджуваної функції при переході до нового базису збільшується на величину , а , то очевидно, що функція мети буде необмежена також.

2. .

З виразу (41) визначається лише одним способом, а саме

(42)

Якщо б визначалась неоднозначно, то в базисному плані, до якого ми переходимо, було б менше, ніж додатніх компонент, що суперечить припущенню про невиродженість. Якщо визначити з -го рівняння і підставити його значення в інші рівняння області та в цільову функцію, отримаємо новий базисний план , який буде відрізнятися від попереднього базисного плану лише тим, що замість базисної змінної буде змінна . Тобто стає вільною змінною, а вільна змінна – базисною. Значення досліджуваної цільової функції при цьому збільшиться на величину . -товий стовбець, який вводиться в базис на текучій ітерації, називається розв’язковим. Індекс r, що задається співвідношенням (42) визначає розв’язковий рядок.

Елемент , що стоїть на перетині розв’язкового стовбця та розв’язкового рядка називається розв’язковим елементом.

Переходом від одного базисного плану до іншого отримаємо послідовність базисів, а отже послідовність впорядкованих базисних розв’язків з монотонно зростаючим значенням цільової функції задачі (34). Оскільки число можливих базисів скінченне і ні один із базисів не може повторюватись, то за скінченне число кроків отримуємо розвязок задачі (34).

З метою застосування прямого симплекс методу у практичних задачах опишемо його алгоритм.

Нехай задана задача лінійного програмування:

Нехай rang. Наведемо кроки алгоритму

1. Будуємо початковий базисний план . Опишемо перехід від .

2. Для кожного () обчислюємо оцінку:

.

3. Перевіряємо чи

4. Перевіряємо чи є в початковому базисному плані додатні значення. Якщо , то – оптимальний базисний план.

5. Знаходимо . Тоді -товий стовбець буде розв’язковим стовбцем, а змінну слід ввести в базу. Необхідно зауважити, що за розв’язковий стовбець можна вибрати будь-який стовбець, для якого . Однак, зважаючи на те, що значення цільової функції змінюється на величину 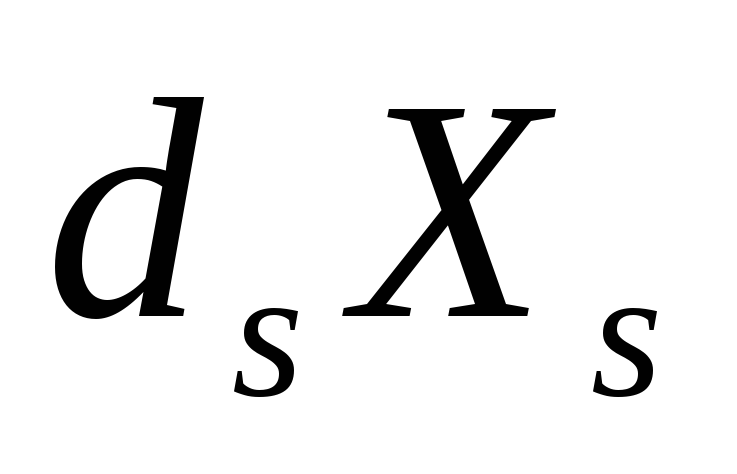, за розв’язковий стовбець доцільно взяти той, якому відповідає найменша оцінка.

6. Нехай , де елементи розв’язкового стовбця. Якщо для то лінійна форма вихідної задачі необмежена на множині планів, в протилежному випадку 7.

7. Нехай . Складаємо відношення елементів стовбця вільних членів до додатніх елементів розв’язкового стовбця і знаходимо серед них мінімальне, а саме:

.

Якщо мінімум досягається при , то це означає що - та змінна виводиться з числа базисних змінних ( - та стрічка розв’язкова), а - розв’язковий елемент.

8. Здійснюємо перехід до нового базисного плану (базис плану отримуємо заміною вектора вектором у попередньому плані). Перехід до нового базису здійснюємо при допомозі формул:

Стовбець вільних членів перераховуємо так:

Елементи матриці умов задачі знаходимо так:

Значення лінійної форми в новому базисі запишеться:

Елементи вектора оцінок шукаємо за формулами:

9. Переходимо до пункту 3 збільшивши індекс ітерації на 1.

Кожен перехід до нового базису називається ітерацією симплексного методу. Описуючи теоретичні основи симплексного методу ми показали, що цей ітераційний процес є скінченним, а отже, за скінченне число кроків ми отримаємо розв’язок ЗЛП, або покажемо, що його не існує через необмеженість цільової функції або несумісність умов задачі

При розв’язуванні ЗЛП на можна:

1. Від задачі на 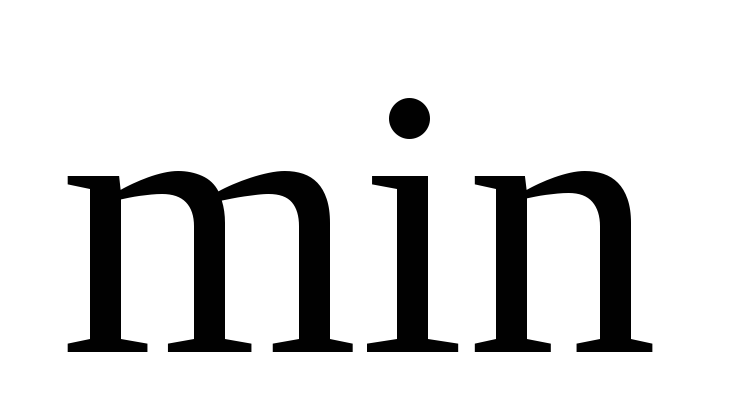перейти до задачі на помінявши знаки коефіцієнтів лінійної форми на протилежні.

2. Розв’язувати ЗЛП на використовуючи описаний вище алгоритм для задачі на , за виключенням того, що:

а) критерієм оптимальності плану при розв’язуванні задачі на служить умова:, ;

б) за розв’язковий стовбець вибираємо той стовбець, якому відповідає максимальна додатня оцінка

Приклад.Розв’яжемо з допомогою прямого алгоритму прямого симплекс-методу задачу лінійного програмування:

,

(43)

Запишемо цю задачу в канонічному вигляді, отримаємо:

,

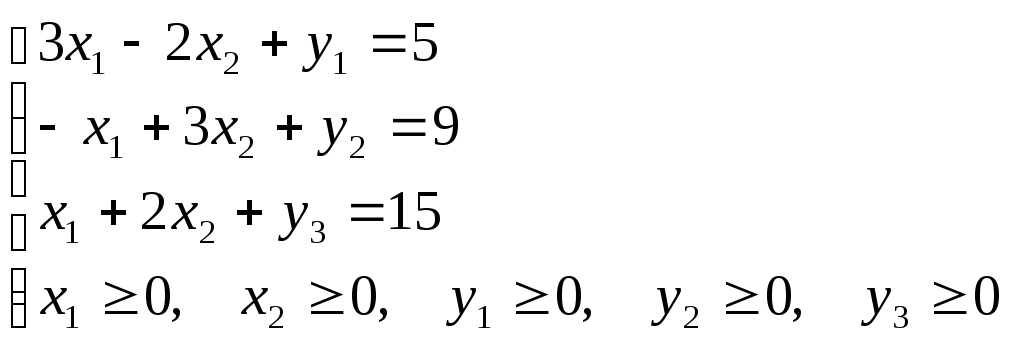(44)

Для цієї задачі початковий базисний план запишеться:

; . (45)

Застосуємо для ілюстрації симплек-методу табличний спосіб. Для кожної задачі, на кожну ітерацію складається нова симплекс-таблиця. Всі таблиці мають однакову структуру.

Запишемо початкову симплекс-таблицю:

Табл.2. Початкова симплекс таблиця для задачі (43).

			2	-1	0	0	0
0		5	3	-2	1	0	0
0		9	-1	3	0	1	0
0		15	1	2	0	0	1
Індексний рядок		0	-2	1	0	0	0

Симплексна таблиця будується для ЗЛП в канонічній формі, вона включає стовбець базисних змінних, стовбець вільних членів, стовбець коефіцієнтів, з якими базисні змінні входять в цільову функцію, а також стовбці коефіцієнтів при всіх невідомих з області обмежень . Важлива роль в симплексній таблиці відводиться індексній стрічці, в якій розміщено вектор оцінок , .

Для нашого прикладу , тому , а саме . Кожен студент повинен вміти прочитати та проаналізувати симплекс-таблицю, а саме:

1). Прочитати базисний план, що відповідає даній симплекс-таблиці. Для цього базисним змінним надають значення із стовбця вільних членів, вільні змінні – рівні нулю.

2). Дати відповідь на запитання чи є даний базисний план оптимальним (проаналізувати чи серед оцінок виконується ).

В наведеному прикладі початковий базисний план (45) не є оптимальним, оскільки . Тому вибираємо перший стовбець за розв’язковий², тобто змінну вводимо в число базисних змінних. Для знаходження розв’язкової стрічки розглядаємо згідно алгоритму співвідношення , це означає, що змінну виводимо з числа базисних і перший рядок є розв’язковим (оскільки співвідношення досягається для першого рядка). Таким чином розвязковий елемент . Здійснивши симплекс перетворення, за формулами кроку 8 алгоритму, відносно розвязкового елемента, отримаємо наступну симплекс таблицю.

Табл.3 Перша симплекс-таблиця для задачі (43).

			2	-1	0	0	0
2		5/3	1	-2/3	1/3	0	0
0		32/3	0	7/3	1/3	1	0
0		40/3	0	8/3	-1/3	0	1
Індексний рядок		10/3	0	-1/3	2/3	0	0

Цій симплекс-таблиці відповідає план:

, . (46)

Оскільки в індексній стрічці є від’ємне значення, то це означає, що план (46) не оптимальний. Другий стовбець отриманої таблиці вибираємо за розв’язковий , тобто змінну вводимо в число базисних. Знаходимо , тобто змінну виводимо з числа базисних. Значення розв’язкового елемента . В результаті симплексного перетворення відносно розв’язкового елемента отримаємо другу симплексну таблицю.

Табл.4. Друга симплекс-таблиця для задачі (43).

			2	-1	0	0	0
2		33/7	---	---	---	---	---
-1		32/7	---	---	---	---	---
0		8/7	---	---	---	---	---
Індексний рядок		34/7	0	0	5/7	1/7	0

В індексній стрічці останньої симплекс-таблиці немає від’ємних оцінок. Це означає, що план оптимальний:

.

У зв’язку із цим симплекс-таблиця порахована не повністю. Максимальне значення цільової функції рівне .

1 Номери введених в задачу доповнюючих та штучних змінних залежать від номерів обмежень до яких вони додаються.

2 У таблиці 2 елементи першого стовбця виділено