16

Лінійне програмування

1.1. Постановка задачі лінійного програмування

В найзагальнішому виді задача лінійного програмування формулюється так:

треба знайти значення n змінних x₁,x₂,…,x_n, які задовільняють системі співвідношень типу:

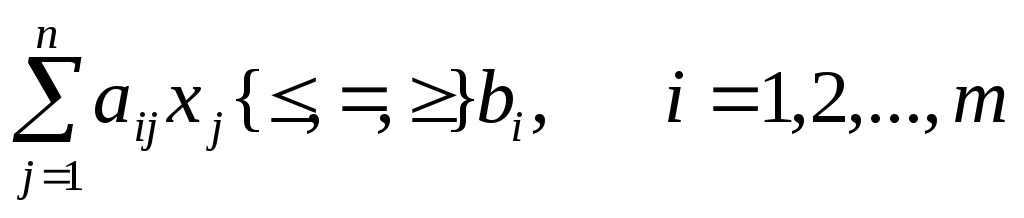(2)

(3)

і при цьому визначають найбільше (найменше) значення функції

(1)

Тут a_ij, b_i, c_j - задані дійсні числа. Крім того, в кожному із співвідношень (2) може використовуватись лише один із знаків ≤, =, ≥ , хоч різні співвідношення можуть мати різні знаки.

Співвідношення (умови) (2), (3) називаються обмеженнями, а функція (1) - цільовою функцією задачі. Суттєвим є те, що ліві частини всіх обмежень (2) - (3) і функція (1) є лінійними відносно змінних x₁,x₂,…,x_n. Якраз через це задачу (1)-(3) називають задачею лінійного програмування (ЗЛП).

Будь-який впорядкований набір (вектор) (x₁⁰,x₂⁰,…,x_n⁰) значень змінних, який задовільняє всім обмеженням (2)-(3) (тобто, будь-який розв‘язок системи лінійних рівнянь і нерівностей (2)-(3)), називається допустимим розв'язком або планом задачі.

Допустимий розв‘язок задачі лінійного програмування, який оптимізує (максимізує або мінімізує) її цільову функцію, називається оптимальним розв'язком (оптимальним планом) задачі.

Приклад: Нехай дана задача лінійного програмування:

знайти максимум функції L = -8 x₁+x₂+4x₃ - x₄

при обмеженнях:

2 x₁+x₂ - x₃+x₄≤8

- x₁+x₂+8x₃ - 2x₄≥6

x₁ -2x₂+3x₃ - x₄=2

Легко перевірити, що такі, наприклад, набори x₁=1, x₂=1, x₃=1, x₄=0 та x₁=0, x₂=2, x₃=2, x₄=0 значень невідомих є допустимими розв'язками даної задачі, тому що задовільняють обмеження. А, наприклад, набір x₁=1, x₂=0, x₃=2, x₄=-1 не є допустимим розв'язком задачі, оскільки не задовільняються третє обмеження і обмеження на знак змінної х₄.

Знайдемо значення цільової функції для відповідних допустимих розв'язків.

Для першого маємо:

L=-8*1+1*1+4*1-1*0= -3

для другого:

L=-8*0+1*2+4*2-1*0= 10

Оскільки значення цільової функції для першого допустимого розв'язку є менше, ніж значення цільової функції для другого допустимого розв'язку, то зрозуміло, що перший допустимий розв'язок не є оптимальним розв'язком даної задачі. Що стосується другого допустимого розв'язку, то без додаткового дослідження не можна сказати чи є він оптимальним розв'язком задачі, чи ні.

Зрозуміло, що не кожна задача лінійного програмування має допустимий розв'язок, тому що не кожна система рівнянь і нерівностей має розв'язок. Задачу, яка не має жодного допустимого розв'язку, будемо називати нерозрішимою через несумісність умов.

Виявляється теж, що не для всякої задачі, яка має допустимі розв'язки, існує оптимальний розв'язок. Такі задачі будемо називати нерозрішимими через необмеженість цільової функції.

1.2.Приклади економічних задач лінійного програмування

Задача про найкраще використання ресурсів.

Нехай деяке підприємство має в своєму розпорядженні ресурси різних видів - сировину, робочу силу, обладнання тощо (і=1,2,...,т - індекс виду ресурсу). Кількості ресурсів відповідно рівні b_i - (і=1,2,...,т). На основі цих ресурсів можна випускати п видів продукції (j=1,2,...,n - індекс виду продукції). Прибуток від реалізації одиниці продукції j-гo виду дорівнює p_j (j=1,2,...,n). Відомі також необхідні кількості витрат і-го ресурсу на виробництво одиниці продукції j-гo виду - a_ij. Необхідно визначити такі обсяги випуску продукції кожного виду x_j (j=1,2,...,n), які б забезпечували отримання максимального прибутку при заданих обмеженнях на використовувані ресурси.

Введені позначення дозволяють побудувати математичну модель даної задачі. Оскільки p_j прибуток від реалізації одиниці продукції j-го виду, то x_j одиниць забезпечують p_jx_j одиниць прибутку. Загальний прибуток (позначимо його через Р) буде рівним Р=р₁х₁ + р₂х₂+…+р_пх_п

Отриманий вираз є цільовою функцією задачі.

Сформулюємо систему обмежень. Очевидно a_ijх_j - витрати і-го ресурсу на виробництво х_j одиниць продукції j-го виду. Підсумувавши витрату і-го ресурсу на випуск всіх видів продукції, отримаємо загальну витрату цього ресурсу. Вона не повинна перевищувати об‘єму b_i (і=1,2,...,т), тобто

а₁₁х₁+ а₁₂х₂+…+ а_1пх_п ≤ b₁

а₂₁х₁+ а₂₂х₂+…+ а_2пх_п ≤ b₂

………………………………

а_т1х₁+ а_т2х₂+…+ а_тпх_п ≤ b_m .

Щоб шуканий план виробництва був реальним, необхідно вказати, що обсяги випуску продукції кожного виду повинні бути невід‘ємні, тобто

Таким чином задача про найкраще використання ресурсів в компактному записі матиме вигляд:

,

і є, очевидно, типовою задачею лінійного програмування.

Приклад: Для виготовлення двох видів продукції П₁ і П₂ використовують три види сировини С₁, С₂, С₃. Запаси сировини, кількість одиниць сировини, які витрачаються на виготовлення одиниці продукції кожного виду, а також величина прибутку від реалізації одиниці продукції, наведені в таблиці:

Табл.1. Вихідні умови задачі.

Вид сировини	Кількість одиниць сировини, які витрачаються на 1 од. продукції		Запас сировини
	П1	П2
С1	1	5	15
С2	4	5	20
С3	10	2	35
Прибуток від реалізації одиниці продукції	20	10

Позначимо через х₁ кількість одиниць продукції П₁ а через х₂ - кількість одиниць продукції П_2, яку ми будемо виготовляти. Тоді, враховуючи кількість одиниць сировини, які витрачаються на виробництво одиниці продукції кожного виду, а також запаси сировини, отримаємо систему обмежень:

х₁+ 5х₂ ≤ 15

4х₁+ 5х₂ ≤ 20

10х₁+ 2х₂ ≤ 35

x₁ ≥0, x₂ ≥0,

яка показує, що кількість сировини, яка витрачається на виготовлення продукції, не може перевищити наявних запасів, а також те, що випуск продукції не може бути від‘ємною величиною.

Кінцеву ціль задачі - отримання максимального прибутку від реалізації (а ми приймаємо , що вся випущена продукція реалізується) - виразимо як функцію двох змінних х₁ і х₂. Реалізація х₁ одиниць продукції дає прибуток 20х₁ грн., х₂ одиниць продукції П₂ - прибуток 10х₂ а, отже, сумарний прибуток Р буде рівний 20х₁ + 10х₂. Тоді задача оптимального використання сировини полягатиме у відшуканні таких невід‘ємних значень х₁ і х₂ при яких прибуток Р буде максимальним за умови не перевищення витрат сировини (ресурсів) над їх запасами:

max P = 20х₁ + 10х₂

х₁+ 5х₂ ≤ 15

4х₁+ 5х₂ ≤ 20

10х₁+ 2х₂ ≤ 35

x₁ ≥0, x₂ ≥0.