12.9. Линейные однородные дифференциальные уравнения с постоянными коэффициентами

Характеристическое уравнение. Если в уравнении (34) коэффициенты постоянные, то оно называется линейным однородным уравнением с постоянными коэффициентами и имеет вид

(37),

где все вещественные числа, у – искомая функция, х – независимая переменная.

Решение этого уравнения ищется в виде . Это приводит к алгебраическому уравнению степени n (38), которое называется характеристическим.

Таким образом, чтобы составить характеристическое уравнение (39) надо в уравнении (37) заменить производные степенями неизвестной величины k, причем степень k должна быть равна порядку соответствующей производной, а сама искомая функция у заменена 1.

I. Если все корни характеристического уравнения числа вещественные и среди них нет равных между собой, то представляя значение корней в (*) получим n частных линейно независимых решений уравнения (37) в виде (**)

II. Если все корни характеристического уравнения числа вещественные, но среди них есть равные, то каждому корню кратности , соответствует линейно независимых частных решений уравнения (37) .

III. Если среди корней характеристического уравнения имеются комплексные, но не равные между собой, то каждой паре сопряженных комплексных корней и соответствует два частных линейно независимых решений уравнения (37) вида и (***)

Если же среди комплексных корней характеристического уравнения имеются кратные комплексные корни, то корню кратности (корень имеет ту же кратность) соответствует частных линейно независимых решений уравнения (37), которые имеют вид

В заключение приведем схему решения линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами:

1) Составляем характеристическое уравнение

2) Находим корни характеристического уравнения

3) В зависимости от характера корней выписываем частные линейно независимые решения дифференциального уравнения

4) Подставляя их в формулу , получаем общее решение дифференциального уравнения (37)

Пример 15. Найти общее решение уравнения

Составим характеристическое уравнение , его можно переписать в виде и найти его корни , им соответствуют решения

Общее решение имеет вид: .

12.10. Линейные неоднородные дифференциальные уравнения

Предполагается, что функции и правая часть уравнения – функция непрерывны в промежутке (a, b), случаи не исключаются. Функции называются коэффициентами уравнения.

1. Линейное неоднородное дифференциальное уравнение имеет вид

(40)

2. Общее решение линейного неоднородного уравнения находится так:

а) Найти одно какое-нибудь его частное решение

б) Найти общее решение соответствующего однородного уравнения

в) Сложить эти два решения. Сумма их и будет общим решением уравнения (40)

Так, если частное решение неоднородного уравнения есть Y, а общее решение соответствующего однородного есть , то общее решение линейного неоднородного уравнения (40) (41)

3. Если правая часть уравнения (40) есть сумма двух функций

(42)

Следует рассматривать два уравнения, у которых левые части такие же, как в (42), нов одном из них правой частью будет функция , а во втором , т.е. рассмотреть уравнение

(43)

(44)

Если функции и - соответственно частные решения уравнений (43) и (44), то их сумма будет частным решением (42) (это свойство называется положением решений и распространяется на случай, когда правая часть – сумма n решений)

4. Если известно общее решение однородного линейного уравнения, соответствующего заданному неоднородному, то его частное решение Y можно найти с помощью квадратур методом, который указал Лагранж. Этот метод называется методом вариации (изменения) произвольных постоянных.

Получив общее решение соответствующего однородного уравнения , поступают так: полагают, что в этом решении величины являются не постоянными, а функциями независимой переменной х. Записывают это так:

Для определения функций составляется система уравнений:

(45)

Рассмотрим подробно этот метод для линейных дифференциальных неоднородных уравнений второго порядка (46)

Получив особое решение (47) соответствующего однородного уравнения поступают так: полагают, что в этом решении величины и являются не постоянными, а функциями независимой переменной х и записывают

Для определения функций и составляется система (45)

(48)

Определитель этой системы – определитель Вронского; так как (47) есть общее решение (46), то функции и линейно независимы и их определитель не равен 0. Поэтому система (48) имеет всегда решение и притом единственное.

Решая эту систему уравнений относительно и , получим:

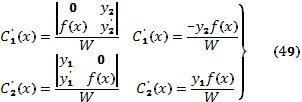
Где определитель Вронского

Из (49) интегрированием находим

Подставляя (50) в (47) получим

Раскрывая скобки, найдем

Сравнивая с (41) замечаем, что первые два слагаемых в правой части – общее решение однородного уравнения, соответствующего (46), а последние два слагаемых – частное решение неоднородного уравнения (46)

Обозначая эти два слагаемых через Y, получаем формулу частного решения линейного неоднородного уравнения второго порядка

В более компактной форме частное решение линейного неоднородного уравнения второго порядка может быть записано так:

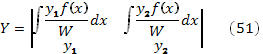
Все величины, входящие в эту формулу известны.

Замечание 9. Следует иметь в виду, что система (48) так же, как и формула (51), имеет место тогда, когда коэффициент при старшей производной равен единице. Функция есть правая часть уравнения при этом предположении.

Метод вариации произвольных постоянных – универсальный. Он позволяет при помощи квадратур определить частное решение линейного неоднородного дифференциального уравнения (34), если известно общее решение соответствующего ему однородного уравнения.

Пример 16. Проинтегрировать уравнение

Корни характеристического уравнения комплексные сопряженные , следовательно, общее решение однородного уравнения есть

Общее решение неоднородного уравнения ищем в виде , так как для данного примера , составляем систему

Из этой системы найдем функции и

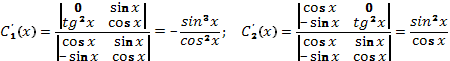
Подставив найденные значения и , получим общее решение данного дифференциального уравнения: