
- •Глава 12. Элементы теории обыкновенных дифференциальных уравнений (оду)
- •12.1 Основные понятия и определения
- •12.2 Дифференциальные уравнения с разделяющимися переменными
- •12.3 Однородные и квазиоднородные уравнения
- •12.4 Линейные дифференциальные уравнения первого порядка
- •12.5 Дифференциальные уравнения в полных дифференциалах
- •12.6. Уравнения, не разрешенные относительно производной
- •12.7. Дифференциальные уравнения высших порядков
- •12.7.1 Основные понятия. Теорема Коши.
- •12.7.2. Уравнения, допускающие понижения порядка.
- •12.8. Линейные дифференциальные уравнения высших порядков
- •12.9. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •12.10. Линейные неоднородные дифференциальные уравнения
- •12.11. Метод неопределенных коэффициентов для определения частного решения неоднородного линейного уравнения с постоянными коэффициентами
- •12.12. Уравнение Эйлера. Системы линейных дифференциальных уравнений с постоянными коэффициентами (основные понятия)
- •12.13. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами
- •12.14. Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •12.15. Понятие решения
- •12.16. Уравнения с разделяющимися коэффициентами
- •12.17. Однородные уравнения
- •12.18. Линейные уравнения первого порядка
- •12.19. Уравнение Бернулли
- •12.20. Уравнения в полных дифференциалах
- •12.21. Уравнения вида
- •12.22. Уравнения вида
- •12.23. Линейные уравнения с постоянными коэффициентами
- •12.24. Принцип суперпозиции
- •12.25. Метод Лагранжа
- •Вопросы, упражнения и задачи к главе «Дифференциальные уравнения»
- •Тест для самоконтроля к главе «Дифференциальные уравнения»
12.7. Дифференциальные уравнения высших порядков
12.7.1 Основные понятия. Теорема Коши.
Дифференциальное уравнение n-го порядка имеет вид
![]() или
или ![]()
Задачей Коши для
дифференциального уравнения (19) называется
задача отыскания решения ![]() ,
удовлетворяющего заданным начальным
условиям.
,
удовлетворяющего заданным начальным
условиям.
![]()
Общим решением
уравнения (18) или (19) называется такая
функция ![]() ,
которая при любых допустимых значениях
параметров
,
которая при любых допустимых значениях
параметров ![]() является решением этого дифференциального
уравнения и для любой задачи Коши с
условиями (20) найдутся постоянные
является решением этого дифференциального
уравнения и для любой задачи Коши с
условиями (20) найдутся постоянные ![]() , определяемые из системы уравнений:
, определяемые из системы уравнений:
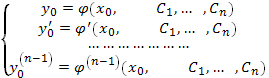
Уравнение 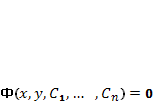 ,
определяющее общее решение как неявную
функцию, называется общим интегралом
дифференциального уравнения.
,
определяющее общее решение как неявную
функцию, называется общим интегралом
дифференциального уравнения.
Теорема существования и единственности решения задачи Коши.
Если дифференциальное
уравнение (19) таково, что функция ![]() в некоторой области D
изменения своих аргументов непрерывна
и имеет непрерывные частные производные
в некоторой области D
изменения своих аргументов непрерывна
и имеет непрерывные частные производные
![]() , то для любой точки
, то для любой точки ![]() существует такой интервал
существует такой интервал ![]() ,
на котором существует и притом
единственное решение этого уравнения,
удовлетворяющее начальным условиям
(20).
,
на котором существует и притом
единственное решение этого уравнения,
удовлетворяющее начальным условиям
(20).
12.7.2. Уравнения, допускающие понижения порядка.
Уравнения, содержащие только производную порядка n и независимую переменную.
Эти уравнения
имеют вид: ![]() .
.
Если удаётся это
уравнение разделить относительно ![]() ,
то оно записывается так:
,
то оно записывается так: ![]() .
.
Общее решение имеет вид: (22)
Из этого видно,
что для получения общего решения
уравнения (21) нужно n-раз
проинтегрировать функцию ![]() и прибавить к полученному результату
многочлен от х
степени (n-1),
коэффициентами которого являются
произвольные постоянные.
и прибавить к полученному результату
многочлен от х
степени (n-1),
коэффициентами которого являются
произвольные постоянные.
Если задача Коши решается для уравнения (21) с начальными условиями, то частное решение уравнения (21) примет вид:
![]()
Пример 12.
Найти общее решение уравнения ![]() и его частное решение, удовлетворяющее
начальным условиям
и его частное решение, удовлетворяющее
начальным условиям ![]() .
.
Интегрируя первый
раз, получаем ![]() .
Повторное интегрирование дает:
.
Повторное интегрирование дает: ![]() .
.
Это и есть общее
решение. Подставив теперь в полученное
общее решение и в выражение для первой
производной ![]() и соответственно
и соответственно ![]() получим систему двух уравнений с
неизвестными
получим систему двух уравнений с
неизвестными ![]() и
и ![]() .
Решив ее, найдем значения параметров
.
Решив ее, найдем значения параметров
![]() и
и ![]() ,
соответствующие искомому частному
решению, которое, следовательно, имеет
вид
,
соответствующие искомому частному
решению, которое, следовательно, имеет
вид ![]() .
.
Второй тип: Уравнения, не содержащие искомой функции.
Уравнение порядка n, не содержащее искомой функции, имеет такой вид:
![]() (23)
(23)
Порядок его может
быть понижен на единицу с помощью
подстановки ![]() (24), где
(24), где ![]() - новая функция. Эта подстановка приводит
к уравнению
- новая функция. Эта подстановка приводит
к уравнению ![]() (25)
(25)
Если уравнение
(22) не содержит ни искомой функции у,
ни ее производных до порядка (k-1)
включительно, т.е. имеет вид ![]() (26),то его порядок может быть понижен на
k
единиц при помощи подстановки
(26),то его порядок может быть понижен на
k
единиц при помощи подстановки ![]() .
.
После определения
функции ![]() уравнение (26) оказывается приведенным
к виду уравнения (21). К этому же типу
уравнений относятся и такие, которые
содержат только две последовательные
производные, т.е. уравнения вида
уравнение (26) оказывается приведенным
к виду уравнения (21). К этому же типу
уравнений относятся и такие, которые
содержат только две последовательные
производные, т.е. уравнения вида ![]() .
Если это уравнение можно решить
относительно
.
Если это уравнение можно решить
относительно ![]() ,
то оно принимает вид
,
то оно принимает вид ![]() и интегрируется подстановкой
и интегрируется подстановкой ![]() (27), которая приводит к уравнению
(27), которая приводит к уравнению ![]() .
Определив из этого уравнения функцию
.
Определив из этого уравнения функцию
![]() и подставив ее в (27) придем к уравнению
(21).
и подставив ее в (27) придем к уравнению
(21).
Пример 13.
![]() подстановка
подстановка ![]()
![]() ,
а это уравнение с разделяющимися
переменными.
,
а это уравнение с разделяющимися
переменными.
![]()
![]()
Проверяем на особые
решения (мы делили на ![]() и могли потерять)
и могли потерять)
![]()
![]() - особое решение.
- особое решение.
Третий тип: Уравнения, не содержащие независимой переменной.
Эти уравнения
имеют в общем случае такой вид: ![]() (28)
(28)
Понижение порядка
на единицу достигается подстановкой
![]() ,
где
,
где ![]() - новая искомая функция. В этом случае
за независимую переменную принимается
не х,
а у.
Поэтому вторая и последующие производные
должны быть преобразованы так, чтобы
независимой переменной была у.
- новая искомая функция. В этом случае
за независимую переменную принимается
не х,
а у.
Поэтому вторая и последующие производные
должны быть преобразованы так, чтобы
независимой переменной была у.
![]() ,
так как
,
так как ![]()
![]() (29)
(29)
Поэтому уравнение
(28) перепишется так: ![]()
Если удается найти
общее решение этого уравнения, то оно
будет иметь вид: ![]() (30)
(30)
Так как ![]() ,
то (30) – уравнение первого порядка, из
которого определится искомая функция
у.
,
то (30) – уравнение первого порядка, из
которого определится искомая функция
у.
Частный случай.
Если уравнение
(28) имеет вид ![]() (31) и его удается разрешить относительно
y’’
так, что
(31) и его удается разрешить относительно
y’’
так, что ![]() (32), то интегрирование кроме указанного
приема можно провести так: умножим обе
части на и приведем уравнение к виду
(32), то интегрирование кроме указанного
приема можно провести так: умножим обе
части на и приведем уравнение к виду
(33)
Левая часть этого
уравнения 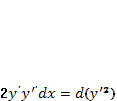 ,
а в правой части
,
а в правой части ![]() ,
поэтому (33) перепишется так:
,
поэтому (33) перепишется так:
![]() ,
отсюда
,
отсюда ![]() ,
,
![]()
Последнее уравнение допускает разделение переменных, проинтегрировав его, найдем:
![]() , т.е. определим х
как функцию от у.
, т.е. определим х
как функцию от у.
Следует отметить, что этот прием интегрирования уравнения (31) не дает ничего существенно нового по сравнению с указанным общим приемом замены y’’ по формулам (29).
Замечание 8.
К уравнению вида (31) приводятся также
и уравнения вида ![]() ,
содержащие только две производные,
порядки которых отличаются на две
единицы. В этом случае применяется
подстановка
,
содержащие только две производные,
порядки которых отличаются на две
единицы. В этом случае применяется
подстановка ![]() .
.
Пример 14.
Найти общий интеграл уравнения ![]() .
.
Пусть ![]() ,
тогда по формулам (29)
,
тогда по формулам (29) ![]() ,
тогда уравнение перепишется так
,
тогда уравнение перепишется так ![]() , разделяя переменные, получаем
, разделяя переменные, получаем ![]() (произвольную постоянную мы ввели под
видом с тем, чтобы в последующем извлечь
корень из 4)
(произвольную постоянную мы ввели под
видом с тем, чтобы в последующем извлечь
корень из 4)
![]() , так как
, так как ![]() , последнее уравнение перепишется так:
, последнее уравнение перепишется так:
![]() . Разделяя переменные, получаем
. Разделяя переменные, получаем ![]() .
Интегрируя, получаем ,
.
Интегрируя, получаем , ![]() ,
окончательно получаем:
,
окончательно получаем:
![]() .
.
