
- •Глава 12. Элементы теории обыкновенных дифференциальных уравнений (оду)
- •12.1 Основные понятия и определения
- •12.2 Дифференциальные уравнения с разделяющимися переменными
- •12.3 Однородные и квазиоднородные уравнения
- •12.4 Линейные дифференциальные уравнения первого порядка
- •12.5 Дифференциальные уравнения в полных дифференциалах
- •12.6. Уравнения, не разрешенные относительно производной
- •12.7. Дифференциальные уравнения высших порядков
- •12.7.1 Основные понятия. Теорема Коши.
- •12.7.2. Уравнения, допускающие понижения порядка.
- •12.8. Линейные дифференциальные уравнения высших порядков
- •12.9. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •12.10. Линейные неоднородные дифференциальные уравнения
- •12.11. Метод неопределенных коэффициентов для определения частного решения неоднородного линейного уравнения с постоянными коэффициентами
- •12.12. Уравнение Эйлера. Системы линейных дифференциальных уравнений с постоянными коэффициентами (основные понятия)
- •12.13. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами
- •12.14. Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •12.15. Понятие решения
- •12.16. Уравнения с разделяющимися коэффициентами
- •12.17. Однородные уравнения
- •12.18. Линейные уравнения первого порядка
- •12.19. Уравнение Бернулли
- •12.20. Уравнения в полных дифференциалах
- •12.21. Уравнения вида
- •12.22. Уравнения вида
- •12.23. Линейные уравнения с постоянными коэффициентами
- •12.24. Принцип суперпозиции
- •12.25. Метод Лагранжа
- •Вопросы, упражнения и задачи к главе «Дифференциальные уравнения»
- •Тест для самоконтроля к главе «Дифференциальные уравнения»
12.4 Линейные дифференциальные уравнения первого порядка
Уравнение вида
![]() (8) называется линейным (
у и у
‘ входят в первых степенях, не перемножаясь
между собой).
(8) называется линейным (
у и у
‘ входят в первых степенях, не перемножаясь
между собой).
Если ![]() , то это уравнение называется линейным
неоднородным, а если
, то это уравнение называется линейным
неоднородным, а если ![]() - линейным однородным.
- линейным однородным.
Общее решение
однородного уравнения легко получается
разделением переменных; разделяя
переменные в уравнении ![]() ,
находим последовательно
,
находим последовательно
![]() ,
или, наконец,
,
или, наконец, ![]() ,
где С – произвольная постоянная.
,
где С – произвольная постоянная.
Общее решение неоднородного линейного уравнения можно найти исходя из общего решения соответствующего однородного уравнения по методу Лагранжа,
(Жозеф Луи Лагранж (1736-1813) родился в Турине в итало-французской семье. 19 лет от роду он стал профессором математики артиллерийской школы в Турине. Создатель вариационного исчисления. Наиболее значительный труд «Аналитическая механика»)
варьируя произвольную
постоянную, т.е. полагая ![]() ,
где
,
где ![]() – некоторая, подлежащая определению,
дифференцируемая функция от х.
Для нахождения
– некоторая, подлежащая определению,
дифференцируемая функция от х.
Для нахождения ![]() подставляем у
в исходное уравнение, что приводит к
уравнению
подставляем у
в исходное уравнение, что приводит к
уравнению ![]() , отсюда
, отсюда ![]() ,
где С – произвольная постоянная.
,
где С – произвольная постоянная.
Тогда искомое
общее решение неоднородного уравнения
будет иметь вид ![]() .
.
Линейные уравнения первого порядка можно интегрировать также методом Бернулли, который заключается в следующем.
Полагая ![]() , где u,
v
– две неизвестные функции, преобразуем
исходное уравнение к виду
, где u,
v
– две неизвестные функции, преобразуем
исходное уравнение к виду ![]() или
или ![]() .
.
Пользуясь тем. Что
одна из неизвестных функций (например
v)
может быть выбрана совершенно произвольно
(поскольку лишь произведение ![]() должно удовлетворять исходному уравнению)
принимают за v
любое частное решение уравнения
должно удовлетворять исходному уравнению)
принимают за v
любое частное решение уравнения ![]() (например,
(например, ![]() ),
обращающее, следовательно, в нуль
коэффициент при u
в последнем уравнении.
),
обращающее, следовательно, в нуль
коэффициент при u
в последнем уравнении.
Предыдущее
уравнение приведется тогда к уравнению
![]() или
или ![]() ,
из которого находим u:
,
из которого находим u:
![]() .
Умножая u
на v,
находим для
решения исходного уравнения прежнее
выражение
.
Умножая u
на v,
находим для
решения исходного уравнения прежнее
выражение ![]() .
.
Замечание 4.
На практике поступают следующим образом:
вводят подстановку ![]() (9). Эта подстановка (9) приводит уравнение
(8) к уравнению с разделяющимися
переменными.
(9). Эта подстановка (9) приводит уравнение
(8) к уравнению с разделяющимися
переменными.
Пример 5.
Решить дифференциальное уравнение
![]() .
.
![]()
Значит, делаем
подстановку ![]() +
+
![]() , а сокращая на
, а сокращая на ![]() и разделяя переменные
и разделяя переменные ![]() .
Возвращаясь к подстановке
.
Возвращаясь к подстановке ![]() .
.
Другой способ (метод Лагранжа)
![]()
Ищем решение
соответствующего однородного уравнения
![]()
![]() делим на y
делим на y
![]() => интегрируя, получаем
=> интегрируя, получаем
![]() =>
=> ![]() (
(![]() обозначим вновь через С)
обозначим вновь через С)
![]()
Ищем решение
исходного неоднородного уравнения в
виде ![]() ,
где
,
где ![]() - неизвестная функция. Подставляя в
исходное уравнение
- неизвестная функция. Подставляя в
исходное уравнение
![]()
Сокращая на ![]() ,
,
![]() ,
подставляя это значение в (*), получаем
,
подставляя это значение в (*), получаем
![]() .
.
Уравнение вида
![]() называется уравнением Бернулли, так
как
называется уравнением Бернулли, так
как ![]() (при
(при ![]() уравнение является линейным, а при
уравнение является линейным, а при ![]() - уравнение с разделяющимися переменными).
- уравнение с разделяющимися переменными).
После умножения
его обеих частей на ![]() и подстановки
и подстановки ![]() ,
где z
– новая искомая функция, оно приводится
к линейному.
,
где z
– новая искомая функция, оно приводится
к линейному.
Преобразование уравнения Бернулли в линейное будем проводить в такой последовательности:
1) Умножим обе части
уравнения на ![]()
2) Введем подстановку
![]() .
Обе части этого равенства продифференцируем:
.
Обе части этого равенства продифференцируем:
![]()
3) Полученное
уравнение проинтегрируем как линейное
с помощью подстановки ![]()
4) Возвращаемся к
искомой функции, заменяя z
на ![]() .
.
Пример 6.
![]()
Умножим обе части
на ![]()
![]()
Делаем подстановку
![]()
( делим на 2 )
![]() .
См. предыдущий пример
.
См. предыдущий пример
Общий интеграл
![]() .
Возвращаясь к искомой функции:
.
Возвращаясь к искомой функции:
![]()
Замечание 5.
На практике при решении уравнений
Бернулли их не сводят к линейным, а
интегрируют подстановкой ![]() или методом Лагранжа (метод вариации
произвольной постоянной).
или методом Лагранжа (метод вариации
произвольной постоянной).
Уравнение Риккати
по имени итальянского математика и
инженера Я.Ф.Риккати (1676-1754) называют
ОДУ вида ![]() (*), где
(*), где ![]() – функции, непрерывные в некотором
интервале изменения х.
Это ОДУ содержит в себе частные случаи
уже рассмотренных ранее уравнений: если
– функции, непрерывные в некотором
интервале изменения х.
Это ОДУ содержит в себе частные случаи
уже рассмотренных ранее уравнений: если
![]() ,
то (*) – линейное неоднородное уравнение
ОДУ, а если
,
то (*) – линейное неоднородное уравнение
ОДУ, а если ![]() - уравнение Бернулли с
- уравнение Бернулли с ![]() .
.
К сожалению, решение уравнения Риккати в общем случае не удается свести к операции интегрирования. Однако, если известно одно частное решение ОДУ (*), то его общее решение можно найти при помощи двух последовательных операций интегрирования.
Действительно,
пусть ![]() - частное решение (*), выполнив подстановку
- частное решение (*), выполнив подстановку
![]() получим
получим ![]()
Так как ![]() - решение ОДУ (*), то окончательно имеем
- решение ОДУ (*), то окончательно имеем
![]()
Это уравнение
Бернулли с ![]() .
Заменой
.
Заменой ![]() его можно свести к линейному неоднородному
ОДУ, для нахождения общего решения
которого достаточно выполнить
последовательно две операции
интегрирования.
его можно свести к линейному неоднородному
ОДУ, для нахождения общего решения
которого достаточно выполнить
последовательно две операции
интегрирования.
Пример 7.
Уравнение Риккати ![]()
Имеет частное
решение ![]() .
Замена
.
Замена ![]() приводит его к уравнению Бернулли
Риккати
приводит его к уравнению Бернулли
Риккати ![]() .
Положим
.
Положим ![]() ,тогда
можно записать
,тогда
можно записать
![]()
Приравняв к нулю
коэффициенты при u,
получим ОДУ ![]() ,
имеющее частное решение
,
имеющее частное решение ![]() .
Теперь ОДУ для нахождения
.
Теперь ОДУ для нахождения ![]() принимает вид
принимает вид ![]()
Разделяя переменные
и интегрируя, получаем с учетом потерянного
решения ![]()
![]() и
и ![]() ,
где
,
где ![]() - первообразная функции
- первообразная функции ![]() .
.
В итоге исходное
уравнение Риккати имеет решения 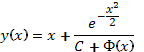 и
и ![]() .
.
Замечание 6. Особых решений уравнение Риккати не имеет.
