
- •Глава 12. Элементы теории обыкновенных дифференциальных уравнений (оду)
- •12.1 Основные понятия и определения
- •12.2 Дифференциальные уравнения с разделяющимися переменными
- •12.3 Однородные и квазиоднородные уравнения
- •12.4 Линейные дифференциальные уравнения первого порядка
- •12.5 Дифференциальные уравнения в полных дифференциалах
- •12.6. Уравнения, не разрешенные относительно производной
- •12.7. Дифференциальные уравнения высших порядков
- •12.7.1 Основные понятия. Теорема Коши.
- •12.7.2. Уравнения, допускающие понижения порядка.
- •12.8. Линейные дифференциальные уравнения высших порядков
- •12.9. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •12.10. Линейные неоднородные дифференциальные уравнения
- •12.11. Метод неопределенных коэффициентов для определения частного решения неоднородного линейного уравнения с постоянными коэффициентами
- •12.12. Уравнение Эйлера. Системы линейных дифференциальных уравнений с постоянными коэффициентами (основные понятия)
- •12.13. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами
- •12.14. Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •12.15. Понятие решения
- •12.16. Уравнения с разделяющимися коэффициентами
- •12.17. Однородные уравнения
- •12.18. Линейные уравнения первого порядка
- •12.19. Уравнение Бернулли
- •12.20. Уравнения в полных дифференциалах
- •12.21. Уравнения вида
- •12.22. Уравнения вида
- •12.23. Линейные уравнения с постоянными коэффициентами
- •12.24. Принцип суперпозиции
- •12.25. Метод Лагранжа
- •Вопросы, упражнения и задачи к главе «Дифференциальные уравнения»
- •Тест для самоконтроля к главе «Дифференциальные уравнения»
12.24. Принцип суперпозиции
Постановка задачи. Найти общее решение линейного дифференциального уравнения -го порядка с постоянными коэффициентами
![]()
где ![]() .
.
Алгоритм решения.
Принцип
суперпозиции. Если
правая часть уравнения (96) есть сумма
нескольких функций ![]() и
и ![]() - какое-нибудь частное решение каздого
уравнения
- какое-нибудь частное решение каздого
уравнения
![]()
то в силу линейности уравнения (96) его общее решение имеет вид
![]()
где ![]() - общее решение однородного уравнения
- общее решение однородного уравнения
![]()
1. Находим
фундаментальную систему решений и общее
решение ![]() однородного уравнения.
однородного уравнения.
2. Для каждого
неоднородного уравнения (97)![]() находим частное решение
находим частное решение ![]() (используя, например, метод подбора или
метод вариации произвольных постоянных).
(используя, например, метод подбора или
метод вариации произвольных постоянных).
Записываем ответ в виде (98).
Пример 30. Найти общее решение линейного дифференциального уравнения
![]()
Решение.
1. Записываем соответствующее однородное уравнение
![]()
и ищем его решение
в виде ![]() ,
где
,
где ![]() - неизвестное число.
- неизвестное число.
Подставляя ![]() и
и ![]() в уравнение (99) и сокращая
в уравнение (99) и сокращая ![]() ,
получаем так называемое характеристическое
уравнение
,
получаем так называемое характеристическое
уравнение
![]()
Характеристическое
уравнение имеет три корня ![]() и
и ![]() .
.
Таким образом, имеем фундаментальную систему решений
![]()
и общее решение однородного уравнения
![]()
2. Решаем неоднородное уравнение, используя принцип суперпозиции:
а) ищем частное
решение ![]() неоднородного уравнения
неоднородного уравнения
![]()
в виде ![]() ,
где А – неопределенный коэффициент (
так как
,
где А – неопределенный коэффициент (
так как ![]() – корень характеристического уравнения
кратности
– корень характеристического уравнения
кратности ![]() ).
).
Дифференцируя ![]() три раза и подставляя в уравнение (100),
находим
три раза и подставляя в уравнение (100),
находим ![]() .
Таким образом,
.
Таким образом,
![]()
б) ищем частное
решение ![]() неоднородного уравнения
неоднородного уравнения
![]()
в виде ![]() ,
где
,
где ![]() и
и ![]() – неопределенные коэффициенты (так как
– неопределенные коэффициенты (так как
![]() не являются корнями характеристического
уравнения, то множитель х
отсутствует).
не являются корнями характеристического
уравнения, то множитель х
отсутствует).
Дифференцируя ![]() три раза и подставляя в уравнение (101),
находим
три раза и подставляя в уравнение (101),
находим ![]() и
и ![]() .
Таким образом,
.
Таким образом,
![]()
Используя принцип суперпозиции (98), получаем
![]()
Ответ. ![]() .
.
Условия задач. Найти общее решение дифференциальных уравнений.
1. ![]() Ответ:
Ответ: ![]()
2. ![]() Ответ:
Ответ: ![]()
12.25. Метод Лагранжа
Постановка задачи. Найти решение задачи Коши для линейного неоднородного уравнения с постоянными коэффициентами
![]()
с начальными условиями
![]()
Алгоритм решения.
1. Записываем соответствующее однородное уравнение с постоянными коэффициентами
![]()
Находим фундаментальную
систему решений ![]() и
и ![]() и общее решение однородного уравнения
и общее решение однородного уравнения
![]()
2. Применяем метод Лагранжа (метод вариации произвольных постоянных).
Если известна
фундаментальная система решений ![]() и
и ![]() однородного уравнения (103), то общее
решение соответствующего неоднородного
уравнения (102) может быть найдено по
формуле
однородного уравнения (103), то общее
решение соответствующего неоднородного
уравнения (102) может быть найдено по
формуле
![]()
где функции ![]() и
и ![]() определяются из системы линейных
алгебраических уравнений
определяются из системы линейных
алгебраических уравнений
![]()
Интегрируя, находим
функции ![]() и
и ![]() и записываем общее решение неоднородного
уравнения.
и записываем общее решение неоднородного
уравнения.
3. используя начальные условия (102’), находим решение задачи Коши.
Записываем ответ
в виде ![]() .
.
Пример 31. Найти решение задачи Коши
![]()
с начальными
условиями ![]() .
.
Решение.
1. Записываем соответствующее однородное уравнение:
![]()
Находим фундаментальную
систему решений ![]() и
и ![]() и общее решение однородного уравнения
и общее решение однородного уравнения
![]()
2. применяем метод Лагранжа (метод вариации произвольных постоянных):
а) ищем решение данного неоднородного уравнения в виде
![]()
б) записываем систему уравнений для определения функций :
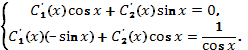
Решая ее (так как
решение ищем в окрестности точки ![]() ,
то
,
то ![]() ),
получим
),
получим
![]()
Интегрируя, находим
![]()
в) записываем полученное общее решение данного неоднородного уравнения
![]()
3. используя
начальные условия, определяем константы
![]() и
и ![]() .
.
Так как
![]()
то ![]() .
Так как
.
Так как
![]()
то ![]() .
.
Ответ. ![]() ю
ю
Условия задач. Найти решения задач Коши для дифференциальных уравнений.
1. ![]() Ответ:
Ответ: ![]()
2.![]() Ответ:
Ответ:![]() .
.
