12.15. Понятие решения
Постановка
задачи.
Доказать, что функция 
удовлетворяет дифференциальному
уравнению 
.
Алгоритм решения.
Для доказательства
того, что функция 
удовлетворяет уравнению 
,
достаточно вычислить производную 
,
подставить 
и 
в это уравнение и убедиться в том, что
получается тождество, т.е. 
для всех допустимых х.
Пример 21.
Доказать, что функция 
удовлетворяет уравнению 
.
Решение. Имеем
.
Подставим 
и 
в левую часть уравнения и проведем
необходимые преобразования:
Получаем тождество
.
Ответ. Функция 
удовлетворяет заданному уравнению.
Условия задач.
Доказать, что функция 
удовлетворяет дифференциальному
уравнению 
.
1. 
.
.
.
12.16. Уравнения с разделяющимися коэффициентами
Постановка задачи. Найти интегральные кривые дифференциального уравнения вида
Алгоритм решения.
1. В области, где
и 
разделяем переменные, т.е. представляем
уравнение (67) в виде
2. Вычислим интегралы в уравнении
и преобразуем его
к виду 
.
3. Ответ записываем
в таком виде: интегральные кривые
определяются уравнением 
при всех возможных значениях С.
Замечание 11.
Если одно или оба уравнения 
и 
имеют решения 
и 
, то равенства 
и 
нужно присоединить к ответу, так как
они являются интегральными кривыми
дифференциального уравнения (67).
Пример 22. Найти интегральные кривые дифференциального уравнения
Решение.
1. Перепишем исходное
уравнение в виде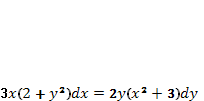 
.
(68)
Поскольку 
и 
,
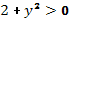разделяем переменные, т.е. представляем
уравнение (68) в виде
2. Вычислим интегралы в уравнении
Имеем
Следовательно, ,
где 
.
3. Упростив это
равенство, получим 
.
Ответ. Интегральные кривые определяются уравнением
при всевозможных значениях С.
Условия задач. Найти интегральные кривые дифференциальных уравнений.
1. 
.
Ответ: 
2. 
Ответ: 
12.17. Однородные уравнения
Постановка задачи. Найти интегральные кривые однородного дифференциального уравнения первого порядка, т.е. дифференциального уравнения вида
где 
и 
- однородные функции одинакового порядка,
т.е. 
и 
.
Алгоритм решения.
1. Преобразуем
уравнение (69) к виду 
2. Делаем подстановку
,
где 
- новая неизвестная функция. Тогда 
и уравнение
(69’)
приводится к виду
т.е. к уравнению с разделяющимися переменными.
Заметим, что
подстановку 
можно делать сразу в уравнении (69), не
приводя его к виду (69’).
3. Разделяем
переменные в области, где 
:
4. Интегрируем
полученное уравнение с разделенными
переменными и делаем замену 
.
Записываем ответ.
Замечание 12.
Если 
- корень уравнения 
,
то решением уравнения (69) будет также
.
Замечание 13. Интегральные кривые однородного уравнения можно искать и в полярных координатах.
Пример 23. Найти интегральные кривые дифференциального уравнения
Решение.
1. Преобразуем заданное уравнение к виду
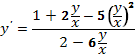
(мы разделили
числитель и знаменатель правой части
заданного уравнения на 
).
2. Делаем подстановку
,
где 
– новая неизвестная функция. Тогда 
и уравнение
приводится к виду
т.е. к уравнению с разделяющимися переменными.
В результате простых преобразований получаем
3. Разделяем
переменные 
:
4. Интегрируя, получаем
Заменяя 
на 
,
получаем
Ответ. Интегральные кривые определяются уравнением
при всех возможных значениях С.
Условия задач. Найти интегральные кривые дифференциальных уравнений.
1. 
Ответ: 
2. 
Ответ: 