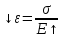- •Раздел II Сопротивление материалов
- •Тема 2.1. Основные положения. Гипотезы и допущения
- •Основные требования к деталям и конструкциям и виды расчетов в сопротивлении материалов Механические свойства материалов
- •Виды расчетов
- •Основные гипотезы и допущения
- •Допущения о свойствах материалов
- •Допущения о характере деформации
- •Классификация нагрузок и элементов конструкции
- •Формы элементов конструкции
- •Нагрузки внешние и внутренние, метод сечений
- •Метод сечений
- •Напряжения
- •Тема 2.2. Растяжение и сжатие.
- •Внутренние силовые факторы, напряжения.
- •Построение эпюр
- •Растяжение и сжатие
- •Примеры построения эпюры продольных сил
- •Напряжения при растяжении и сжатии
- •Деформации при растяжении и сжатии
- •Закон Гука
- •Формулы для расчета перемещений поперечных сечений бруса при растяжении и сжатии
- •Механические испытания. Статические испытания на растяжение и сжатие
- •Предельные и допустимые напряжения
- •Тема 2.3 практические расчеты на срез и смятие
- •Тема 2.4.Геометрические характеристики сечений Полярный и осевые моменты инерции
- •Тема 2.5 кручение
- •Напряжения и деформации при кручении вала
- •Расчеты на прочность и жесткость при кручении
- •Тема 2.7 Понятие о гипотезах прочности.
Напряжения при растяжении и сжатии
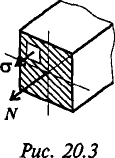
При растяжении и сжатии в сечении действует только нормальное напряжение.
Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.
Таким
образом, направление
и знак напряжения в
сечении совпадают
с направлением и знаком силы в сечении
.
Исходя
из гипотезы плоских сечений, можно
предположить,
что напряжения при растяжении и сжатии
в пределах каждого сечения не меняются.
Поэтому
напряжение можно рассчитать по формуле
![]()
где Nz — продольная сила в сечении;
А — площадь поперечного сечения.
Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
Нормальные напряжения действуют при растяжении от сечения, а при сжатии к сечению.
Размерность (единица измерения) напряжений — Н/м2 (Па), однако это слишком малая единица, и практически напряжения рассчитывают в Н/мм2 (МПа): 1 МПа = 106Па = 1 Н/мм2.
При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений.
Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.
Строится
и оформляется такая эпюра так же, как и
эпюра продольных
сил.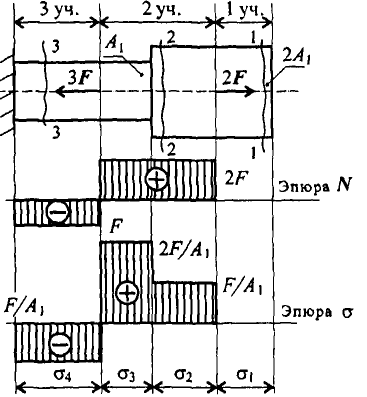
Рассмотрим брус, нагруженный внешними силами вдоль оси .
Обнаруживаем три участка нагружения и определяем величины продольных сил.
Участок 1: Л/1 = 0. Внутренние продольные силы равны нулю.
Участок 2: ЛГ2 = 2Р. Продольная сила на участке положительна.
Участок 3: ЛГ3 = 2Р-—ЗР = —Р. Продольная сила на участке отрицательна.
Брус — ступенчатый.
С учетом изменений величин площади поперечного сечения участков напряжений больше.
![]()
Строим эпюры продольных сил и нормальных напряжений. Масштабы эпюр могут быть разными и выбираются исходя из удобства построения.
Деформации при растяжении и сжатии
Рассмотрим деформацию бруса под действием продольной силы F.
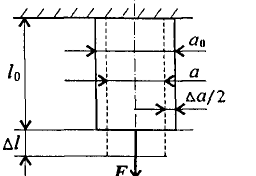
Начальные размеры бруса: lо — начальная длина, ао — начальная ширина.
Брус удлиняется на величину ∆l;
∆l - абсолютное удлинение.
При растяжении поперечные размеры уменьшаются, ∆а — абсолютное сужение;
∆l > 0; ∆а <0.
При сжатии выполняется соотношение
∆l < 0; ∆а > 0.
В сопротивлении материалов принято рассчитывать деформации в относительных единицах:
ε = ∆l/ lо; ε — относительное удлинение;
ε' = ∆а/ ао; ε' — относительное сужение.
Между продольной и поперечной деформациями существует зависимость
ε' = με,
где μ — коэффициент поперечной деформации, или коэффициент Пуассона, характеристика пластичности материала.
Закон Гука
В пределах упругих деформаций деформации прямо пропорциональны нагрузке: F=k ∆l
где F — действующая нагрузка; k — коэффициент.
В современной форме: σ =N/A; ε = ∆l/ lо;
Получим зависимость σ= Еε, где Е — модуль упругости, характеризует жесткость материала.
В пределах упругости нормальные напряжения пропорциональны относительному удлинению.
Значение Е для сталей в пределах (2…2,1) • 105 МПа.
При
прочих равных условиях, чем жестче
материал, тем меньше он деформируется: