Основные характеристики выборки

Числовые характеристики X:

1. M*(x) = 5,4433;

2. D*(x) = 7,4088;

3. S²(x) = 7,4836;

4. σ*(x) = 2,7219;

5. s*(x) = 2,7365;

6. 

7. 

8. 

9. 

10. 

11. 

12. начальные и центральные моменты первого, второго и третьего порядков:

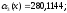
Числовые характеристики Y:

1. M*(y) = 10,6568;

2. D*(y) =39,6181;

3. S²(y) =40,0182;

4. σ*(y) = 6,2943;

5. s*(y) = 6,3260;

6. 

7. 

8. 

9. 

10. 

11. 

12. начальные и центральные моменты первого, второго и третьего порядков:

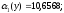
Корреляционный момент и коэффициент корреляции :

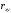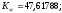
Полученное значение коэффициента корреляции характеризует обратную связь между исследуемыми величинами, т. к. оно положительно. Так как принимает значение близкое к 1, то X и Y зависимы. При увеличении X Y увеличивается.

Построим диаграмму рассеивания для данных значений X и Y:

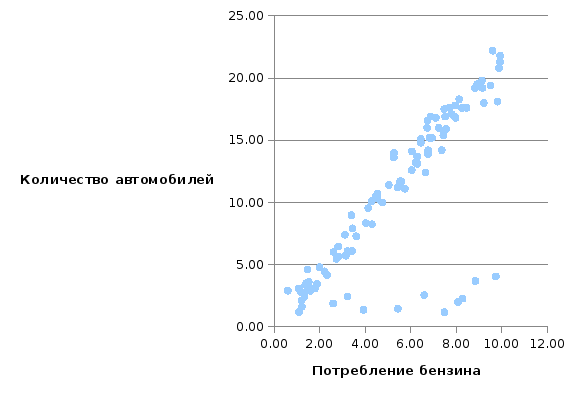
Рис. 1. Диаграмма рассеивания

Корреляционный анализ

Для корреляционного анализа данные удобнее представить в виде корреляционной таблицы. Область попадания точек разбиваем на 7 интервалов по X и 7 по Y. В первой строке таблицы укажем средние значения интервалов для Y, а в первом столбце – средние значения интервалов по X. На пересечении строк и столбцов находятся частоты наблюдаемых пар значений признаков.

x/y	1,4286	2,8572	4,2857	5,7143	7,1429	8,5714	10	ny
3,2857	8	4	2	1	1	3	0	19
6,5715	2	10	3	0	0	0	2	17
9,8572	0	0	6	1	0	0	0	7
13,1429	0	0	1	10	4	0	0	15
16,4286	0	0	0	2	10	5	0	17
19,7143	0	0	0	0	3	10	6	19
23	0	0	0	0	0	0	6	6
nx	10	14	12	14	18	18	14	100

С помощью корреляционной таблицы мы сможем найти оценки для X:

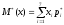, где , = 6,0857;

, =7,4946;

, = 8,7473;

, =2,7376;

, =2,9570.

С помощью корреляционной таблицы найдем числовые характеристики Y:

, где , =12,3215;

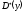, =41,7532;

, =48,7121;

, = 6,4617;

, =6,9794.

Вычислим начальные моменты первого, второго и третьего порядков для X и Y:

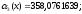
Вычислим центральные моменты второго и третьего порядков для X и Y:

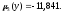
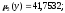
Используя данные корреляционной таблицы, построим гистограммы, полигоны и графики эмпирических функций распределения для X и Y (см. рис. 2 — рис. 7):

Рис. 2. Гистограмма частот по X

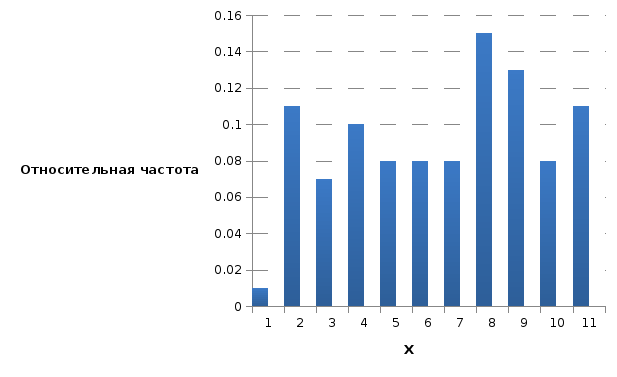
Рис. 3. Гистограмма относительных частот по X

Рис. 4. Гистограмма частот по Y

Рис. 5. Гистограмма относительных частот по Y

Гистограмма представляет собой графическое изображение зависимости частоты попадания элементов выборки от соответствующего интервала группировки.

Рис. 6. Полигон частот по X

Рис. 7. Полигон относительных частот по X

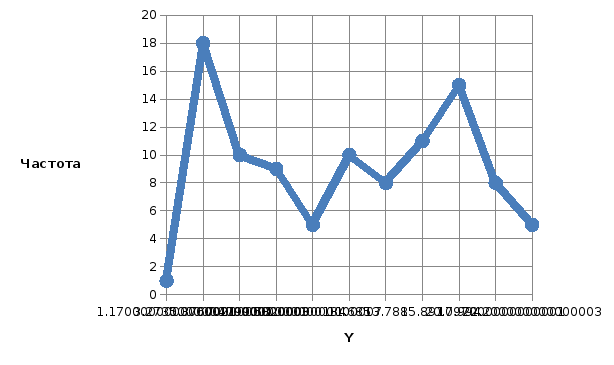
Рис. 8. Полигон частот по Y

Рис. 9. Полигон относительных частот по Y

Полигоны представляют собой один из способов графического представления плотности вероятности случайной величины.

Рис. 10. Эмпирическая функция распределения по X

Рис. 11. Эмпирическая функция распределения по Y

Эмпирическая функция распределения служит для оценки теоретической функции распределения генеральной совокупности.