
- •§ 1. Схема расчета нетто-премий
- •§ 2. Полное страхование жизни
- •2.1. Полное дискретное страхование жизни
- •2.2. Полное непрерывное страхование жизни
- •2.3. Полное непрерывное страхование жизни с выплатой премий т раз в год
- •§ 3. Временное страхование жизни
- •§ 4. Страхование рент
- •§ 5. Расчет защитной надбавки
- •5.1.Вероятность неразорения
- •5.2. Полное страхование жизни
- •§ 6. Актуарное накопление для страховых рент
- •§ 7. Премии, учитывающие издержки
§ 4. Страхование рент
Наиболее общая схема страхования жизни определяется последовательностью страховых выплат произвольной величины, осуществляемой страховой компанией в произвольные моменты времени, и соответствующей произвольной последовательностью страховых взносов застрахованного. Чтобы определить величину страховых взносов необходимо снова воспользоваться условием (1) финансовой эквивалентности обязательств застрахованного и страховой компании.
Рассмотрим, для определенности, вид страхования жизни, называемый страхованием рент, который применяется , например, при накопительных схемах пенсионного страхования.
При
этом виде страхования застрахованный
в возрасте x
лет осуществляет периодические взносы
страховой компании в течение n
лет. Страховая компания регулярно
(периодически) выплачивает страховые
суммы (по достижении застрахованным
возраста
![]() лет) или в течение некоторого конечного
периода, или пожизненно.
лет) или в течение некоторого конечного
периода, или пожизненно.
Предположим
сначала, что выжидательный период
![]() лет отсутствует, и выплаты производятся
пожизненно. Тогда актуарная стоимость
обязательств застрахованного будет
равна:
лет отсутствует, и выплаты производятся
пожизненно. Тогда актуарная стоимость
обязательств застрахованного будет
равна:
![]()
а актуарная стоимость обязательств компании, по ежегодной выплате единичной суммы, будет равна актуарной стоимости отсроченной пожизненной ренты:
![]()
Следовательно,
![]()
то есть периодическая нетто-премия будет вычисляться по формуле:
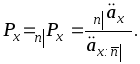 (11)
(11)
Если период уплаты взносов n меньше срока отсрочки m, то величина ежегодного взноса определяется как
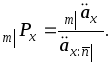 (11ґ)
(11ґ)
Если договором страхования предусматриваются не пожизненные страховые выплаты, а речь идет о k – летней ренте, то формула (11ґ) примет вид
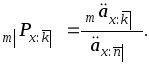 (12)
(12)
№ 43. Вычислите нетто-премию при страховании пожизненной ренты, если страховые взносы вносятся застрахованным в течение 5 лет. Выжидательный период отсутствует, возраст застрахованного - 30 лет, годовая процентная ставка равна 20%.
Решение. Применим формулу (11):
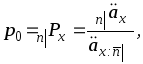
где
![]()
Вычислим
параметры, входящие в эту формулу. Начнем
с
![]() :
:
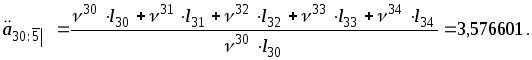
Для
вычисления
![]() воспользуемся формулой (13) гл. 4:
воспользуемся формулой (13) гл. 4:
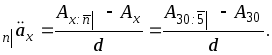
где
![]()
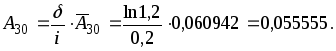
Следовательно,
![]()
и искомая нетто-премия будет равна:
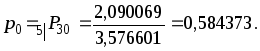
Ответ: 0,584373.
Аналогичным образом можно рассмотреть вопрос о страховании рент в случае, когда как премии, так и страховые выплаты, осуществляются несколько раз в год.
Здесь мы рассмотрели лишь некоторые варианты договоров страхования и пенсионных схем. Исходя из принципа финансовой эквивалентности (1) можно проанализировать и более широкий круг договоров страхования.
§ 5. Расчет защитной надбавки
5.1.Вероятность неразорения
Известно,
что для защиты от случайных вариаций
продолжительности жизни нетто-премия
![]() должна быть дополнена соответствующей
защитной надбавкой
должна быть дополнена соответствующей
защитной надбавкой
![]() ,
то есть полная нетто-премия будет равна
,
то есть полная нетто-премия будет равна
![]() ,
(13)
,
(13)
где
![]() - относительная страховая надбавка.
- относительная страховая надбавка.
Введем в рассмотрение
случайную величину
![]() - современную стоимость убытка, связанного
с одним договором страхования
- современную стоимость убытка, связанного
с одним договором страхования
![]() ,
(14)
,
(14)
где
![]() и
и
![]() - современные (не актуарные) стоимости
обязательств страховой компании и
застрахованного. Тогда компания, имеющая
портфель из
- современные (не актуарные) стоимости
обязательств страховой компании и
застрахованного. Тогда компания, имеющая
портфель из
![]() договоров страхования с убытками
договоров страхования с убытками
![]() ,
,
![]() не разорится, если суммарный убыток
не разорится, если суммарный убыток
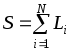 будет неположительным, то есть
будет неположительным, то есть
![]() .
.
Если
принять за
![]() вероятность неразорения компании, то
получим
вероятность неразорения компании, то
получим
![]() ,
(15)
,
(15)
или
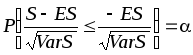 .
.
В случае нормального приближения можем написать
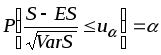 ,
(15ґ)
,
(15ґ)
где
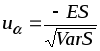 -
(16)
-
(16)
квантиль нормального распределения.
Решив
уравнение (16) относительно неизвестной
![]() ,
можем найти как полную премию
(брутто-премию)
,
можем найти как полную премию
(брутто-премию)
![]() ,
так и относительную страховую надбавку
,
так и относительную страховую надбавку
Рассмотрим некоторые виды страхования жизни с периодическими брутто-премиями.
