Г Л А В А V
П Е Р И О Д И Ч Е С К И Е П Р Е М И И
§ 1. Схема расчета нетто-премий
В
предыдущих главах мы рассмотрели
долгосрочные контракты по страхованию
жизни, которые оплачивались единовременным
страховым взносом
(премией)
.
Однако такие контракты встречаются
достаточно редко, так как слишком велика
их стоимость. Как правило, долгосрочные
страховые контракты оплачиваются
застрахованным в рассрочку (периодически)
– ежегодно, ежеквартально, ежемесячно.
Предположим, что страховая премия выплачивается в виде серии платежей в течение некоторого срока с момента заключения договора страхования. При такой периодической уплате взносов застрахованный выполняет свои обязательства в рассрочку. Однако при этом стоимость обязательств компании не зависит от способа уплаты страховых премий.
При расчете величины периодически уплачиваемых премий необходимо учитывать как процентный доход от инвестиций, так и демографические факторы (смертность). Последний фактор оказывает существенное влияние на величину взносов, так как не все застрахованные успевают уплатить все предусмотренные контрактом взносы.
В
общем виде, схема
расчета нетто-премий
может быть представлена следующим
образом. Пусть
- искомая нетто-премия. Тогда современная
актуарная стоимость обязательств
застрахованного
будет функцией
,
то есть
.
Актуарная современная стоимость
финансовых обязательств компании
также является функцией
:
.
И для вычисления
необходимо применить принцип финансовой
эквивалентности обязательств страховой
компании и застрахованного, а это
означает, что необходимо решить уравнение:
,
(1)
которое представляет собой условие равенства обязательств застрахованного и страховой компании на момент заключения договора страхования.
Отметим,
что, как и ранее, полная периодическая
премия состоит из нескольких частей:
периодическая нетто-премия
,
защитная (страховая) надбавка
и расходы, возмещающие организационные
затраты.
Применим теперь общую схему (1) к различным вариантам страхования жизни.
§ 2. Полное страхование жизни
2.1. Полное дискретное страхование жизни
Пусть
плата за страховку вносится в начале
каждого года с момента заключения
договора страхования в сумме
в течение всей жизни. Так как договор
страхования вступает в силу только
после получения компанией первого
взноса, то рента страховых платежей
(премий) является рентой пренумерандо.
Тогда актуарная приведенная стоимость
потока премий на момент заключения
договора страхования будет равна:
.
Страховая
компания выплачивает единичную сумму
в конце года смерти
застрахованного. Актуарная современная
стоимость этой суммы на момент заключения
договора страхования будет равна
,
то есть
.
Следовательно, из равенства (1) получаем:
,
или
.
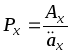(2)
Формула
(2) показывает во сколько раз величина
ежегодного взноса
меньше величины единовременно
уплачиваемого взноса
.
Поэтому величину коэффициента приведения
годовой ренты
называют еще коэффициентом
рассрочки.
Периодическую
нетто-премию
можно выразить и при помощи характеристик,
рассмотренных нами ранее, как:
,
,
.
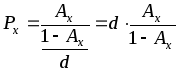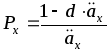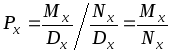(2ґ)
№ 38. Вычислите периодическую нетто-премию при полном дискретном страховании жизни человека в возрасте 30 лет, если эффективная годовая процентная ставка равна 20%, а продолжительность жизни описывается моделью де Муавра с предельным возрастом в 120 лет. Обязательства страховой компании заключаются в выплате 100000 руб. в конце года смерти застрахованного.
Решение. Учитывая результаты, полученные в №№ 29 и 32, можем вычислить:
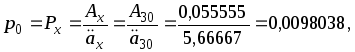
или в рублях:
руб.
Таким образом, ежегодный платеж при полном дискретном страховании жизни составит 980,38 руб.
Ответ: 980,38 руб.
Если период уплаты нетто-премий ограничен, например, n годами, то обязательства застрахованного будут выглядеть как
,
и ежегодная нетто-премия будет равна:
.
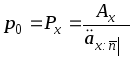(3)