2. Описание экспериментальной установки
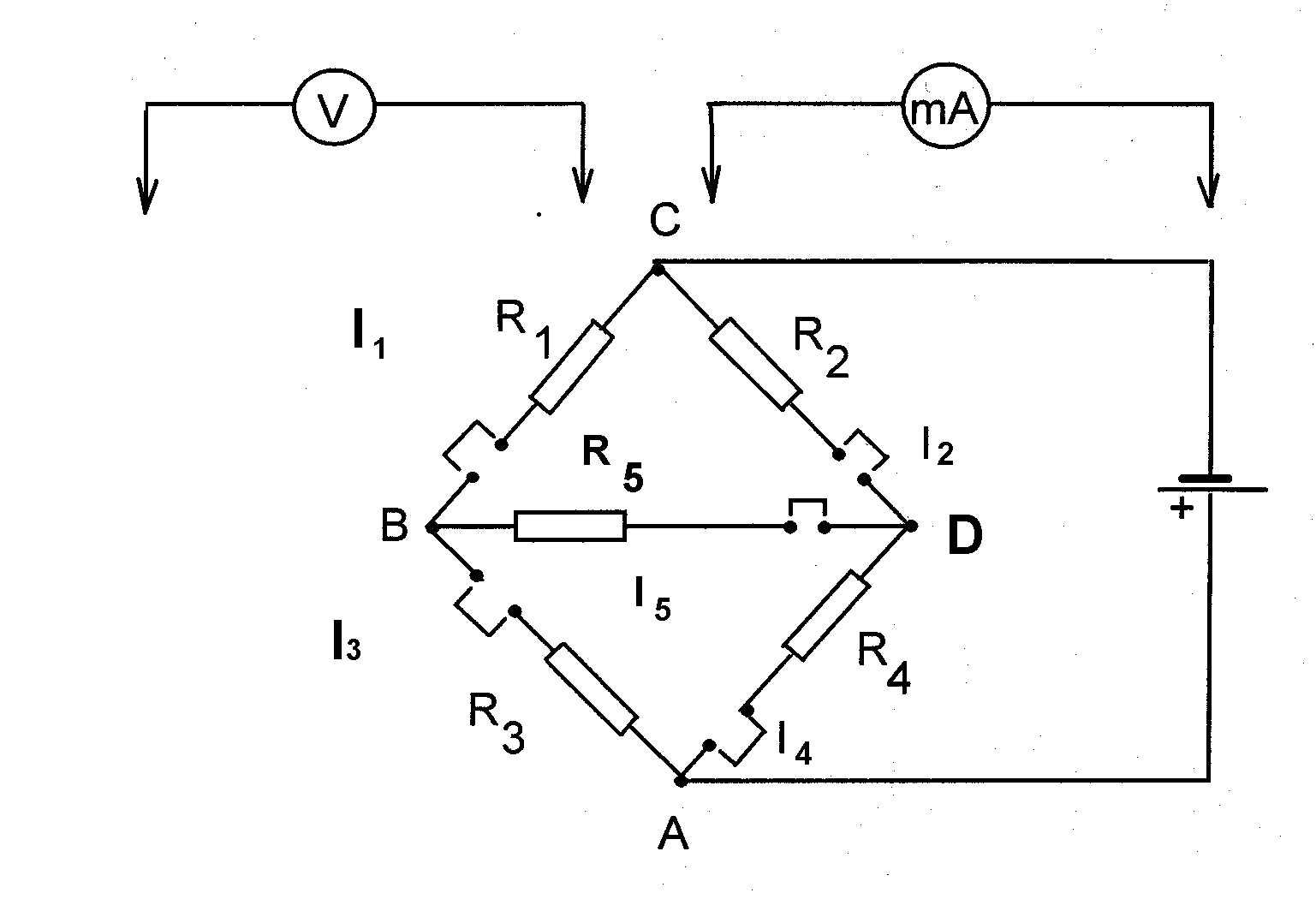
Рис.5.2. Схема экспериментальной установки
Схема установки для выполнения работы изображена на рис. 5.2 . Она состоит из макета, источника питания, вольтметра и амперметра. Номиналы резисторов R1-R5 определяются по маркировке на каждом резисторе. Буква R в номинале обозначает основную единицу измерения - Ом, другие буквы - это сокращенные обозначения десятичных приставок: к - кило, м -мега, г - гига. Если число стоит перед буквой, то оно обозначает целое число единиц указанного буквой разряда, если число стоит после буквы, то оно обозначает дробные доли указанного разряда. Например: 24к - 24 кОм, м12 - 0,12 МОм, 1к6 - 1,6 кОм.
3. Порядок выполнения работы
1. Нарисовать схему макета с указанием номиналов резисторов, входящих в схему.
2. Подключить общее напряжение на схему U6 = 10 В.
3. При помощи вольтметра, измерить падение напряжения на всех резисторах схемы. Результаты измерений занести в таблицу:
|
|
U1 |
U2 |
U3 |
U4 |
U5 |
U6 |
I1 |
I2 |
I3 |
I4 |
I5 |
I6 |
|
измеренные значения |
|
|
|
|
|
|
|
|
|
|
|
|
|
расчетные значения |
|
|
|
|
|
|
|
|
|
|
|
|
4. Измерить токи во всех ветвях цепи. Для этого нужно вынуть соответствующую перемычку и вставить вместо нее контакты миллиамперметра.
5. На основании уравнений Кирхгофа по известным сопротивлениям рассчитать токи и падения напряжений.
6. Сравнить расчетные данные с экспериментально измеренными.
7. Оцените экспериментальные ошибки. Объяснить возможные причины расхождений.
Контрольные вопросы
1. Сформулируйте и поясните закон Ома для полной цепи.
2. Сформулируйте правила Кирхгофа. К каким цепям они применяются?
3. Будут ли справедливы правила Кирхгофа для цепи, включающей в себя полупроводниковые диоды?
Литература
1. Савельев И.В. Курс общей физики. Т.2, М.: Наука, 1987.
2. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. 8-е изд. М.: Высшая школа, 1984.
Лабораторная работа №6
ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель работы: экспериментальное исследование электростатического поля в области между заряженными электродами различной конфигурации и описание его при помощи эквипотенциальных поверхностей и силовых линий.
Приборы и принадлежности: стенд ЮУрГУ, соединительные провода.
1. Краткая теория
1.1. Электростатическое поле. Напряженность поля
Электростатическое поле представляет собой частный случай электромагнитного поля и создается неподвижными электрическими зарядами. Электростатическое поле в каждой точке характеризуется значениями напряженности Е и потенциала φ, которые являются силовой и энергетической характеристиками поля в данной точке.
Дейсвие элекиростатического поля проявляется в том, что помещенный в какую-либо точку пространства пробный заряд q оказывается под действием некоторой силы F со стороны поля. За напряженность поля E принимается векторная величина, по определению равная:
E
= F/q
,
(6.1)
и характеризующая электрическое поле в данной точке. Согласно формуле (1) напряженность электрического поля численно равна отношению силы, действующей на помещенный в данную точку поля точечный заряд, к величине этого заряда, а направление вектора E совпадает с направлением силы, действующей на положительный заряд.
Напряженность поля, созданного точечным зарядом q в вакууме, как следует из закона Кулона, в системе "СИ" определяется формулой:
, (6.2)
где ε0 - электрическая постоянная, равная 8,85·10-12 Ф/м, r - расстояние от заряда до данной точки, r/çrï - единичный вектор, направленный от заряда к данной точке.
Для электрического поля справедлив принцип суперпозиции:
E = SEi , (6.3)
где E - напряженность поля системы зарядов, Ei - напряженность поля, создаваемого отдельным зарядом.
Таким образом, электрическое поле можно описать, указав для каждой точки пространства величину и направление вектора напряженности E. Совокупность этих векторов образует некоторое векторное поле. Силовые линии или линии вектора напряженности проводят так, что касательные к ним в каждой точке совпадают с направлением вектора E в этой точке, а количество линий, пронизывающих единицу поверхности перпендикулярной направлению вектора E численно равно значению E.