
- •010400.62 «Прикладная математика и информатика»
- •Введение
- •§1. Классификация интегральных уравнений
- •§2. Задачи, приводящие к интегральным уравнениям Вольтерра
- •Задача o таутохроне
- •Задачи Коши для дифференциальных уравнений первого порядка
- •3.Задача Коши для линейных уравнений высших порядков
- •4.Краевые задачи для дифференциальных уравнений
- •§3 Интегральные уравнения Вольтера как частный случай уравнений Фредгольма
- •§4. Решение интегральных уравнений Вольтерра методом дифференцирования
- •§5. Решение интегральных уравнений с помощью степенных рядов
- •§6. Решение интегральных уравнений Вольтерра методом последовательных приближений
- •Уравнение второго рода
- •Уравнения первого рода
- •§7. Интегральные уравнения Вольтерра с вырожденными ядрами
- •Уравнения Вольтерра второго рода
- •Уравнения Вольтерра первого рода
- •§8. Решение уравнений Вольтерра второго рода с помощью ряда Неймана
- •§9. Итерированные ядра и резольвента интегральных уравнений Вольтерра
- •!!!§10. Решение уравнений Вольтерра с разностными ядрами с помощью преобразования Лапласа
- •§11. Задачи для самостоятельного решения
- •Литература
- •Содержание
§9. Итерированные ядра и резольвента интегральных уравнений Вольтерра
В
полученных выражениях (8.3) коэффициентов
ряда Неймана
![]() последовательно произведем подстановку
последовательно произведем подстановку
![]() в
в![]() ,
затем
,
затем
![]() в
в
![]() и так далее, сменив обозначения переменных
и так далее, сменив обозначения переменных
 .
.
 .
.
В кратных интегралах изменим порядок интегрирования в соответствии с ниже изображенной областью интегрирования
S
S=t
x








а




0
t
x
а
 .
.
Как и для интегральных уравнений Фредгольма, приняв за первое итерированное ядро данное ядро, за второе итерированное ядро примем

тогда
 .
.
Аналогично найдем
![]()

где

………………………………………………………………………..
 (9.1)
(9.1)
где
 (9.2)
(9.2)
…………………………………… .
Подставим
полученные выражения коэффициентов
![]() ,
в соответствии с полученными формулами
(9.1), в ряд (8.2) и, в силу равномерной и
абсолютной сходимости этого ряда, можем
просуммировать интегралы
,
в соответствии с полученными формулами
(9.1), в ряд (8.2) и, в силу равномерной и
абсолютной сходимости этого ряда, можем
просуммировать интегралы
![]()
Выражение в квадратных скобках назовем резольвентой интегрального уравнения Вольтерра второго рода и для нее введем обозначение
![]() (9.3)
(9.3)
Если итерированные ядра найдены, а следовательно и резольвента, то решение интегрального уравнения Вольтерра (8.1) определится по формуле
 .
(9.4)
.
(9.4)
Аналогично,
группируя интегралы попарно в формулах
(9.1) для коэффициентов
![]() начиная с последней пары, для итерированных
ядер получим другую формулу
начиная с последней пары, для итерированных
ядер получим другую формулу
 n=2,3,…
. (9.5)
n=2,3,…
. (9.5)
В формулу резольвенты (9.3) подставив выражения итерированных ядер (9.2)

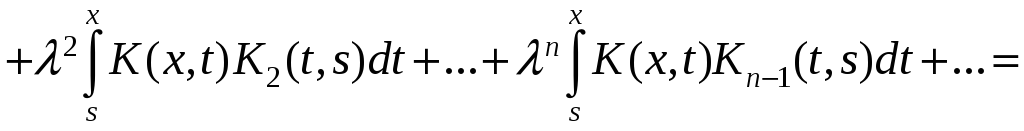
![]()

получим интегральное уравнение резольвенты
 (9.6)
(9.6)
Если в формулу резольвенты (9.3) подставить выражения итерированных ядер (9.5), то получим другое интегральное уравнение резольвенты
 .
(9.7)
.
(9.7)
Пример 10. Построить резольвенту ядра K(x,t) = x – t .
Решение. По формулам (9.2) находим итерированные ядра
![]()
![]()
![]() …………..,
…………..,
и по индукции выписываем
![]() ………….
.
………….
.
Затем по формуле (9.3) находим резольвенту
![]()
Пример 11. Вычислив итерирование ядра и резольвенту, найти решение уравнения
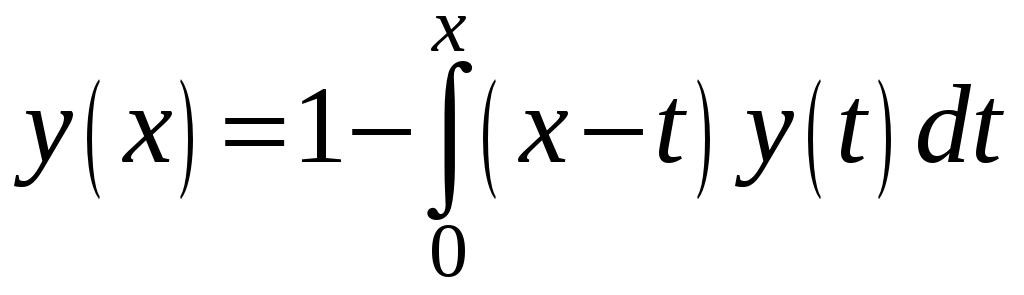 .
.
Решение.
Положив
![]() ,
выпишем ядро
,
выпишем ядро
![]() .
.
Далее по формулам (9.2) найдём

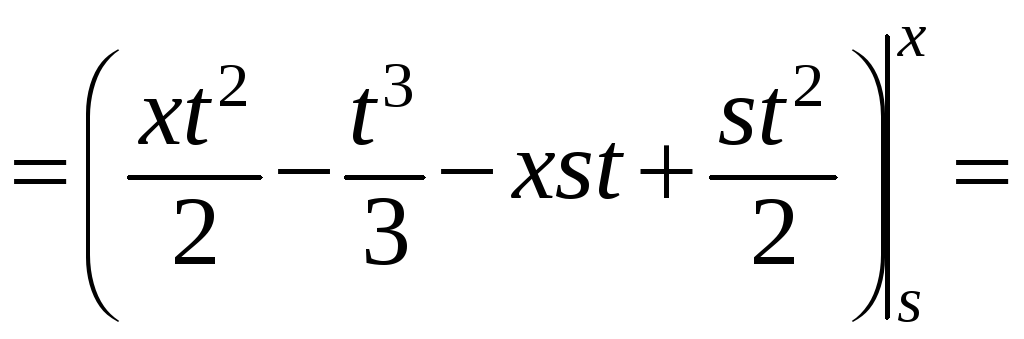
![]() ,
,
![]()
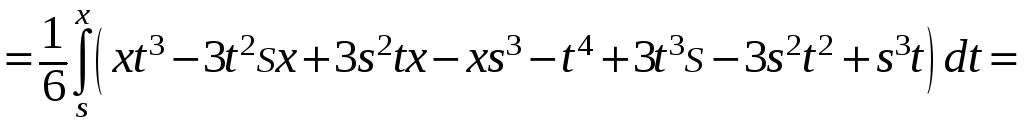

 ,
,
…………………………………………………………………….. .
По индукции выпишем n-ое итерированное ядро
![]()
и по формуле (9.3 ) найдём резольвенту
 .
.
Решение интегрального уравнения получим по формуле (9.4)

Ответ:
![]()
Нетрудно проверить что найденная функция является решением исходного уравнения

!!!§10. Решение уравнений Вольтерра с разностными ядрами с помощью преобразования Лапласа
Преобразование
Лапласа
для произвольной (комплекснозначной)
функции ![]() действительного переменного
действительного переменного ![]() определяется следующим образом:
определяется следующим образом:
 (10.1)
(10.1)
где
![]() – комплексная переменная.
– комплексная переменная.
Функция
![]() называется оригиналом, а
называется оригиналом, а ![]() –изображением
(образом) функции
–изображением
(образом) функции ![]() .
.
Преобразование
Лапласа существует для непрерывных и
кусочно-непрерывных функций, удовлетворяющих
условию ![]() ,
где
,
где ![]() - некоторые
числа. Далее считаем, что в указанной
оценке взято наименьшее из возможных
чисел
- некоторые
числа. Далее считаем, что в указанной
оценке взято наименьшее из возможных
чисел ![]() ,
которое называется
показателем
роста
функции
f(x).
,
которое называется
показателем
роста
функции
f(x).
Для всякого
оригинала f(x)
функция
![]() определена в полуплоскости
определена в полуплоскости ![]() и является в этой полуплоскости
аналитической функцией.
и является в этой полуплоскости
аналитической функцией.
Формулу (10.1) кратко будем записывать так:
![]()
По
известному изображению ![]() оригинал находится с помощью обратного
преобразования Лапласа
оригинал находится с помощью обратного
преобразования Лапласа
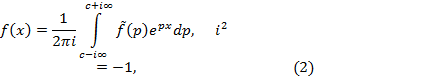 (10.2)
(10.2)
где путь интегрирования
расположен параллельно мнимой оси
комплексной плоскости справа от всех
особых точек функции f(p),что
соответствует ![]() .
.
Интеграл в (10.2) понимается в смысле главного значения

Формула
(10.2) справедлива для непрерывных функций.
В отрицательной области формула (10.2)
даёт ![]() .
.
Если в точке ![]() ,
функция
f(x)имеет
конечный разрыв первого рода, то правая
часть формулы (10.2) в этой точке дает
значение
,
функция
f(x)имеет
конечный разрыв первого рода, то правая
часть формулы (10.2) в этой точке дает
значение ![]() (при
(при ![]() первый член в квадратных скобках должен
быть опущен).!!!
первый член в квадратных скобках должен
быть опущен).!!!
Формулу обращения преобразования Лапласа (10.2) кратко будем записывать так:
![]()
Сверткой
(по Лапласу)
двух функций f(x)
и
![]() называется выражение
называется выражение
![]() !!!
!!!
Справедлива теорема о свертке:
![]()
которая часто используется при решении уравнений Вольтерра с разностным ядром [2]. [20], [33].
Уравнения Вольтерра второго рода с ядром, зависящим от разности аргументов, имеют вид
![]() (10.3)
(10.3)
Применяя
преобразование Лапласа £ к уравнению
(10.3) и учитывая, что интеграл с ядром,
зависящим от разности аргументов, по
теореме о свертке преобразуется в
произведение ![]() приходим к уравнению для образа искомой
величины
приходим к уравнению для образа искомой
величины
![]() (10.4)
(10.4)
Решение уравнения (10.4) определяется формулой
![]() (10.5)
(10.5)
которую можно записать в эквивалентном виде
![]() (10.6)
(10.6)
Применяя к (10.6) обратное преобразование Лапласа, получим решение уравнения (10.3) в виде
(5)![]() (10.7)
(10.7)
где
![]()
При использовании формулы (10.7) могут возникнуть технические трудности:
1°. При получении
изображения ![]() для конкретного ядра
для конкретного ядра ![]()
2°. При нахождении
оригинала резольвенты (10.7), изображение
которого ![]() находится по формуле (10.6).
находится по формуле (10.6).
Для вычисления соответствующих интегралов применяют таблицы прямых и обратных преобразований Лапласа, причем во многих случаях для обратного преобразования используют методы теории функций комплексного переменного, включая теорему о вычетах.
Замечание.
Если нижний предел в интеграле уравнения
Вольтерра с ядром, зависящим от разности
аргументов, равен ![]() ,
то его можно свести к уравнению вида
(10.3) с помощью замены
,
то его можно свести к уравнению вида
(10.3) с помощью замены ![]()
Н а
рисунке приведена принципиальная схема
решения интегральных уравнений Вольтерра
второго рода с разностным ядром с помощью
интегрального преобразования Лапласа.
а
рисунке приведена принципиальная схема
решения интегральных уравнений Вольтерра
второго рода с разностным ядром с помощью
интегрального преобразования Лапласа.
Схема решения
интегральных уравнений Вольтерра
второго рода с разностным ядром с помощью
интегрального преобразования Лапласа,
![]() –оригинал
функции
–оригинал
функции
![]() .
.
Преобразование Лапласа можно применить для решения систем интегральных уравнений Вольтерра вида
![]()
Подействуем на систему преобразованием Лапласа. Тогда будем иметь
![]()
Решая эту
систему линейных алгебраических
уравнений, определим ![]() ,
и решение рассматриваемой системы
примет вид [2], [20]
,
и решение рассматриваемой системы
примет вид [2], [20]
![]()
Пример 12. Рассмотрим уравнение
![]()
которое
является частным случаем уравнения
(10.3) ![]()
Сначала, используя таблицы преобразований Лапласа, получим образ ядра интегрального уравнения в виде
![]()
Затем по формуле (10.6) найдем образ резольвенты
![]()
Используя далее таблицы обратных преобразований Лапласа, получим оригинал резольвенты

Заметим,
что в частном случае при ![]() получаем
получаем ![]() Подставляя эти выражения в формулу
(10.7), находим решение интегрального
уравнения. В частности, при
Подставляя эти выражения в формулу
(10.7), находим решение интегрального
уравнения. В частности, при ![]() это решение имеет вид [20]
это решение имеет вид [20]
![]()
Пример 13. Решить интегральное уравнение:
![]()
Решение. Известно, что
![]()
Пусть![]() .
Применяя преобразование Лапласа к обеим
частям уравнения и учитывая при этом
теорему умножения (изображения свертки),
получим
.
Применяя преобразование Лапласа к обеим
частям уравнения и учитывая при этом
теорему умножения (изображения свертки),
получим
![]()
Отсюда
![]()
или
![]()
Следовательно, решение данного интегрального уравнения есть
![]()
