-
Уравнения Вольтерра первого рода
(7.5)
где
условие 
,
будем считать выполненным.
Аналогично, как и в предыдущем случае вводим неизвестные функции
(7.6)
и дифференцируем это равенство
.
(7.7)
Затем дифференцируем исходное уравнение
откуда находим
.
(7.8)
Выразив
из соотношения (7.7) и подставив в (7.8),
получим систему линейных дифференциальных
уравнений для определения функций 
,
(7.9)
с
начальными условиями 
Если удастся найти решение системы (7.9) с этими начальными условиями, то решение определиться по формуле (7.7)
при
любом 
Значительно проще вопрос решается, если вырожденное ядро состоит из одного слагаемого
(7.11)
при
аналогичном условии 
.
Как и ранее вводим новую функцию
(7.12)
и дифференцируем ее
.
(7,13)
Затем дифференцируем исходное уравнение
и используя равенства (7.12) и (7.13) придем к линейному дифференциальному уравнению первого порядка
(7.14)
с
начальным условием 
.
Пример 8. Найти решение уравнения
Решение. Вводим новую функцию
и находим её производную
,
затем дифференцируем исходное уравнение и подставляем новую функцию в полученное уравнение
Поделив
результат на 
,
получим линейное дифференциальное
уравнение
и решаем его
Используя
начальное условие определяем значение
постоянной 
,
следовательно
и
.
Используя
это значение находим 
Ответ:
.
Нетрудно проверить что полученная функция удовлетворяет заданному уравнению, действительно, подставив найденное решение в исходное уравнение, найдём
=
§8. Решение уравнений Вольтерра второго рода с помощью ряда Неймана
Будем искать решение уравнения
(8.1)
в
виде ряда по степеням параметра
.
(8.2)
Подставив ряд (8.2) в уравнение (8.1)
и
приравнивая коэффициенты при одинаковых
степенях
слева и справа в полученном равенстве
(так как ряды слева и справа от равенства
равны только в этом случае) найдем
…,
…
(8.3)
Докажем сходимость ряда (8.2) при найденных выражениях его коэффициентов (8.3) при следующих ограничениях
(8.4)
в
квадрате 
.
Для выполнения условий (8.4) достаточно чтобы функция f(x) и ядро K(x,t) в рассматриваемой области были непрерывными. Для ядра K(x,t) можно условие ослабить, потребовав только его регулярность.Оценим коэффициенты ряда (8.2) по модулю в этой области
,
………………………………….…
,
……………………………… .
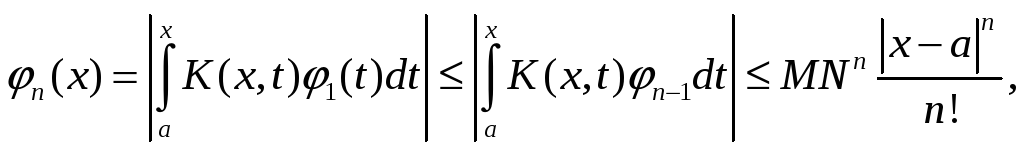
Построим ряд с полученными оценками коэффициентов ряда (8.2)
и
положив в нём
,
где
любое, получим числовой ряд
(8.5)
Числовой ряд (8.5) сходится по признаку Даламбера
.
Ряд (8.5) по построению является мажорирующим для ряда (8.2), следовательно ряд (8.2) по критерию Вейерштрасса сходится равномерно и абсолютно.
Пример 9. Решить уравнение
Решение. Найдём коэффициенты ряда (8.2)
.
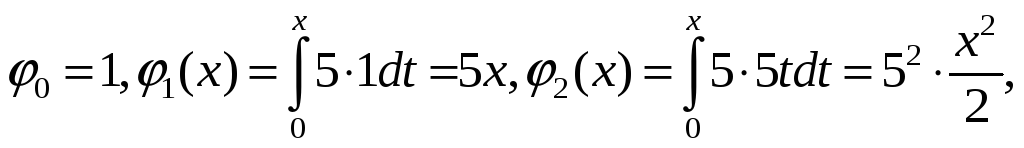
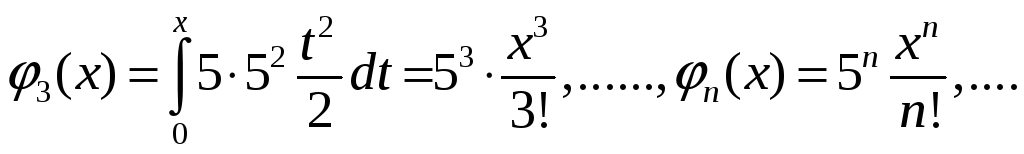Подставив
вычисленные коэффициенты в ряд (8.2) при
найдём
Ответ:
