§2. Задачи, приводящие к интегральным уравнениям Вольтерра

1. Задача o таутохроне

Найти кривую, скользя вдоль которой без трения тяжелая частица достигает своего самого низкого положения за одно и то же время независимо от её начального положения.

Решение. Выполним чертеж

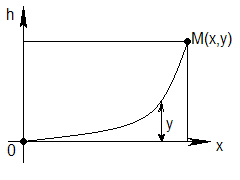
и введем обозначения , Т – постоянная величина, - функция от h, кривую будем искать в виде .

Далее воспользовавшись формулой из физики

(2.1)

и формулами из курса математического анализа

, где , (2.2)

подставим формулы (2.2) в равенство (2.1)

, откуда .

Введем обозначение и так как с течением времени функция s(t) убывает, то оставляем знак минус

. (2.3)

Полученное равенство (2.3) проинтегрируем по t (0≤ t ≤ T), в то же время изменяется от h до 0 (h ≥≥ 0) и h – переменная величина

,

откуда

. (2.4)

Интегральное уравнение вида (2.4) есть уравнение Вольтерра первого рода, где u(x) - неизвестная функция. Решение таких уравнений впервые предложил Абель и поэтому уравнения такого вида называются уравнениями Абеля.

2. Задачи Коши для дифференциальных уравнений первого порядка

, . (2.5)

Формально проинтегрировав уравнение в задаче (2.5) с пределами интегрирования от до x получим нелинейное уравнение Вольтерра второго рода

,

которое эквивалентно задаче (2.5).

3.Задача Коши для линейных уравнений высших порядков

,, , где . (2.6)

Положим

(2.7)

тогда

,

где – любое из отрезка [a,b] при нахождении общего решения и – начальное значение при решении задачи Коши. Интегрируя далее, необходимое число раз, найдём

и по формуле Коши для кратного интегрирования имеем

,

…………………………………………………………

,

,

………………………………………………………

,

. (2.8)

Найдем дифференциальный оператор , подставив в него полученные выражения для функции и её производных

.

Введем обозначения

,

.

Тогда выражение для дифференциального оператора перепишется

и вводя обозначение g(x) = f(x) – придем к разрешающему интегральному уравнению

, (2.9)

которое эквивалентно первоначальной задаче.

4.Краевые задачи для дифференциальных уравнений

Рассмотрим линейную краевую задачу

,

, , (2.10)

где , функции и – непрерывны коэффициенты и – постоянные числа.

Как и в предыдущей задаче введем новую функцию

и выпишем выражения производных и самой функции y(x)

, (2.11)

, где .

Если в (2.11) положить , то получим и соотношения (2.11) перепишутся

. (2.12)

При из (2.11) имеем

. (2.13)

Подставляем выражения для производных (2.13) в краевые условия (2.10)

или, группируя члены с одноимёнными производными, получим систему n линейных неоднородных алгебраических уравнений с неизвестными .

. (2.14)

Обозначим определитель этой системы через

=det.

Пусть ≠ 0, тогда , обозначив через _ij миноры определителя с их знаками в алгебраических дополнениях, получим

(2.15)

.

Найдем выражение дифференциального оператора через новую функцию

(2.16)

где

_.

Подставляя выражение (2.16) в уравнение краевой задачи(2.10), придем к разрешающему интегральному уравнению смешанного типа Вольтерра-Фредгольма

где F(x) = f(x) – Ф (x).

Полученное разрешающее уравнение эквивалентно первоначально поставленной краевой задаче (2.10).

Аналогичных задач в различных областях знаний возникает множество, мы ограничимся приведёнными.