5.5. Отношение порядка
Определение: Отношение называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично, транзитивно.
Определение: Отношение называется отношением строгого порядка, если оно антирефлексивно, антисимметрично, транзитивно. Оба типа отношений называются отношениями порядка.
Определение: Элементы a, b сравнимы по отношению порядка R, если выполняется a R b или b R a.
Определение: Множество М, на котором задано отношение порядка, называется полностью упорядоченным, если любые два элемента М сравнимы.
Определение: Множество М, на котором задано отношение порядка, называется частично упорядоченным, если не любые два элемента М сравнимы.
Пример:
а) отношения
“
”
и “
”
для чисел являются отношениями нестрогого
порядка, “<” и “>” - отношениями
строгого порядка. Оба отношения полностью
упорядочивают множества N и R;
б) определим
отношения “
”
и “
”
на
:
,
если
;
,если
и хотя бы для одной
координаты (с номером i)
выполнено
.
Эти отношения определяют частичный порядок, так как, например:
и
,
но вектора
– несравнимы;
в) на системе
подмножеств множества М отношение “
”
задает нестрогий частичный порядок, а
отношение “
”
- строгий частичный порядок.
Например,
,
но
-
несравнимы;
г) отношение подчиненности на предприятии задает строгий частичный порядок; порядок частичный так как несравнимы сотрудники разных отделов;
д) Лексико - графический порядок.
Пусть в списке
букв конечного алфавита А порядок букв
зафиксирован, т. е. всегда один и тот
же, как, например, в русском и латинском
алфавите. Тогда этот список определяет
полное упорядочение букв, которое
назовем отношением предшествования и
обозначим: “
”
. (
,
если
предшествует
в списке букв).
На основе отношения предшествования букв, строится отношение предшествования слов, определяемое следующим образом:
Пусть даны слова
и
.
Тогда,
тогда и только тогда, когда
1) 
,
где
(
- слова возможно непустые,
- буквы);
2) 
,
где
- непустое слово.
Это отношение задает полное упорядочение множества всех конечных слов в алфавите А, которое является лексикографическим упорядочением слов.
Пример:
а) упорядочение слов в словарях.
Например, лес
лето:
=
“лес”; “c”
“т” и,
”0”,
поэтому “лес” в словарях - раньше
“лето”;
лес
лесть:
=
“лес”
и
,
где
=
“ть”.
б) если рассматривать числа в позиционных системах счисления (двоичной, десятичной) как слова в алфавите цифр, то их лексико - графическое упорядочение совпадает с обычным, если все сравнимые числа имеют одинаковое число разрядов.
6. Элементы общей алгебры
6.1. Алгебры
Определение:
n-арная операция на множестве М – это функция типа
,
где n-арность операции. Операция замкнута относительно множества М по определению, т. е. операция над элементами множества М, и результат тоже элемент М.
Определение:
Алгеброй
называется множество, вместе с заданной
на нем совокупностью операций
,
т. е.
система
.
Определение: М – основное (несущее) множество (носитель алгебры) алгебры А.
Определение: Тип алгебры – вектор арностей операций.
Определение: Сигнатура – совокупность операций .
Определение: Множество
называется замкнутым
относительно
n-арной
операции
на М, если
,
т. е. если значения
на аргументе из
принадлежат
.
Определение: Если
замкнуто относительно всех операций
,
алгебры М, то система
называется
подалгеброй
алгебры А (при этом
рассматриваются как операции на
).
Примеры:
1. Определение:
Алгебра
- называется полем
действительных чисел.
Обе операции
бинарные, поэтому тип этой алгебры
(2,2). Сигнатура
.
Подалгеброй этой алгебры является, например, поле рациональных чисел.
2.
Пусть
.
Определим на
операции:
- «сложение по модулю р»,
- «умножение по модулю р», следующим
образом:
и
,
где с и d
– остатки от деления на р чисел а + b
и а
b
соответственно.
Пусть, например,
р = 7, тогда
и
.
Часто обозначают: a + b = с (mod p)
a b = d (mod p).
Определение:
Конечным
полем характеристики р
называется алгебра
,
если р – простое число.
3. Пусть задано множество U.
Определение:
Булеаном U
называется множество всех подмножеств
множества U
(обозначается
).
Определение:
Булева алгебра
множеств над U
– алгебра
.
Ее тип (2,2,1), сигнатура
.
Элементами основного множества булевой алгебры являются множества (подмножества U).
Для любого
- является подалгеброй В.
Например, если
,
то основное множество алгебры В содержит
16 элементов; алгебра
- подалгебра В. Ее несущее множество
содержит четыре элемента.
4.
Множество F
одноместных функций на R,
т. е. функции
вместе с операцией дифференцирования
является алгеброй. Элементы несущего
множества – функции типа
,
единственная операция этой алгебры
дифференцирования – унарная операция
типа
(так как производной функцией на R
снова является функция на R).
Множество элементарных функций замкнуто относительно дифференцирования, поскольку произведение элементарных функций элементарно, следовательно, образуют подалгебру данной алгебры.
5.
Рассмотрим квадрат с вершинами в точках
,
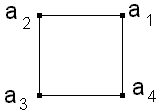
пронумерованных против часовой стрелки,
и повороты квадрата в том же направлении,
переводящие вершины в вершины. Таких
поворотов бесконечно много: на углы 0,
,
,
,
2,
,
. . . , однако они задают всего 4 различных
отображения множества вершин в себя,
соответствующие первым четырем поворотам.
- поворот на углы
0, 2,
4,...
- поворот на углы
- поворот на углы
0, 3,
5,...
- поворот на углы
Таким образом,
получаем алгебру с основным множеством
и четырьмя унарными операциями
(т. е. сигнатура алгебры
,
тип алгебры {1,1,1,1}. Их можно задать
таблицей, в которой на пересечении
строки номер
и столбца
написано значение функции
.
Определение: Тождественной операцией называется операция , отображающая любой элемент в себя. Тождественная операция соответствует нулевому повороту. Подалгебр в алгебре с одной операцией , нет.
6.
Множество
- отображение вершин в себя из предыдущего
примера (5), вместе с бинарной операцией
композиции “
”
отображений образует алгебру (L,
). Композиция отображений – это
последовательное выполнение двух
поворотов. Она задается таблицей. В
таблице на пересечении строки
и столбца
написан результат
.
Таблица Кэли
Определение:
Такая таблица, задающая бинарную
операцию, называется таблицей
Кэли. Множество
,
т. е. повороты на углы 0,
образуют подалгебру алгебры
.