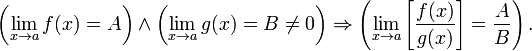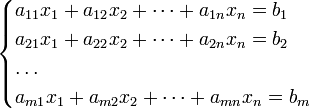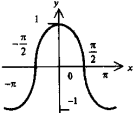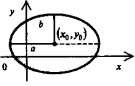- •1 Векторы
- •Свойства
- •Линейные операции над векторами ]Сложение векторов ]Сложение геометрических векторов
- •]Сложение коллинеарных скользящих векторов
- •Сложение векторов - элементов линейного пространства
- •Умножение вектора на число
- •Скалярное произведение
- •Векторное произведение
- •Смешанное произведение
- •2 Прямая Уравнения прямой на плоскости
- •Общее уравнение прямой
- •Уравнение прямой в полярных координатах
- •Тангенциальное уравнение прямой
- •Уравнения прямой в пространстве
- •Взаимное расположение нескольких прямых на плоскости
- •Некоторые характеристические свойства плоскости
- •Уравнения плоскости
- •Связанные понятия
- •Классификация кривых второго порядка Невырожденные кривые
- •Вырожденные кривые
- •Канонический вид
- •Определение через разложение по первой строке
- •Свойства определителей
- •Операции над матрицами
- •Метод Гаусса—Жордана
- •Методы решения (нажать с ctrl)
- •Непрерывная функция
Операции над матрицами
Умножение матрицы на число
Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен
![]()
Сложение матриц
Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен
![]()
Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
![]()
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю
Метод Гаусса—Жордана
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λi (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
![]() .
.
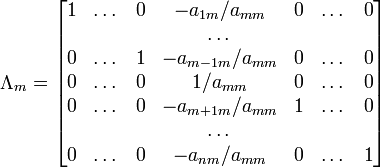 .
.
Вторая матрица после применения всех операций станет равна Λ, то есть будет искомой
7 Применение определителей и матриц
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
|
|
(1) |
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1].
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Методы решения (нажать с ctrl)
-
Метод Гаусса
-
Метод Гаусса — Жордана
-
Метод Крамера
-
Матричный метод
.
10 Элементарные функции
Графики
|
|
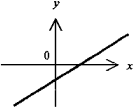
Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность) |
|
|
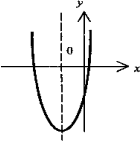
Парабола - график функции квадратного трёхчлена у = ах2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2 + bx +с =0 |
|
|
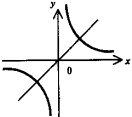
Гипербола -
график функции |
|
|
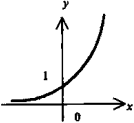
Экспонента (показательная функция по основанию е) у = еx. (Другое написание у = ехр(х)). Асимптота - ось абсцисс. |
|
|
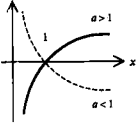
Логарифмическая функция y = logax (a > 0) |
|
|
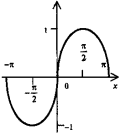
у = sinx. Синусоида - периодическая функция с периодом Т = 2π |
|
|
у = а•sin(ωx+φ) - функция гармонических колебаний. Обозначения: а - амплитуда, ω - частота (ω = 2π/Т), φ - фаза (сдвиг). |
|
|
Косинусоида
у = cosx (графики
у = sinx и у = cosx сдвинуты по оси х на |
|
|
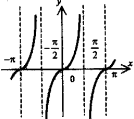
Тангенсоида
y = tgx.
Точки разрыва при х = |
|
|
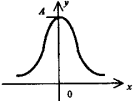
Гауссиана у = Аe-(ax2). Кривая "нормального" закона распределения ошибок, у которого
σ 2 - дисперсия ошибки. Симметрия относительно оси у. |
|
|
у
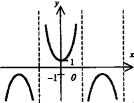
= secx -
кривая "цепной линии", эту форму
принимает абсолютно гибкая нить,
подвешенная в параллельном поле
тяжести. А полная функция периодична,
и её асимптоты х = |
|
|
Круг с центром в точке (xo, yo) радиуса r. (x-xo)2 + (y-yo)2 = r2 |
|
|
Эллипсс центром в точке (xo, yo). Большая полуось а, малая b, эксцинтриситет
|
|
|
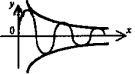
Затухающее колебание y = Ae-ax•sin(ωx+φ) |
Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
-
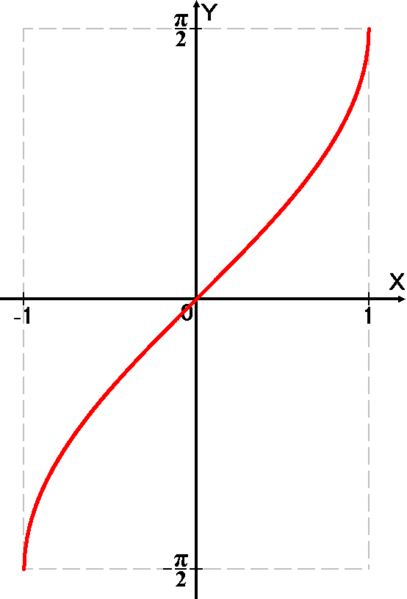
аркси́нус (обозначение: arcsin)
-
аркко́синус (обозначение: arccos)
-
аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
-
арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
-
арксе́канс (обозначение: arcsec)
-
арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)
Свойства функции arcsin
-
 (функция
является нечётной).
(функция
является нечётной). -
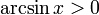 при
при  .
. -
 при x =
0.
при x =
0. -
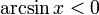 при
при 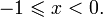
-
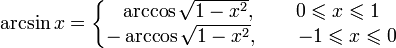
-

-
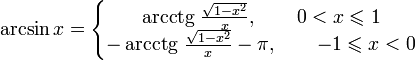
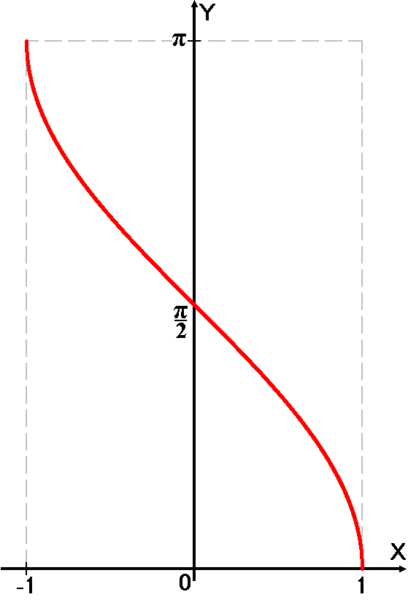
Функция arccos
![]()
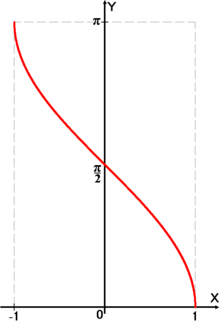
График функции y = arccos x.
Арккосинусом числа m называется
такое значение угла x,
для которого ![]()
Функция y = cos x непрерывна и на всей своей числовой прямой. Функция y = arccos x является строго убывающей.
-
cos(arccos x) = x при

-
arccos(cos y) = y при
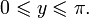
-
D(arccos x) = [ − 1;1], (область определения),
-
E(arccos x) = [0;π]. (область значений).
[править]Свойства функции arccos
-
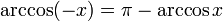 (функция
центрально-симметрична относительно
точки
(функция
центрально-симметрична относительно
точки 
-
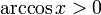 при
при 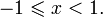
-
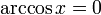 при
при 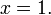
-
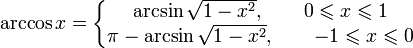
-
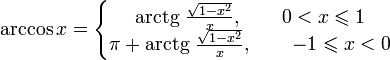
-
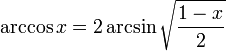
-
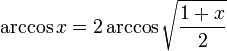
-
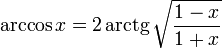
Функция arctg
![]()
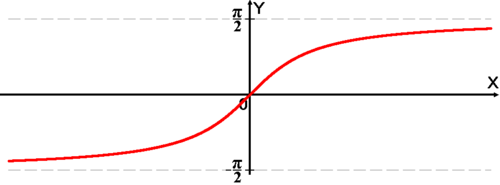
График
функции ![]() .
.
Арктангенсом числа m называется
такое значение угла α,
для которого ![]()
Функция ![]() непрерывна
и ограничена на всей своей числовой
прямой. Функция
непрерывна
и ограничена на всей своей числовой
прямой. Функция ![]() является
строго возрастающей.
является
строго возрастающей.
-
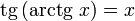 при
при 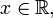
-
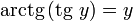 при
при 
-
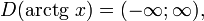
-
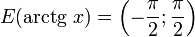
[править]Свойства функции arctg
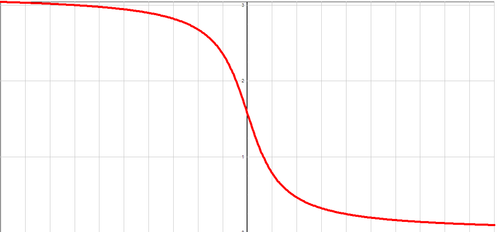
Функция arcctg
![]()
График функции y=arcctg x
Арккотангенсом числа m называется
такое значение угла x,
для которого ![]()
Функция ![]() непрерывна
и ограничена на всей своей числовой
прямой. Функция
непрерывна
и ограничена на всей своей числовой
прямой. Функция ![]() является
строго убывающей.
является
строго убывающей.
-
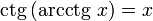 при
при 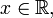
-
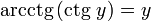 при 0
< y <
π,
при 0
< y <
π, -

-
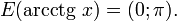
[править]Свойства функции arcctg
-
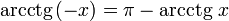 (график
функции центрально-симметричен
относительно точки
(график
функции центрально-симметричен
относительно точки 
-
 при
любых x.
при
любых x. -

11 Теория пределов
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Предел функции по Гейне
Значение ![]() называется пределом (предельным
значением)
функции
называется пределом (предельным
значением)
функции ![]() в
точке
в
точке ![]() ,
если для любой последовательности точек
,
если для любой последовательности точек ![]() ,
сходящейся к
,
сходящейся к ![]() ,
но не содержащей
,
но не содержащей ![]() в
качестве одного из своих элементов (то
есть в проколотой окрестности
в
качестве одного из своих элементов (то
есть в проколотой окрестности ![]() ),
последовательность значений
функции
),
последовательность значений
функции ![]() сходится
к
сходится
к ![]() .[1]
.[1]
![]()
Предел функции по Коши
Значение ![]() называется пределом (предельным
значением)
функции
называется пределом (предельным
значением)
функции ![]() в
точке
в
точке ![]() ,
если для любого наперёд взятого
положительного числа ε найдётся
отвечающее ему положительное число
,
если для любого наперёд взятого
положительного числа ε найдётся
отвечающее ему положительное число ![]() такое,
что для всех аргументов
такое,
что для всех аргументов ![]() ,
удовлетворяющих условию
,
удовлетворяющих условию ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .[1]
.[1]
![]()
Теоремы о пределах
Пусть
даны функции ![]() и
и ![]() .
.
-
Одна и та же функция в одной и той же точке может иметь только один предел.
![]()
Доказательство [скрыть]
![]() Доказательство
методом от противного. Пусть
существует
Доказательство
методом от противного. Пусть
существует ![]() и
и ![]() и
и ![]() .
Предположим A1 < A2.
Возьмём
.
Предположим A1 < A2.
Возьмём ![]() ,
такое что A1 +
ε < A2 −
ε,
т.е.
,
такое что A1 +
ε < A2 −
ε,
т.е. ![]() .
.
![]() ,
т.е. A1 −
ε < f(x)
< A1 +
ε.
,
т.е. A1 −
ε < f(x)
< A1 +
ε.
![]() ,
т.е. A2 −
ε < f(x)
< A2 +
ε.
,
т.е. A2 −
ε < f(x)
< A2 +
ε.
Тогда
получаем ![]() Противоречие.
Значит предел единственный.
Противоречие.
Значит предел единственный. ![]()
-
Сходящаяся функция локально сохраняет знак. Более обще,
![]()
где ![]() —
проколотая окрестность точки a.
—
проколотая окрестность точки a.
-
В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
![]()
-
Сходящаяся функция локально ограничена в окрестности предельной точки:
![]()
-
Отделимость от нуля функций, имеющих предел, отличный от нуля.
![]()
-
Операция взятия предела сохраняет нестрогие неравенства.
![]()
-
Правило двух милиционеров
-
Предел суммы равен сумме пределов:
![]()
-
Предел разности равен разности пределов:
![]()
-
Предел произведения равен произведению пределов:
![]()
-
Предел частного равен частному пределов.