Математична логіка
Математична логіка – це аналіз методів міркувань. При цьому в першу чергу досліджуються форми міркувань, а не їхній зміст.
Визначення. Висловленням називається оповідальне речення, про яке можна сказати в даний момент часу, що воно істинне або хибне, але не те й інше одночасно.
Зіставимо кожному висловленню змінну, що має значення істина - 1, якщо воно істинно, і значення хибність - 0, якщо висловлення хибне. Значення істинності складеного висловлення залежить від значень істинності складових його висловлень. Для складання складних висловлень застосовуються логічні зв'язки:
– логічне додавання (або), диз'юнкція;
– логічне множення (і), кон’юнкція;
() логічне заперечення (не).
Якщо P і Q – деякі висловлення, то можна скласти нові висловлення PQ, PQ,P,Q, причому істинність складених висловлень визначається за допомогою таблиць істинності:
|
P |
Q |
PQ |
|
P |
Q |
PQ |
|
P |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
||||
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
||
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
||
|
1 |
1 |
1 |
1 |
1 |
1 |
|
|
Властивості булевих операцій:
1. Ідемпотентність: AA=A, AA=A.
2. Комутативність: AB=BA, AB=BA.
3. Асоціативність: A(BC)=(AB)C, A(BC)=(AB)C.
4. Дистрибутивність: (C) = ()(C).
(C) = ()(C).
6.
Інволюція:
.
7. Правила
де Моргана:
8.
Склеювання:
9. Поглинання: (AB)=A, A(B)=A.
10. Закон
протиріччя:
.
11. Закон
виключеного третього:
12. Дії
з нулем і одиницею:
В логіку крім трьох основних булевих операцій для утворення складних висловлень вводять ще дві: імплікація (слідування) – (AB) («якщо A, то B»); еквівалентність – (A B) або () («якщо і тільки якщо»), що мають таблиці істинності, представлені на малюнку 2.
Л
A B AB
A B A~B 0 0
1 0 0
1 0 1 1 0 1 0 1 0 0 1 0 0 1 1 1 1 1 1
Для
кожного складного висловлення можна
побудувати таблицю істинності. Якщо
складене висловлення залежить від n
складових, то в таблиці істинності
такого висловлення буде
рядків.
Приклад.
Побудувати таблицю істинності висловлення,
представленого формулою:
.
|
A |
B |
C |
|
|
( |
|
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
B
B)CВизначення. Складене висловлення, що істинне незалежно від значень висловлень, що входять у нього, називається тавтологією, таблиця істинності тавтології містить тільки значення “істинно”, а його функція тотожно дорівнює одиниці. Складене висловлення, що хибне незалежно від значень висловлень, що входять у нього, називається протиріччям.
Щоб
перевірити, чи є висловлення тавтологією
або протиріччям, треба скласти для неї
таблицю істинності з
рядків на всіх наборах значень змінних,
або ж перевірити за допомогою еквівалентних
перетворень.
У численні висловлень формули будуються за наступними правилами:
-
змінна є формула;
-
якщо F і P – формули, то формулами будуть також
,
,
,
,
,
; -
інших формул немає.
Визначення. Формули, що представляють ту саму функцію, називаються еквівалентними або рівносильними.
Приклад.
Штрих Шеффера:
;
стрілка
Пірса:
.
Для спрощення формул використовують властивості булевих операцій, а також наступні три тотожності, що дозволяють замінити імплікацію () і еквівалентність () булевими операціями:
13)
14)
15)
.
Правила спрощення формул такі:
-
за допомогою формул 14 і 15 виключити з формули еквівалентність;
-
за допомогою формули 13 виключити імплікацію;
-
за правилами де Моргана опустити заперечення формул до рівня змінних (властивість 7);
-
застосувати тотожності дистрибутивності (властивості 4, 5);
-
привести подібні.
Приклад.
{формули
13, 14}
{властивості 4, 5}
{властивість 10}
{властивості
4, 5}=
{властивості 1, 2}=
{властивості
9, 12}
{властивості
4, 2}=
{властивість 12}
.
Введемо
позначення:
.
Тоді, якщо позначити через
змінну, що приймає значення 0 або 1, то
справедливе співвідношення
(
).
Теорема.
Усяку логічну функцію n змінних
можна представити у вигляді
,
де диз'юнкція береться по всім тим наборам змінних, при яких f=1.
Це розкладання функції по n змінним називається досконалою диз'юнктивною нормальною формою (ДДНФ) функції f. ДДНФ функції f містить рівно стільки кон’юнкцій, скільки одиниць у таблиці істинності f.
Зауваження.
Для нуля не існує ДДНФ:
;
для одиниці ДДНФ є:
.
Кожна
функція
P2
(множини логічних функцій n змінних),
причому така, що
,
має ДДНФ, що будується в такий спосіб:
у таблиці істинності виділяють ті рядки,
тобто ті набори змінних
,
для яких
.
Для кожного позначеного рядка утворюють
кон’юнкцію
.
Складають диз'юнкцію всіх отриманих
кон’юнкцій.
П
риклад.
Побудувати ДДНФ для функції
,
заданої таблицею істинності.
Розв’язання.
Тут “”
відзначені ті набори змінних
,
для яких
,
у цих рядках складено елементарні
кон’юнкції. ДДНФ для f має вигляд:
.
Визначення. Елементарною кон’юнкцією називається кон’юнкція змінних або їхніх заперечень, у яку кожна змінна входить не більш одного разу. Диз'юнкція елементарних кон’юнкцій називається диз'юнктивною нормальною формою (ДНФ).
Приклад.
(ДНФ);
(СДНФ)
Різниця між ДНФ і ДДНФ полягає в тому, що в ДДНФ кожна елементарна кон’юнкція містить усі n змінних або їхніх заперечень, у той час як у ДНФ деякі змінні можуть бути відсутні. У той час як для кожної функції ДДНФ існує єдина, ДНФ для тієї ж функції існує зліченна множина.
Диз'юнктивну нормальну форму, у тому числі і досконалу, можна побудувати за допомогою еквівалентних перетворень по наступному алгоритму:
а) виключити “” і “” за допомогою формул 13-15;
б) за допомогою правил подвійного заперечення і де Моргана виключити заперечення над операціями;
в) розкрити дужки і застосувати властивість ідемпотентності, закони виключеного третього і протиріччя;
г) виключити константи по властивостях 12.
Правило побудови ДДНФ по ДНФ. Усяку ДНФ можна привести до ДДНФ розщепленням кон’юнкцій до всіх змінних, тобто елементарні кон’юнкції, у які співмножниками входять не всі змінні, множать на одиниці, представлені у вигляді диз'юнкцій кожної відсутньої змінної і її заперечення (закон «виключеного третього»), і розкривають дужки за законом дистрибутивності 4. Нарешті, виключають повторення доданків.
Приклад. Дану формулу привести до ДНФ і ДДНФ за допомогою еквівалентних перетворень.
.
Розв’язання.
{формули
13, 14}
{властивості
4, 5, 1} = =
{властивості 4, 5} =
{властивість
10} =
– отримана ДНФ для функції, представленої
формулою
.
Приведемо тепер ДНФ до ДДНФ за описаним правилом.
{додамо
змінну A у третю кон’юнкцію}
{ по властивості 4}
{властивості 2, 1 приводять до ДДНФ}=
.
Визначення. Елементарною диз'юнкцією називається диз'юнкція змінних або їхніх заперечень, у яку кожна змінна входить не більш одного разу. Кон’юнктивною нормальною формою (КНФ) називається формула, представлена у вигляді кон’юнкції елементарних диз'юнкцій.
Приклад.
–
кон’юнктивні нормальні форми для
функції трьох змінних.
Кожна формула алгебри висловлень має множину різних КНФ.
Визначення. Досконалою кон’юнктивною нормальною формою (ДКНФ) формули алгебри висловлень називається КНФ, у якій:
-
кожен співмножник містить доданками всі змінні, причому кожну тільки один раз із запереченням або без;
-
відсутні повторення співмножників.
За допомогою еквівалентних перетворень будь-яка формула приводиться до КНФ аналогічно її приведенню до ДНФ. В отриманій КНФ до елементарних диз'юнкцій, у які доданками входять не всі змінні, додати нулі, представлені у вигляді кон’юнкцій кожної відсутньої змінної і її заперечення (закон протиріччя), і за допомогою закону дистрибутивності диз'юнкції відносно кон’юнкції (властивість 5) привести ці співмножники до сум першої степені, тобто сум, що не містять добутків. Нарешті, виключити повторення співмножників.
Приклад.
–
ДКНФ.
У табличному способі розглядаються тільки ті рядки таблиці істинності, де функція приймає значення 0. Кожному такому рядкові відповідає диз'юнкція всіх змінних, причому аргумент, що приймає значення 0, береться без заперечення, а той, що приймає значення 1, – із запереченням. Нарешті, утворюють кон’юнкцію отриманих диз'юнкцій.
П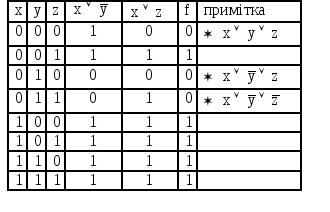
риклад.
Привести до ДКНФ формулу
.
Розв’язання.
ДКНФ для функції f має вигляд:
Зауваження.
Кожна функція алгебри висловлень має
єдину ДКНФ. Функція, що тотожно дорівнює
одиниці, не має ДКНФ:
.
Для нуля ДКНФ існує і має вигляд:
.
Алгебра Жегалкіна.
Алгебра
Жегалкіна – це алгебра булевих функцій,
утворених за допомогою булевої константи
1, булевих змінних та булевих функцій:
1) + − сума за модулем 2, 2)
− кон’юнкція.
Властивості операцій в алгебрі Жегалкіна:
1)
,
,
2)
,
,
3)
,
4)
,
,
5)
,
,
6)
.
У силу
повноти системи
будь-яку функцію можна надати у вигляді
многочлена від своїх змінних, який
називається поліномом Жегалкіна. Поліном
Жегалкіна має вигляд:
,
(1)
де
,
.
Зауваження. Добутки, які відрізняються тільки порядком множників, вважають рівними.
Число
різних поліномів Жегалкіна від
змінних дорівнює
,
та дорівнює числу різних булевих функцій
від
змінних. Тому надання булевої функції
поліномом Жегалкіна єдине.
Приклад.
Виразити
у вигляді полінома Жегалкіна.
Розв’язання.
Перший спосіб знаходження полінома – це метод невизначених коефіцієнтів.
|
|
|
|
Знаходження коефіціентів |
|
0 |
0 |
0 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
1 |
|
|
1 |
1 |
1 |
|
,
,
,
,
Звідки,
.
Надання
функції
у вигляді (1) називається також досконалою
поліноміальною нормальною формою
(ДПНФ).
Тотожні співвідношення для алгебри Жегалкіна:
1)
,
2)
,
3)
,
4)
,
5)
.
Алгоритм побудови ДПНФ:
-
В ДДНФ операцію
можна
замінити на + , -
В усіх кон’юнкціях можна зробити заміну
,
а далі, розкрити дужки та привести
подібні за правилами
,
.
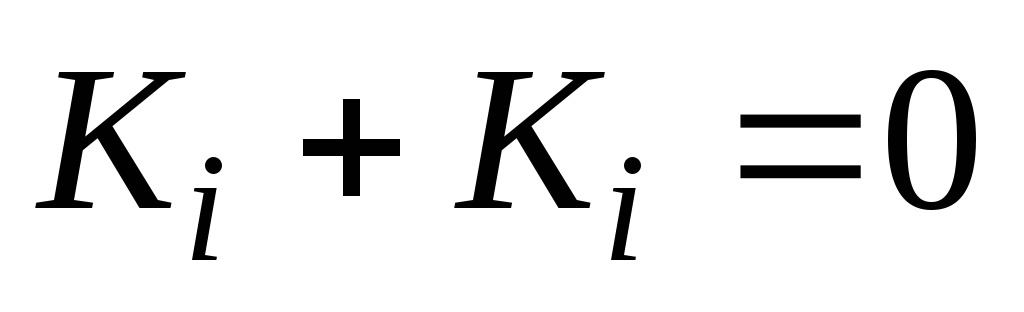В результаті буде побудована ДПНФ.
Приклад. Побудувати многочлен Жегалкіна, для функції, яка задана таблицею.
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
.
Приклад. Знайти поліном Жегалкіна без застосування ДДНФ.
Розв’язання.
1)
,
2)
