73

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Запорізький національний технічний університет

МЕТОДИЧНІ ВКАЗІВКИ

до виконання контрольних робіт та самостійної роботи

для студентів факультету ІОТ заочної форми навчання

з дисципліни “ДИСКРЕТНА МАТЕМАТИКА”

2011

Методичні вказівки до виконання контрольних робіт та самостійної роботи для студентів факультету ІОТ заочної форми навчання з дисципліни “Дискретна математика” / Укл.: Т.І. Левицька,  І. С. Пожуєва,  О. Л. Мізерна. – Запоріжжя: ЗНТУ, 2011. - 100 с.

Укладачі: Т.І. Левицька, доцент, к.т.н.

І. С. Пожуєва, доцент, к.т.н.

О.Л. Мізерна, асистент.

Експерт

спеціальності: М.М. Касьян, доцент, к.т.н.

Рецензент: В. С. Левада, доцент, к.т.н.

Відповідальний

за випуск: І. С. Пожуєва, доцент, к.т.н.

Затверджено радою РП факультету ЗНТУ Протокол № від

Затверджено на засіданні кафедри прикладної математики ЗНТУ Протокол № від

ЗМІСТ

Вступ 4

Теоретичні питання 5

ІНДИВІДУАЛЬНІ ЗАВДАННЯ 11

Література 71

Вступ

Завдання до контрольних робіт складені у відповідності до програми з курсу дискретна математика багатоступеневої підготовки фахівців і призначені для студентів заочної форми навчання, що навчаються на факультеті інформатики і обчислювальної техніки.

У вказівках приведені основні теоретичні данні та формули, приклади розв’язування задач. Приведено 25 варіантів контрольних робіт, кожне з котрих має практичні задачі за темами: множини, комбінаторика, графи та математична логіка, що відповідає програмі з курсу дискретна математика для спеціальностей факультету ІОТ. Номер варіанту визначається за останніми двома цифрами номера залікової книжки студента.

Множини, дії над множинами. Відношення.

Визначення. Множина – це сукупність деяких об’єктів (елементів множини), виділених за певною ознакою з інших об’єктів. При цьому повинно бути дано повний опис класу всіх об’єктів, які розглядаються (універсальна множина ). Факт належності елемента множині позначається . Запис означає, що елемент універсальної множини не належить множині . Якщо для всіх елементів множини і тільки для них виконується властивість , то це позначають . Інколи вдається перелічити всі елементи множини . Тоді наводять повний перелік усіх різних елементів множини: .

Множина, яка не має жодного елемента, називається порожньою і позначається .

Визначення. Якщо кожен елемент множини є елементом множини , то називається підмножиною множини , що позначають . Вважається, що порожня множина є підмножиною будь-якої множини, а також .

Визначення. Множина всіх підмножин множини називається булеаном і позначається . Потужність скінченної множини дорівнює кількості її елементів, позначається . Потужність порожньої множини дорівнює 0.

Якщо , то .

Приклад. .

Приклад. Знайти булеан множини .

Розв’язання.

Потужності множин , . Булеан має вигляд .

Визначення. Дві множини і рівні між собою, якщо і .

Над множинами можна виконувати дії: об’єднання, переріз, доповнення, різницю, симетричну різницю, декартів добуток.

Визначення. Об’єднання , переріз , доповнення , різниця , симетрична різниця . Тут використано логічні знаки: - «або», - «і».

Приклад. Виконати дії над множинами і .

Розв’язання.

, , , .

Приклад. Довести, що для довільних множин А і В виконується тотожність .

Розв’язання.

Нехай . Таким чином, доведено, що . Повторюючи міркування в зворотному порядку, одержимо , що доводить тотожність.

Пріоритет виконання операцій у спадному порядку – доповнення, переріз, об’єднання, різниця, симетрична різниця.

Приклад. Зобразити на діаграмі Ейлера-Вена множину, яку задано за допомогою операцій: .

Розв’язання.

З врахуванням порядку виконання операцій: 1) (мал.1), 2) (мал.2), 3) (мал.3), 4) (мал.4).

Мал.1 Мал.2 Мал.3 Мал.4

Приклад. За допомогою дій над множинами описати множину, зображену на мал.5.

Розв’язання.

Виділена частина є об’єднанням п’ятьох частин. Опишемо кожну окремо: 1)., 2)., 3)., 4)., 5).. Тому результат буде мати вигляд () ()()() ().

Мал.5

Закони алгебри множин:

1. , комутативність;

2. , асоціативність;

3. ,

дистрибутивність;

4. , властивості порожньої множини;

5. , властивості універсума;

6. , властивості доповнення;

7. , іденпотентність;

8. інволюція;

9. , закони де Моргана;

10. , закон поглинання;

11. заміна різниці;

12. заміна симетричної різниці.

Приклад. Спростити вираз, використовуючи закони алгебри множин .

Розв’язання.

.

Визначення. Декартів добуток множин А і В (позначається ) – це множина всіх упорядкованих пар елементів , де , . При цьому вважається, що тоді і тільки тоді, коли , .

Потужність декартова добутку дорівнює .

Приклад. Довести тотожність

.

Розв’язання.

Нехай

.

Визначення. Бінарним відношенням називається підмножина декартова добутку ( тобто ).

Якщо пара належить відношенню , то пишуть , або .

Областю визначення бінарного відношення називається множина , а областю значень – множина (- існує ).

Для скінчених множин бінарне відношення зручно задавати за допомогою матриці відношення , де , . Елементами матриці є значення .

Приклад. Знайти матрицю відношення , де , , - множина цілих чисел.

Розв’язання.

Згідно з означенням матриці відношення, розв’язок має вигляд

		{-1}	{0}	{1}	{-1,0}	{-1,1}	{0,1}	{-1,0,1}
-1	0	1	0	0	1	1	0	1
0	0	0	1	0	1	0	1	1
1	0	0	0	0	0	1	1	1

Приклад. Зобразити відношення графічно, де - множина дійсних чисел, та знайти його область визначення та область значень:

1) ;

2) .

Розв’язання.

Зображення відношення зводиться до графічного розв’язання системи нерівностей . Розв’язок цієї системи зображено на мал. 6. Область визначення та область значень дорівнюють .

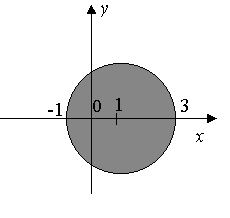
Мал.6 Мал.7

Для побудови області, яка відповідає відношенню , знаходимо границю цієї області , або . Це є рівняння кола з центром в точці (1; 0) і радіусом 2. Тому відношенню відповідає частина площини, зображена на мал. 7. Область визначення , область значень .