1.Сложение матриц. Умножение матрицы на число. Свойства операций.

Опр.1: А,ВР_mn , то сумма А, В – матрица С=А+В для которой c_ij=a_ij+b_ij.

Опр.2: АР_mn, R, то произведение А на  -матрица С=В, для которой c_ij=a_ij

Св-ва операций:

1.  А,ВР_mn: А+В=В+А (коммутативность)

2.  А,ВР_mn: А+(В+С)=(А+В)+С (ассоциативность)

3.  АР_mn: А+=А (сущ. Нулевого элемента)

4.  АР_mn,  (-А)Р_mn: А+(-А)= (сущ. обр. матрицы)

5. (+)А=А+А (дистрибут. отн. слож. чисел)

6. (А+В)=А+В (дистрибут. отн. слож. матр.)

7. ()А=(А) (ассоциат. отн. умнож. на число)

2. Произведение матриц. Свойства произведения.

Опр.1 Пусть АР_mn , BP_np, тогда произведение –матрица АВ=СР_mp такая, что

Св-ва произведения.

1. А(ВС)=(АВ)С- ассоциат.

2. (А+В)С=АС+ВС- дистрибут.

3. А(В+С)=АВ+АС- дистрибут.

4. (АВ)^Т=B^ТA^Т- транспонир.

Замечание: АВВА

Док-во:

1. АР_mn,, CР_pq,, BР_np,

2, 3

4.

3.Перестановки, инверсии и транспозиции.

А={a₁,a₂,…,a_n} –n элементное мн-во (a_ia_j)

Опр.1Перестановка (П)–упорядоченный набор элементов А

Трм.(о числе перестановок)

Число перестановок n-элементного мн-ва P_n=n!

Док-во

Метод мат. индукции

1. n=1- очевидно

2. n=k P_k=k!

a₁ ,a₂,…,a_k ,a_k+1

P_k+1=(k+1)P_k=(k+1)!

Опр.2 Если в перестановке a_i>a_j при i<j, то a_i, a_j образуют инверсию (И)

Если число инверсий в перестановке –J(П)-четно (нечетно), по перестановка называется четной (нечетной).

Опр.3 Транспозиция (Т)—операция перемены местами 2-х чисел в перестановке.

4.Теорема о транспозиции. Четность перестановки.

А={a₁,a₂,…,a_n} –n элементное мн-во (a_ia_j)

Опр.1 Если в перестановке a_i>a_j при i<j, то a_i, a_j образуют инверсию (И)

Если число инверсий в перестановке –J(П)-четно (нечетно), по перестановка называется четной (нечетной).

Трм.(о транспозиции)

Всякая транспозиция меняет четность перестановки.

Док-во:

1. Соседняя транспозиция

П₁=a₁, a₂,…, a_i, a_i+1,…, a_n

П₂=a₁, a₂,…, a_i+1, a_i,…, a_n

J(П₂)=J(П₁)+1, если a_i<a_i+1

J(П₂)=J(П₁)-1, если a_i>a_i+1

2. Произвольная транспозиция.

П₁=a₁, a₂,…, a_i,…, a_i+k,…, a_n

П₂=a₁, a₂,…, a_i+k,…, a_i,…, a_n

П₂ получается из П₁ с помощью 2k-1 соседних транспозиций.

5. Понятие подстановки. Четность подстановки. Всякое взаимно однозначное отображение множества первых n натуральных чисел на себя называется подстановкой n-й степени, причем всякая подстановка А может быть записана при помощи двух перестановок, подписанных одна под другой , здесь через _i обозначается то число, в которое при подстановке А переходит число i, i=1, 2, …, n.

При всех записях подстановки А четность верхней и нижней строк либо совпадают, либо при всех записях они противоположны. В первом случае подстановка А будет называться четной, во втором – нечетной.

6. Определитель n- го порядка: определение и свойства.

Опр: Пусть AP_n^2. Определитель матрицы A – число detA = |A| = где i_1...i_n – перестановка, а s – число инверсий в ней, и j₁...j_n – перестановка, а r – число инверсий в ней.

Св-ва: 1. |A| = |A^T| 2. Если A получена из В переменой местами двух строк, то detA = -detB. 3. Если в А есть одинаковые строки, то detA=0 4. Линейность: 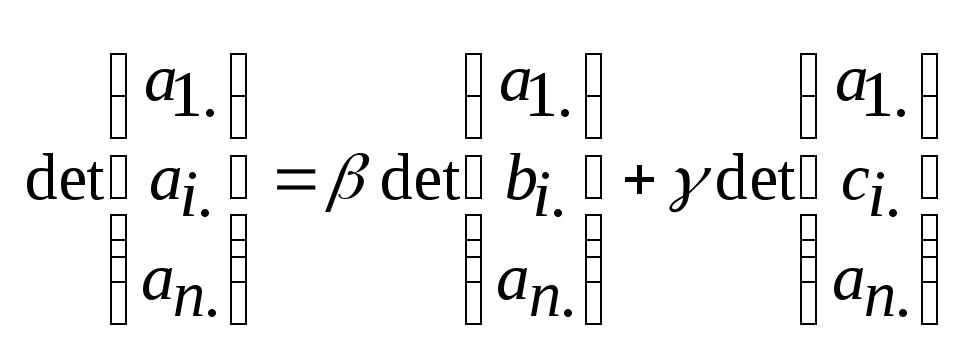, где a_i. = βb_i. + γc_i. 5. если в матрице есть 0вая строка, то ее определитель равен 0. 6. Если в А какая-либо строка представляет из себя л.к. других, то detA=0 7. Если к какой либо строке матрицы прибавить л.к. из других строк, ее определитель не изм-ся.Д-во (Док-ва св-в 5-7 следуют из св-ва 4.) 1.Следует из опредления. 2. A = ; B = ; Общий член A = ему соотв-т общ.член В = ; главный член получен с помощью перестановки, значит, он будет менять знак, значит, каждый член будет менять знак, значит определитель поменяет знак, чтд. 3. положим в в усл-ях св-ва 2 a_i = a_j. тогда по св-ву два имеем detA=-detB но в тоже время очевидно, что detA = detB. Это возможно лишь если detA=detB=0; 4. Для док-ва разложим каждый из определителей по i-той строке и заметим, что все миноры элементов i-той строки одинаковы. А отсюда следует, что доказываемая формула непосредственно вытекает из равенства a_i. = βb_i. + γc_i.