МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «Московский государственный индустриальный университет» (ФГБОУ ВПО «МГИУ»)

Кафедра деталей машин _ ________________________________________________________________

РАБОЧАЯ ТЕТРАДЬ СТУДЕНТА
по дисциплине «Детали машин и основы конструирования» _________________________________________________________________
на тему «Привод ленточного конвейера»
Группа	___________
Студент	_____________	И.О. Фамилия
Руководитель работы, должность, звание	_____________	И.О. Фамилия
ДОПУСКАЕТСЯ К ЗАЩИТЕ
Должность, ученая степень, звание	_____________	И.О. Фамилия
Оценка работы Дата	________	«___» ___________

МОСКВА 2011

Расчет привода ленточного конвейера с прямозубым цилиндрическим редуктором и клиноременной передачей*

Рассчитать привод ленточного конвейера по схеме рис. 2 с прямозубым цилиндрическим редуктором по следующим данным:

• Окружное усилие на ведущем барабане конвейера F_t = Н

• Скорость ленты конвейера (окружная скорость на барабане) V = м/с

• Диаметр барабана D_бар = м

• Время работы в сутки t_сут= час, t = час,

= t_сут – t = час.

• Отношение = ; Т_пуск= (К_пуск = )

1. Частота вращения барабана конвейера:

n_бар = = мин^-1

2. Мощность на приводном валу конвейера:

Р_потр = = кВт

3. Мощность на валу электродвигателя:

Р_{эл.двиг. потр} = = кВт

где η_общ = η_{кл. рем} ∙ η³_подш ∙ η_зац ∙ η_муфты =

Значения η_{кл. рем}, η_подш, η_зац, η_муфты выбраны из таблицы 2.

*Ссылки даются на методическое пособие В.Г. Клокова «Детали машин. Курсовое проектирование» Москва 2007.

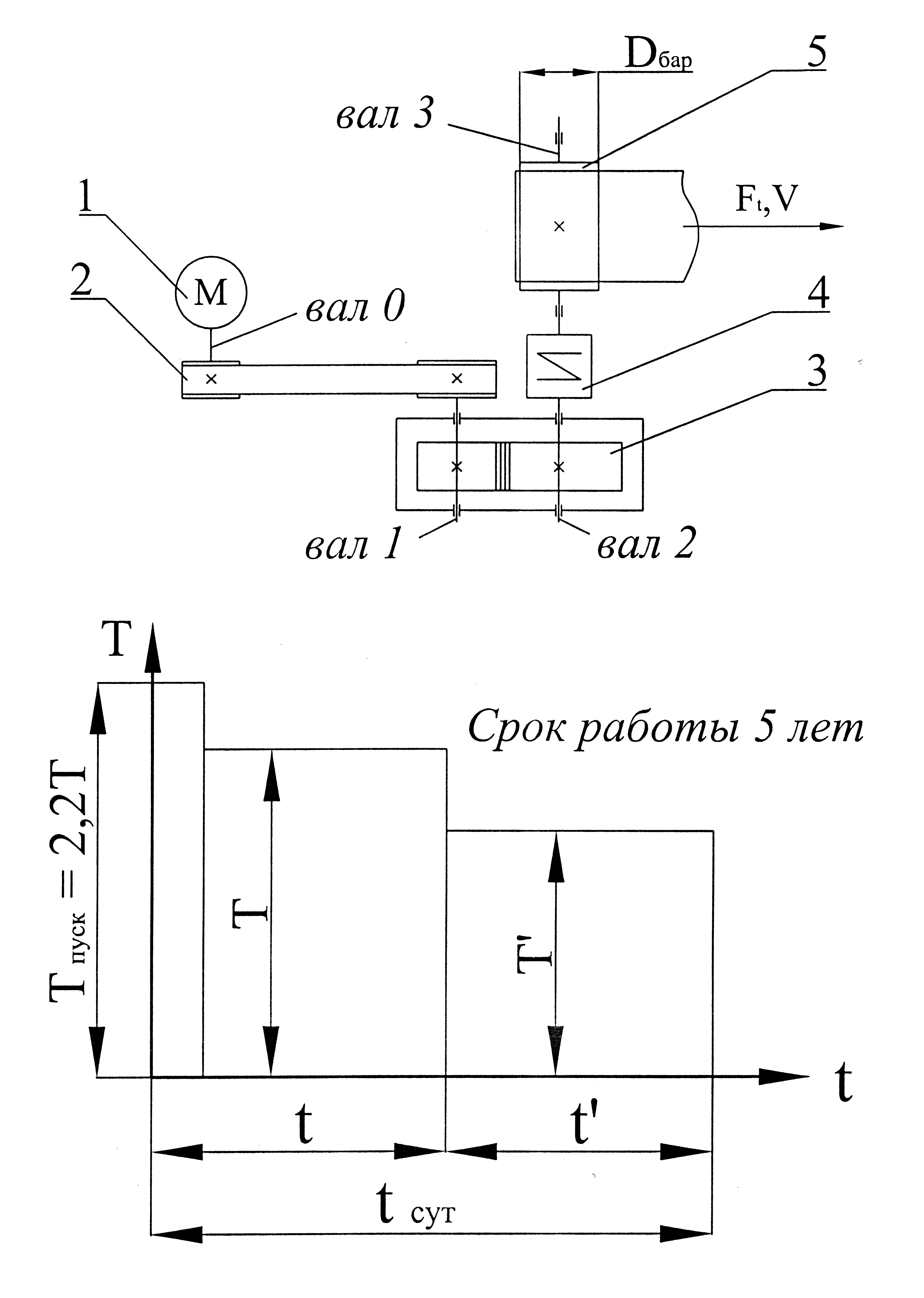
Рис. 2. Привод ленточного конвейера с прямозубым редуктором:

1 – электродвигатель; 2 – передача клиноременная; 3 – редуктор горизонтальный; 4 – муфта комбинированная; 5 – барабан приводной

Выбираем по каталогу электродвигатели, удовлетворяющие по мощности (табл. П1), т.е. с мощностью Р=

4. Передаточные числа привода и редуктора.

U_{привода} = ; U_{привода} = U_ред ∙ U_кл.рем

Принимаем предварительное значение U_ред.= ,

тогда

Uпривода
Uпривода 1 ==
Uпривода 2 ==
Uпривода 3 ==
Uпривода 4 ==

U_{кл.рем.пер.}

U_{кл.рем.пер.1} ==

U_{кл.рем.пер. 2} = =

U_{кл.рем.пер. 3} ==

U_{кл.рем.пер. 4} ==

В соответствии с рекомендациями таблицы 1 для клиноременной передачи выбираем значение

U_{кл.рем.пер.} =

5. Частоты вращения валов:

п₀ = п_{эл.двиг} = мин ^-1

п₁ = = мин ^-1

п₂ = = мин ^-1

п₃ = п₂ = мин ^-1

6. Мощности на валах:

Р₀ = Р_{эл.двиг.потр} = кВт

Р₁ = Р₀ · η_кл.рем · η_подш = кВт

Р₂ = Р₁ · η_зац · η_подш = кВт

Р₃ = Р₂ · η_муф · η_подш = кВт

7. Вращающие моменты на валах:

Т₀ = 9550= Н∙м

Т₁ = 9550= Н∙м

Т₂ = 9550= Н∙м

Т₃ = 9550 = Н∙м

Полученные результаты заносим в таблицу:

№ вала	n, мин-1	Р, кВт	Т, Н·м
0
1
2
3

8. Эквивалентное время работы передачи в сутки при расчете на контактную прочность (из циклограммы задания):

t_НЕ = t + t′ = час

Эквивалентное время работы передачи в течение всего срока службы:

Т_НЕ = t_НЕ ∙ д∙ L = час

где д = 260 – число рабочих дней в году;

L = 5 лет – срок работы передачи.

8. Эквивалентное число циклов нагружения зубьев колеса и шестерни:

N_{НЕ 2} = 60 ∙ п₂ ∙ Т_НЕ = циклов

N_{НЕ 1} = N_{НЕ 2} ∙ U_ред = циклов

8. Выбор материала шестерни и колеса.

Принимаем по таблице 5 для шестерни сталь______________ с σ_в = МПа; σ_т = МПа; НВ =

Термообработка:

Для колеса в соответствии с рекомендациями:

НВ_2min = HB_1min – (15)(20…30)(50),

подбираем по таблице 5 сталь_____________ с σ_в = МПа; σ_т = МПа; НВ =

Термообработка:

11. Средняя твердость шестерни:

НВ₁ = =

Средняя твердость колеса:

НВ₂ = =

При средней твердости шестерни НВ₁ базовое число циклов нагружения N_{HG 1}= , а для колеса при НВ₂ = базовое число циклов нагружения N_{HG 2=}

(таблица 6).

Поскольку N_{HЕ 2} > N_{HG 2} и N_{HЕ 1} > N_{HG 1}, то = 1

12. Предел контактной выносливости для колеса:

σ_{Н lim2} = 2НВ₂ + 70 =

Допускаемое контактное напряжение для колеса:

[σ]_Н2 = =

Предел контактной выносливости для шестерни:

σ_{Н lim1} = 2НВ₁ + 70 =

Допускаемое контактное напряжение для шестерни:

[σ]_Н1 = =

Коэффициент безопасности S_Н = 1,1

Расчет ведем по меньшему значению допускаемых контактных напряжений, т.е. по [σ]_Н2 =

12. Межосевое расстояние для прямозубой передачи.

Принимая предварительно К_н = 1,3 и задаваясь значениями = 0,4 и =0,5, находим два значения a_w по формуле:

a_w = 450 (U + 1) = мм

a_w = мм

Одно из найденных межосевых расстояний округляем до ближайшего стандартного значения:

a_{w ст} =

12. Ширина зубчатых колес:

b₂ = ∙ a_{w ст}=

b₁ = b₂ + 5 мм =

15. Модуль передачи:

0,01 ∙ a_{w ст} < т < 0,02 ∙ a_{w ст} = мм

Принимаем т _ст = мм

16. Суммарное число зубьев прямозубой передачи:

Z_∑ = = округлить до целого числа

Z_∑ =

16. Число зубьев шестерни:

Z₁ = = округлить до целого числа

Z₁ =

16. Число зубьев колеса:

Z₂ = Z_∑ – Z₁ =

16. Уточнение передаточного числа:

U′ = =

Отклонение от принятого ранее передаточного числа:

∆U = =

что находится в пределах допустимого [∆U] = .

16. Геометрические размеры колес.

Делительный диаметр шестерни:

d₁ = т_ст · Z₁ = мм

Делительный диаметр колеса:

d₂ = т_ст · Z₂ = мм

Межосевое расстояние:

а_{w ст} = = мм

Диаметр вершин зубьев шестерни:

d_a1 = d₁ + 2m_ст = мм

Диаметр вершин зубьев колеса:

d_a2 = d₂ + 2m_ст = мм

Диаметр впадин зубьев шестерни:

d_f1 = d₁ – 2,5m_ст = мм

Диаметр впадин зубьев колеса:

d_f2 = d₂ – 2,5m_ст = мм

16. Проверочный расчет на контактную прочность:

σ_Н = МПа

= ≤ МПа

Отклонение от [σ]_Н:

∆σ = =

при допускаемом отклонении –5% < [∆σ] < 15%.

Условие прочности выполняется.

16. Проверка зубьев на изгиб.

Эквивалентное время работы передачи в сутки при расчете на изгиб:

t_FЕ = t + t ′= час

16. Эквивалентное время работы передачи в течение всего срока службы при расчете на изгиб:

Т_FЕ = t_FЕ ∙ д ∙ L = час

16. Эквивалентное число циклов нагружения зубьев колеса:

N_FЕ2 = 60 ∙ п₂ ∙Т_FЕ = циклов

Таким образом, передача работает при постоянной нагрузке, т.к.

N_{FE 2} > N_{FG 2} = и = 1

16. Допускаемые напряжения изгиба [σ]_F.

Предел изгибной выносливости для зубьев шестерни:

σ_{F lim 1} = 1,8НВ₁ = МПа

Предел изгибной выносливости для зубьев колеса:

σ_{F lim 2} = 1,8НВ₂ = МПа

Допускаемые напряжения изгиба для шестерни:

[σ]_F1 = = МПа

Допускаемые напряжения изгиба для колеса:

[σ]_F2 = = МПа

где коэффициент безопасности S_F = 1,75, а коэффициент режима работы для нереверсивной передачи Y_А =1.

16. Окружное усилие на колесе:

F_t2 = = Н

16. Коэффициент формы зубьев при расчете на изгиб по местным напряжениям Y_FS для прямозубых передач определяют в зависимости от Z из таблицы 10:

Y_FS1 = (при Z₁ = );

Y_FS2 = (при Z₂ = ).

Напряжения изгиба зубьев для прямозубых передач.

Расчет на изгиб производится для той зубчатки, у которой отношение меньше.

Для шестерни: =

Для колеса: =

Для колеса это отношение меньше, поэтому расчет ведем по зубу колеса по формуле:

σ_F2 = = ≤ [σ]_F2 МПа

Принимаем коэффициент нагрузки при расчете на изгиб:

K_F = K_Fβ · K_FV · K_Fα

Значение K_Fβ выбираем из таблицы 11 в зависимости от коэффициента ширины шестерни относительно диаметра

(см. п. 13):

= K_Fβ =

Значение K_FV выбираем из таблицы 12 для передач с НВ < 350 в зависимости от степени точности и окружной скорости:

V = = м/с

При 8-й степени точности K_FV = 1,1.

Значение K_Fα выбираем из таблицы 13:

K_Fα =

Тогда K_F = K_Fβ · K_FV · K_Fα =

Напряжение изгиба для зубьев колеса:

σ_F2 = МПа

Поскольку σ_F2 = < [σ]_F2 = , то условие прочности выполняется.

16. _{Расчет на кратковременные перегрузки.}

• _{По контактным напряжениям}

_{Максимальное допускаемое контактное напряжение при пусковой перегрузке:}

[σ]_{Н mах2} = 2,8 ∙ σ_т = МПа

_{где σт = МПа – для материала колеса (из РГР №1).}

_{Максимальное контактное напряжение, возникающее во время пуска:}

σ_{Н mах2} = σ_Н2 ∙ = МПа

Поскольку σ_{Н max2} = < [σ]_{Н mах2} = , то условие прочности выполняется.

• _{По напряжениям изгиба}

_{Максимальное допускаемое напряжение изгиба при пусковой перегрузке:}

[σ]_{F mах 2} = 2,74 ∙ НВ₂ = МПа

_{Максимальное напряжение изгиба, возникающее во время пуска:}

σ_{F mах 2} = σ_F2 ∙ = МПа

Поскольку σ_{F max2} = < [σ]_{F mах2} = , то условие прочности выполняется.

Отношение берется из циклограммы нагрузки в задании.