§ 10 Розв’язання тригонометричних рівнянь
Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
Деякі тригонометричні рівняння шляхом тотожних перетворень можна привести до рівняння з однією тригонометричною функцією, потім зробити заміну і привести рівняння до квадратного.
Приклад 1.
Розв’язати рівняння
.
Розв’язання
Нехай
,
тоді
.
Звідси
,
.
Оскільки
,
то
,
.
Оскільки
,
то
,
.
Відповідь:
;
;
.
Приклад 2.
Розв’язати
рівняння
.
Розв’язання
Замінивши
на
,
матимемо:
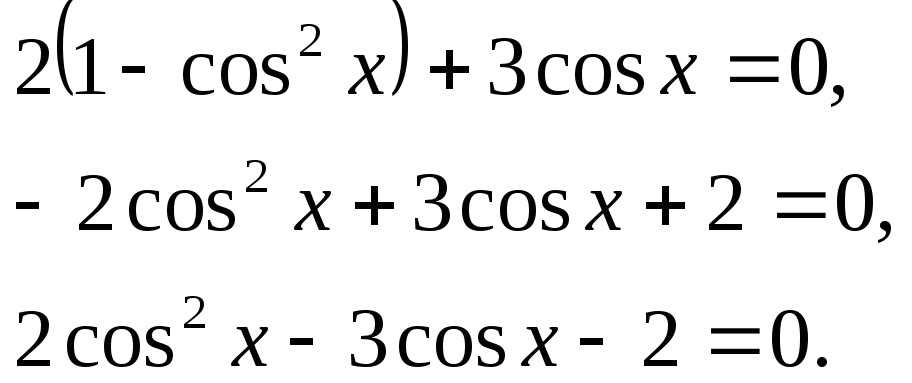
Нехай
,
тоді
.
Звідси
,
.
Оскільки
,
то рівняння
розв’язків немає.
Оскільки
,
то
,
Отже
Відповідь:
Приклад 3.
Розв’язати
рівняння
,
Розв’язання
,
.
Нехай
,
тоді
,
,
.
Маємо: 1)
,
.
2)
,
.
Відповідь:
.
59. Розв’язати рівняння:
1)
,
2)
,
3)
,
4)
,
5)
,
6)
,
7)
,
8)
,
9)
,
10)
,
11)
,
12)
.
13)
,
14)
,
15)
,
16)
.
Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв’язуються розкладанням їхньої лівої частини на множники.
Приклад 1.
Розв’язати
рівняння
.
Розв’язання
Врахувавши, що
, матимемо:
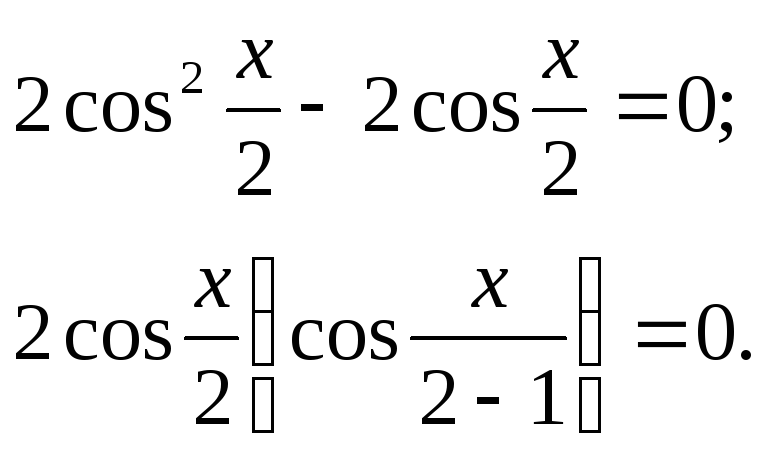
Добуток дорівнює нулю, якщо хоча б один із множників дорівнює нулю. Тому:
1)
.
2)
.
Відповідь:
.
Приклад 2.
Розв’язати
рівняння
.
Розв’язання
;
.
1)
.
2)
.
Відповідь:
.
60. Розв’язати рівняння:
1)
,
2)
,
3)
,
4)
,
5)
,
6)
,
7)
,
8)
,
9)
,
10)
,
11)
,
12)
,
13)
,
14)
,
15)
,
16)
.
Рівняння виду
,
де
і
не дорівнюють нулю, називається однорідним
рівнянням 1-го степеня.
Значення
,
при яких
дорівнює нулю, не задовольняє даному
рівнянню, бо тоді і
теж дорівнював би нулю. Тому можна
розділити обидві частини рівняння на
.
Маємо:
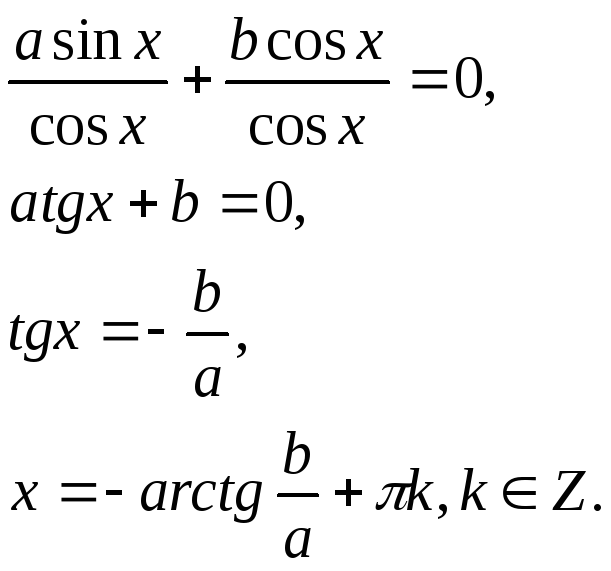
Рівняння виду:
називається однорідним рівнянням 2-го
степеня.
Якщо числа
не дорівнюють нулю, то розділимо дане
рівняння на
(або на
).
У даному рівнянні
,
бо в супротивному випадку
теж дорівнював би нулю. Тоді
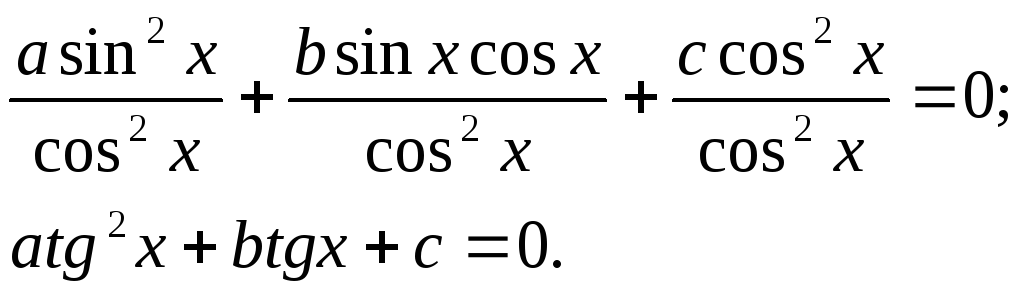
61. Розв’язати рівняння:
1)
,
2)
,
3)
,
4)
,
5)
,
6)
,
7)
,
8)
9)
,
10)
,
11)
,
12)
,
13)
,
14)
.
62. Розв’язати рівняння
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
.