§7 Властивості та графіки тригонометричних функцій Властивості і графік функції

1. Область визначення – уся числова пряма, тобто ;

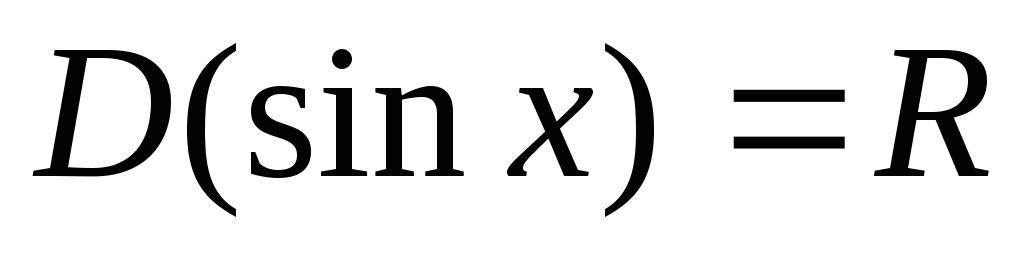2. Область значень – відрізок 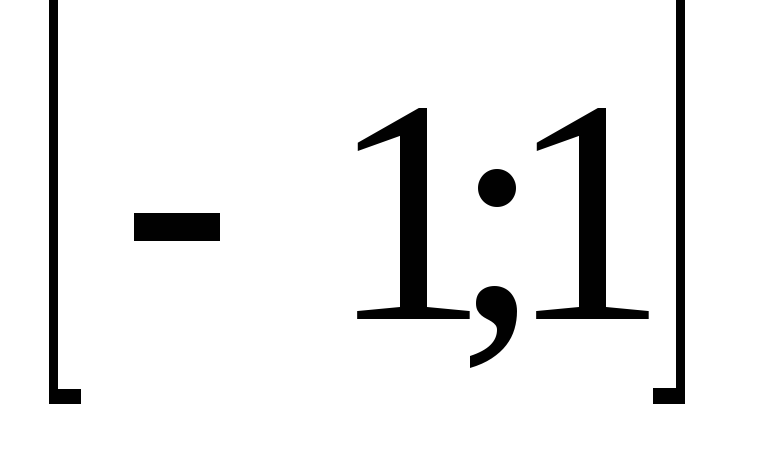, тобто ;

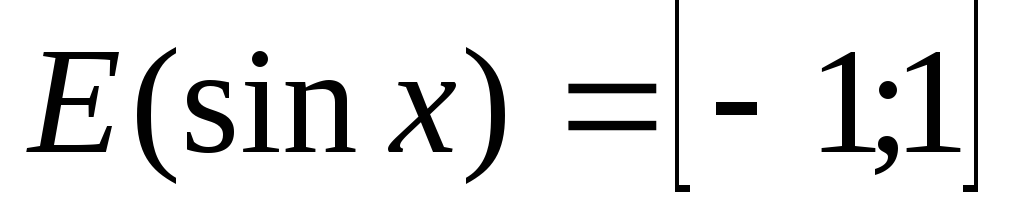3. Функція 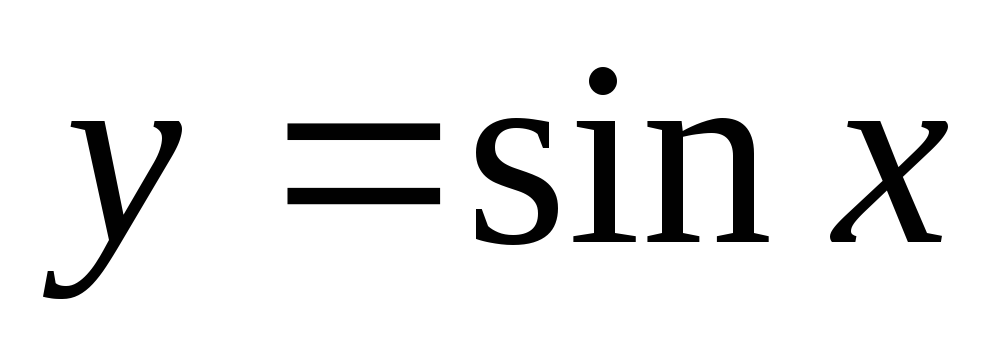– непарна, тобто 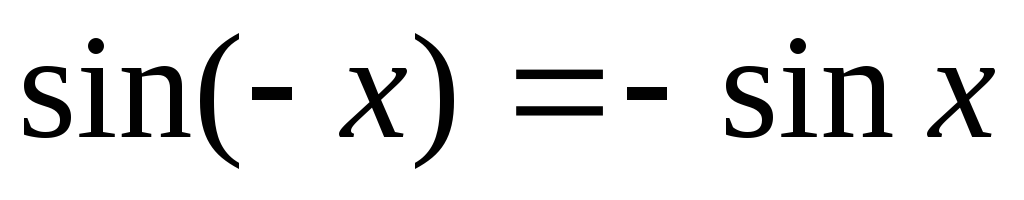; графік симетричний відносно початку координат;

4. Функція періодична з основним періодом ;

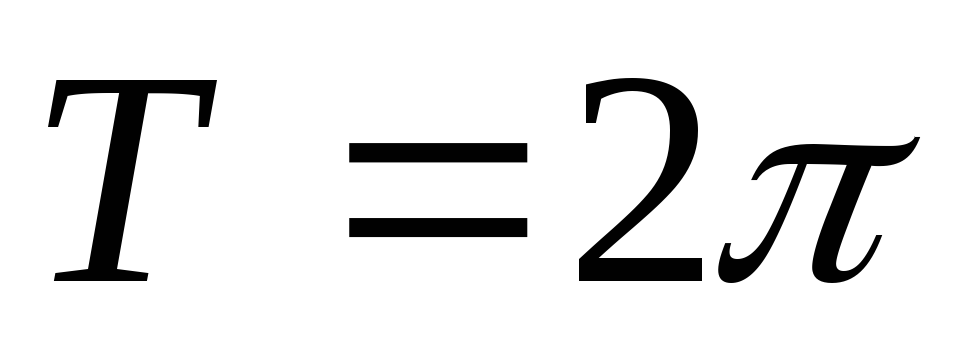5. Нулі функції: 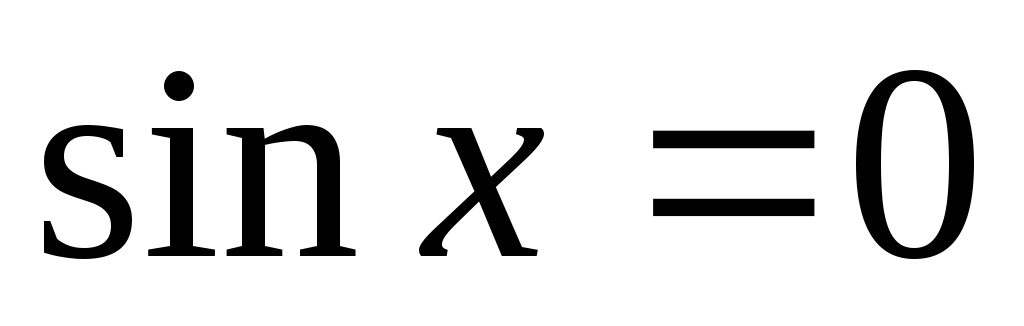при , ;

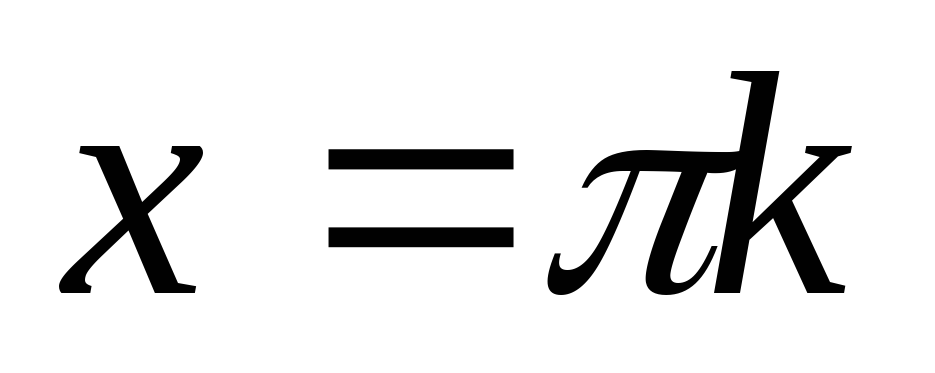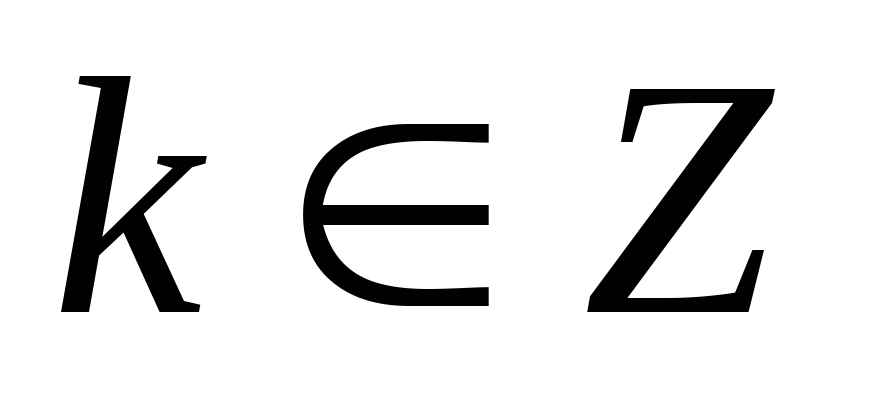6. Інтервали знакосталості:

А) , якщо , ;

Б) , якщо , ;

7. Інтервали зростання й спадання:

А) Функція зростає на проміжках , ;

Б) Функція спадає на проміжках , ;

8. Екстремуми функції:

А) при , ;

Б) при , ;

9. Функція 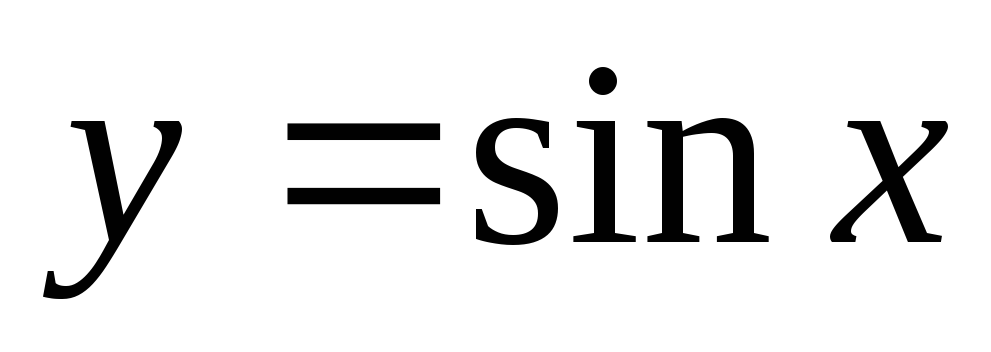є обмеженою, .

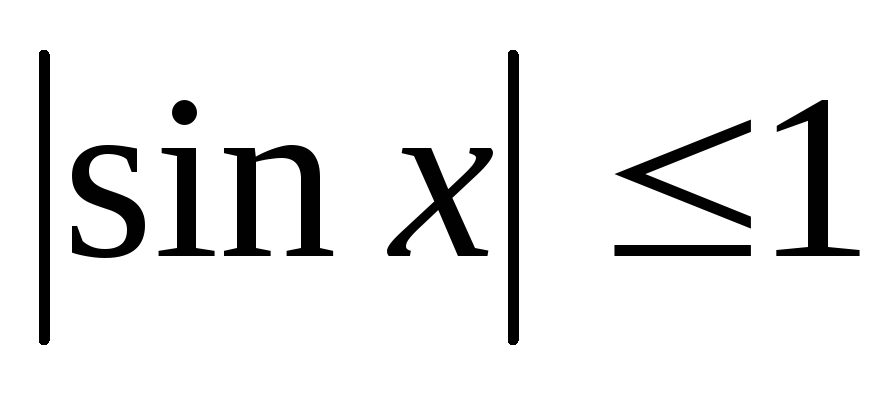Графік функції називається синусоїдою, він показаний на р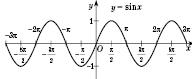ис. 2.

Рис. 2

Властивості і графік функції

1. Область визначення – уся числова пряма, тобто ;

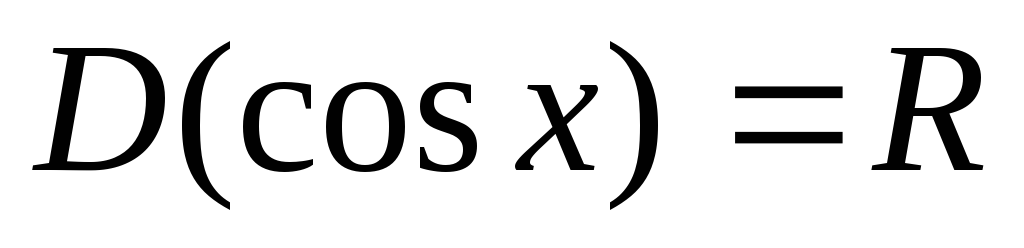2. Область значень – відрізок 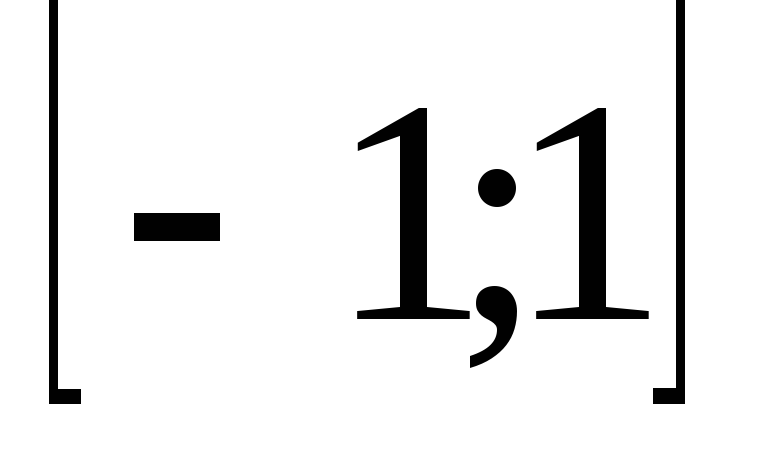, тобто ;

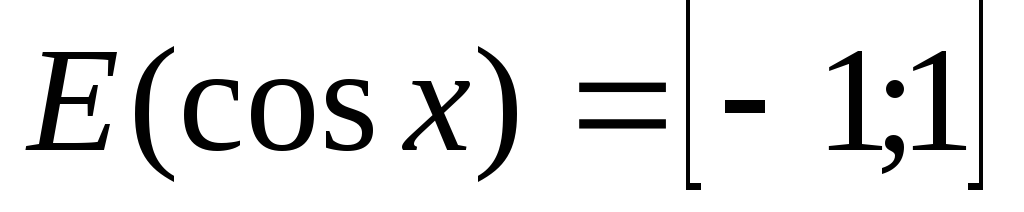3. Функція 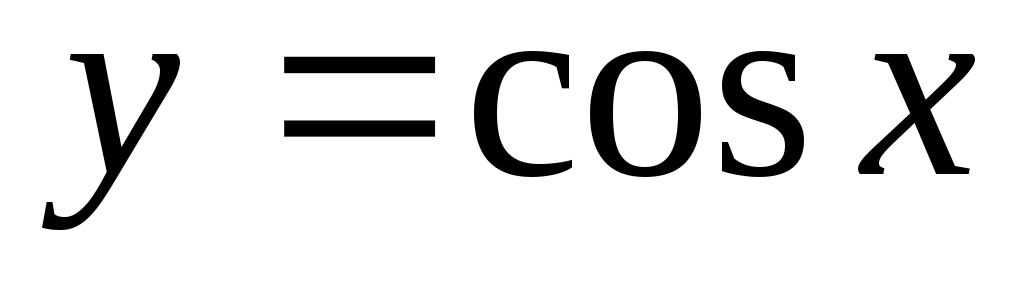– парна, тобто 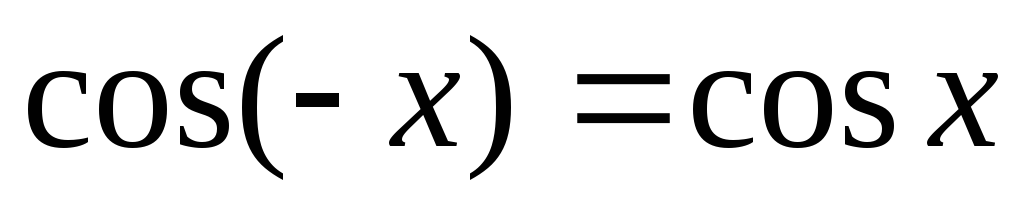; графік симетричний щодо осі Оу;

4. Функція періодична з основним періодом ;

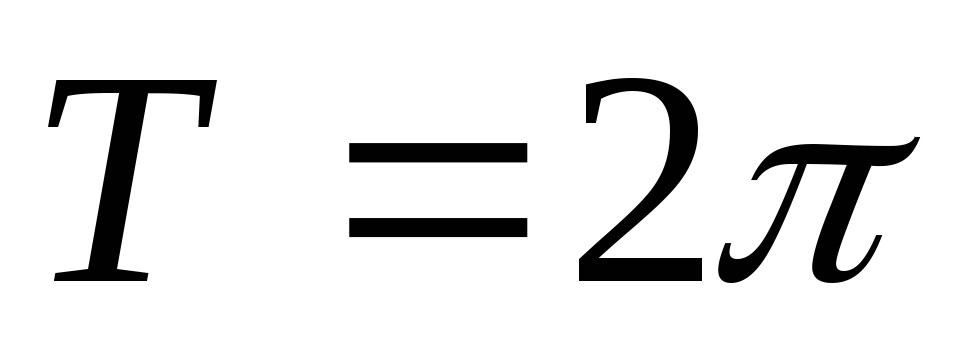5. Нулі функції: 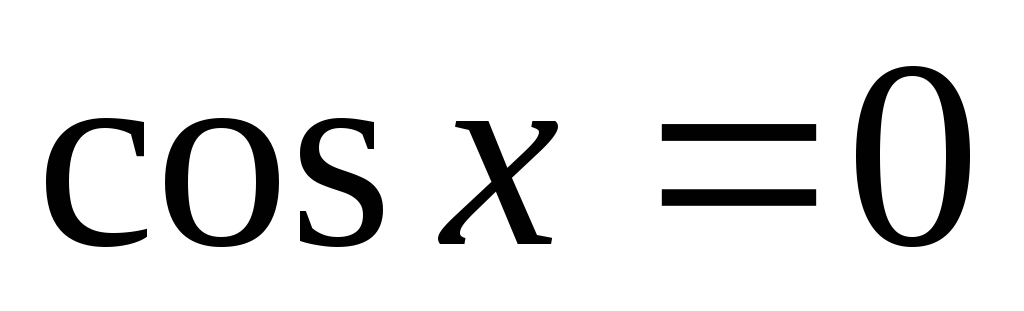при , ;

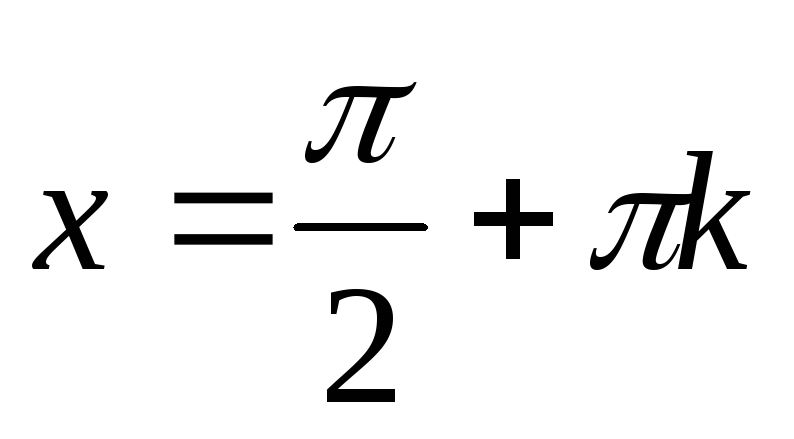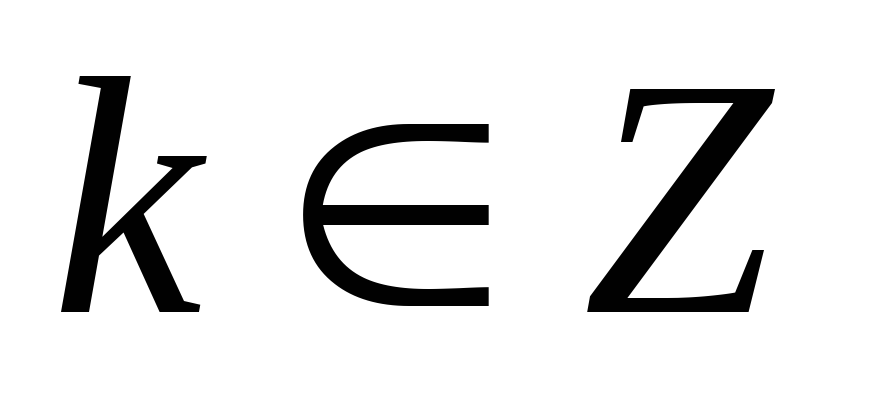6. Інтервали знакосталості:

А) , якщо , ;

Б) , якщо , ;

7. Інтервали зростання і спадання:

А) Функція зростає на проміжках , ;

Б) Функція спадає на проміжках , ;

8. Екстремуми функції:

А) при , ;Б) при , ;

9. Функція 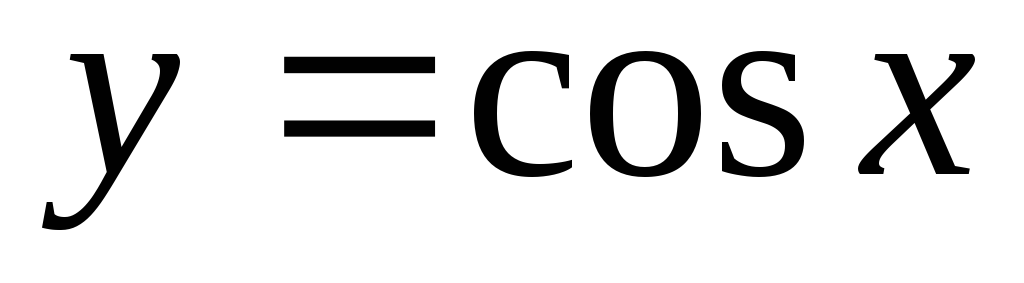є обмеженою, .

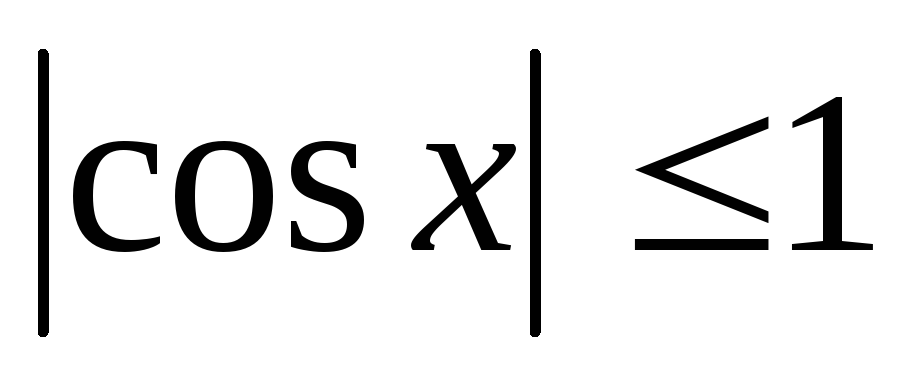Графік функції називається косинусоїдою, він показаний на р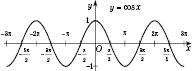ис. 3.

Рис. 3

Властивості і графік функції

1. Область визначення – множина усіх дійсних чисел, крім чисел виду 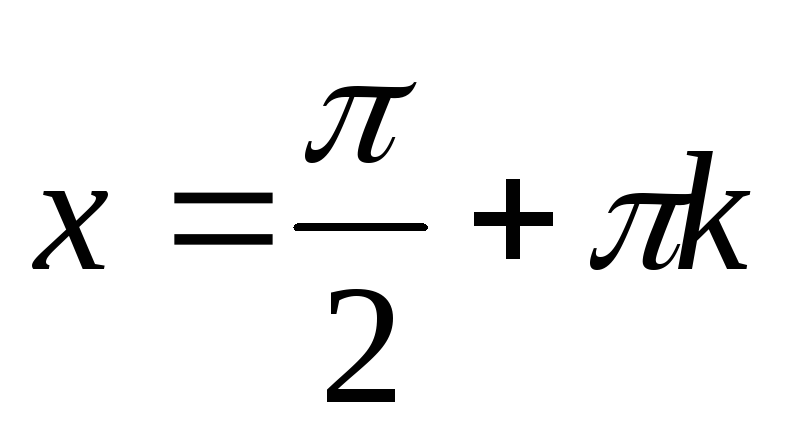, , 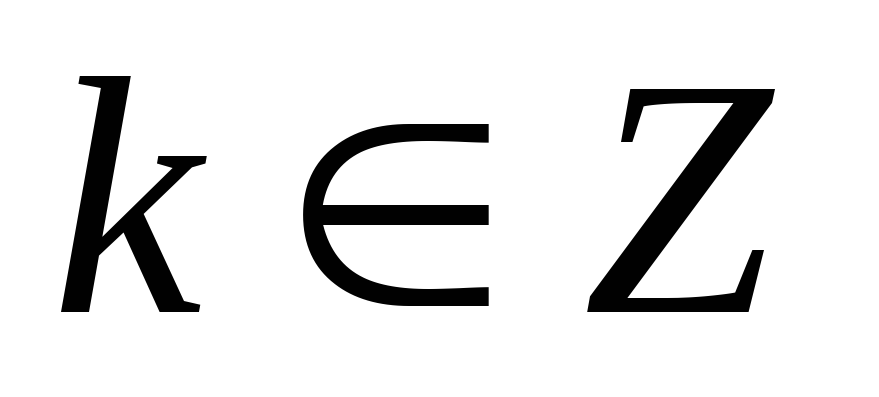тобто , ;

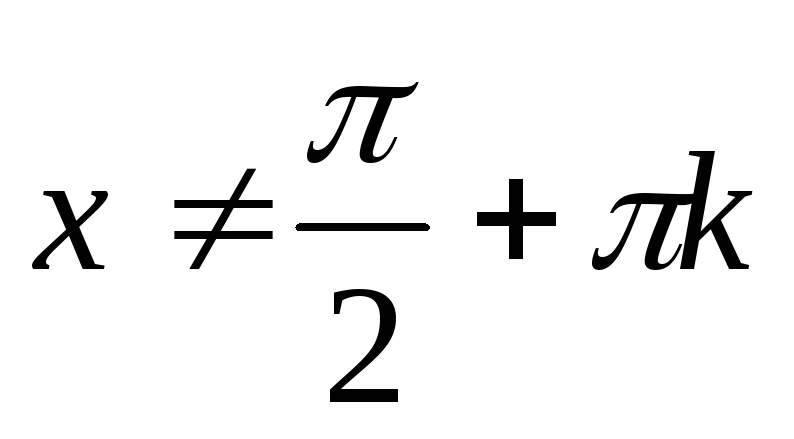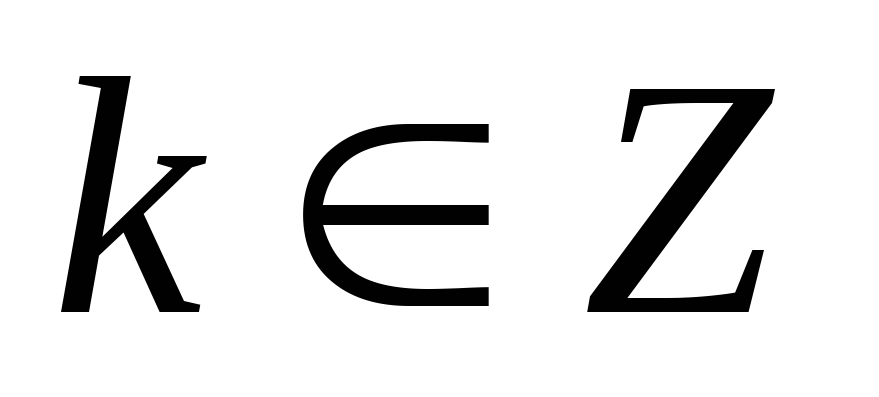2. Область значення – вся числова пряма, тобто ;

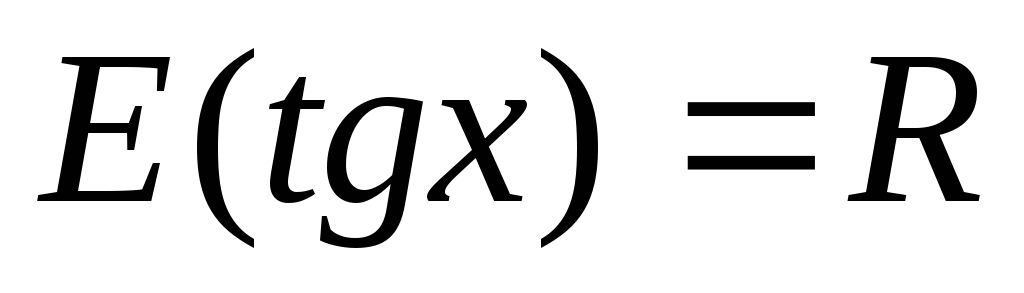3. Функція 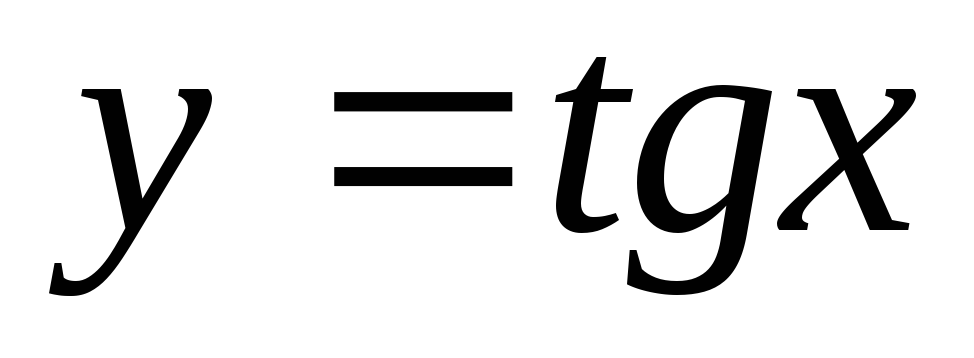– непарна, тобто 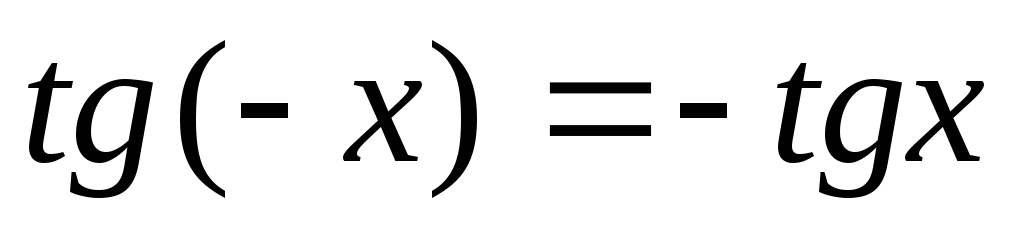, графік симетричний відносно початку координат;

4. Функція періодична з основним періодом ;

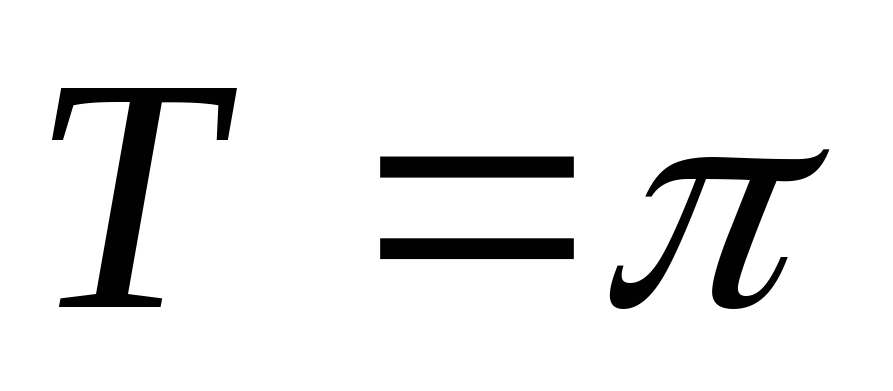5. Нулі функції 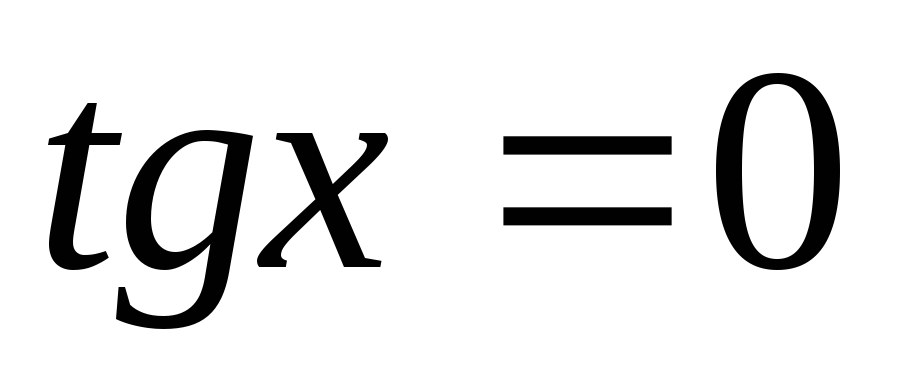при , ;

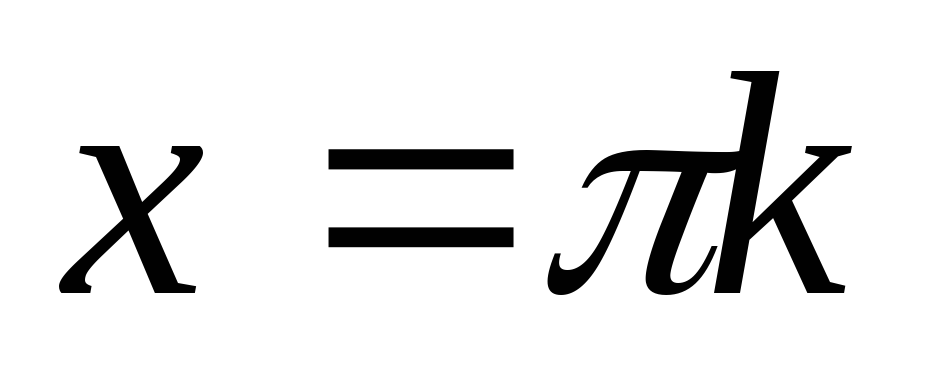6. Інтервали знакосталості:

А) , якщо , ;

Б) , якщо , ;

7. Інтервали зростання і спадання: функція 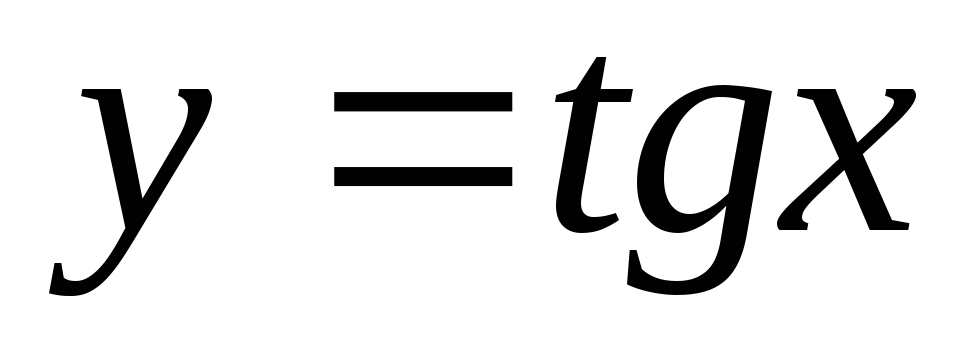зростає на проміжках , ;

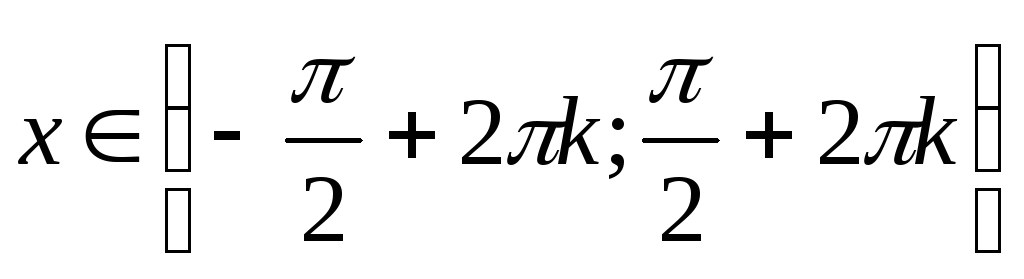8. Функція 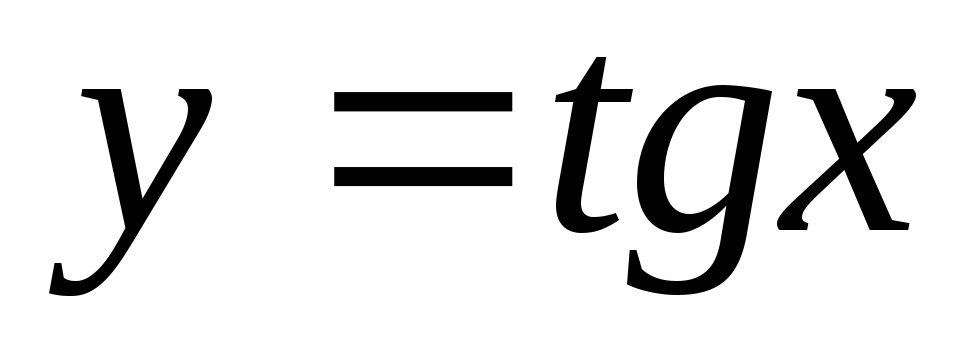екстремумів не має;

9. Функція 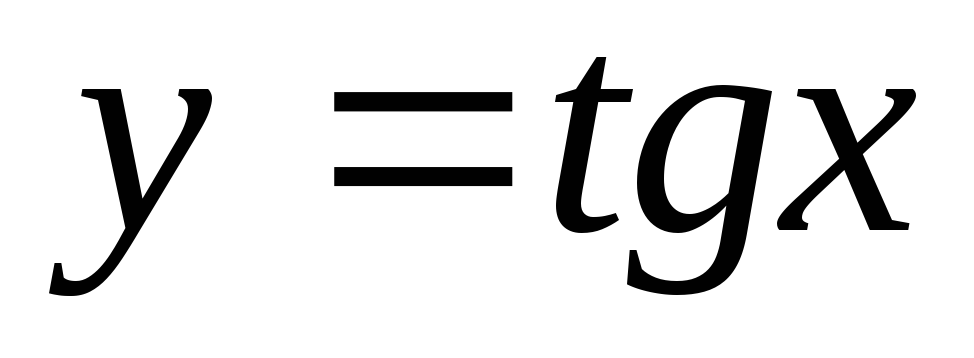не обмежена.

Графік функції називається тангенсоїдою, він показаний на рис. 4.

Прямі , називаються вертикальними асимптотами графіка функції

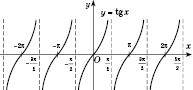Рис. 4

Властивості та графік функції

1. Область визначення – множина усіх дійсних чисел, крім чисел виду 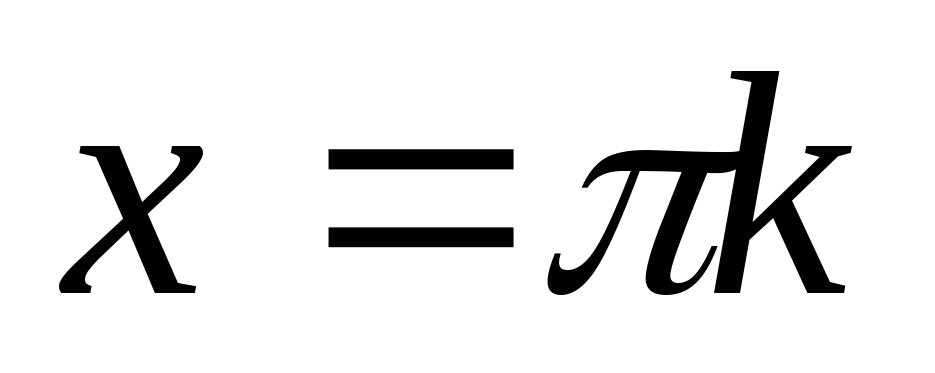, , 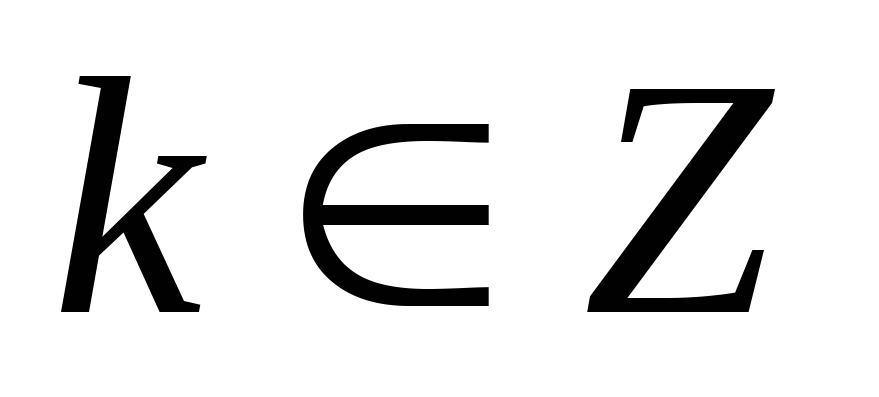тобто , ;

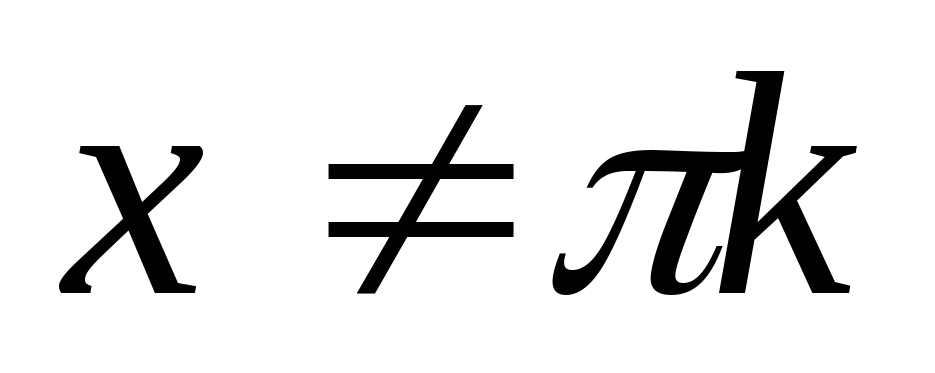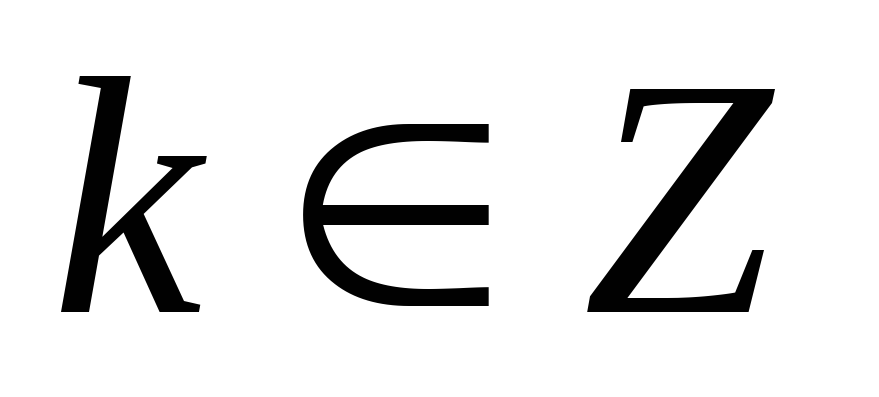2. Область значень – вся числова пряма, тобто ;

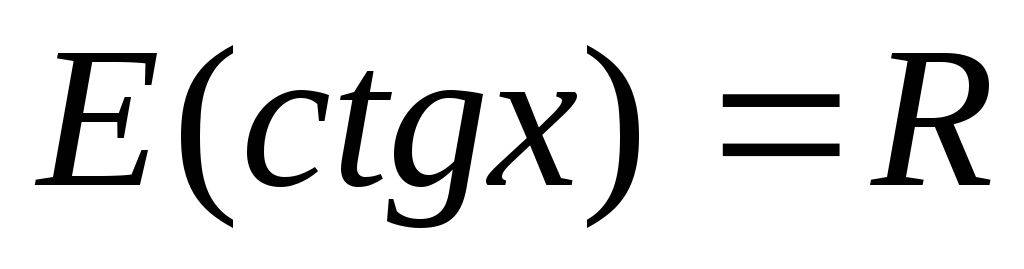3. Функція 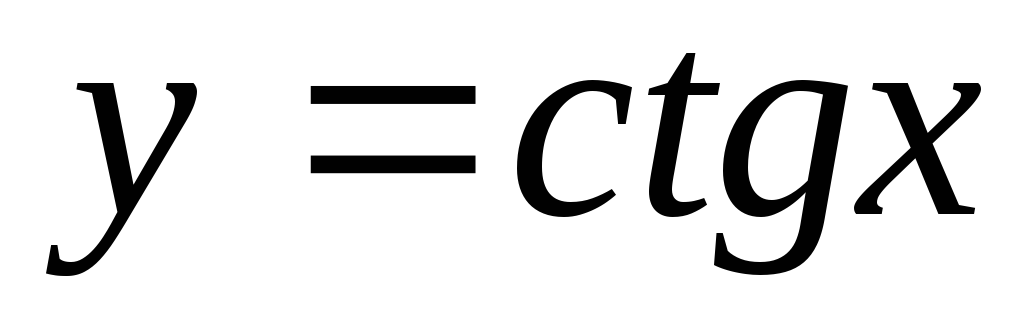– непарна, тобто 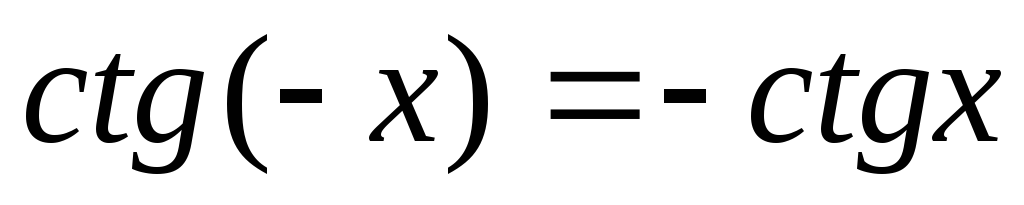, графік симетричний відносно початку координат;

4. Функція періодична з основним періодом ;

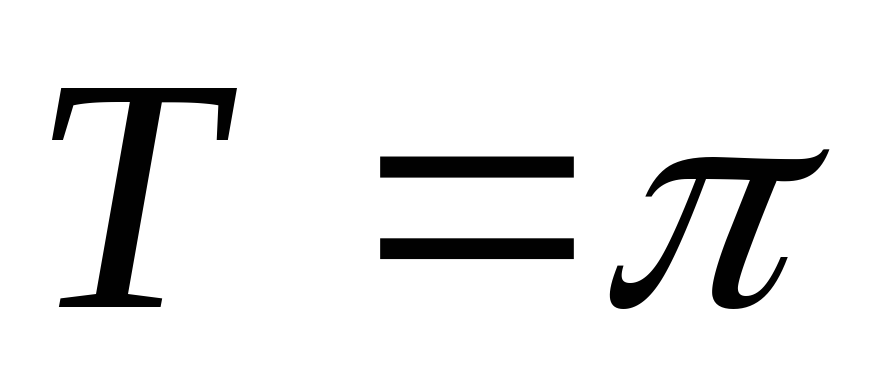5. Нулі функції: 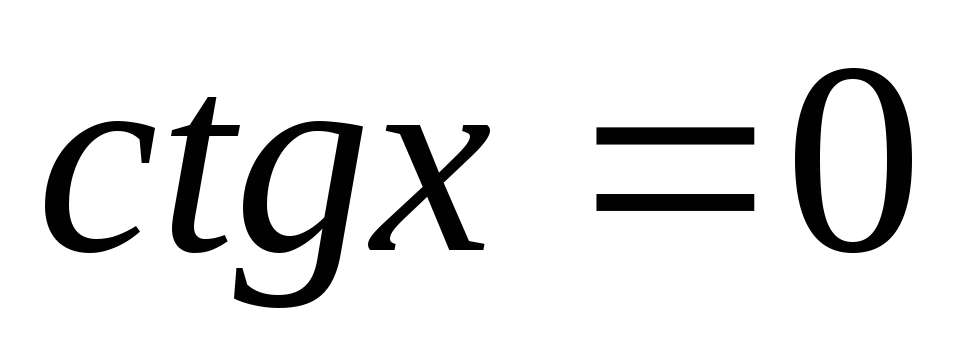при , ;

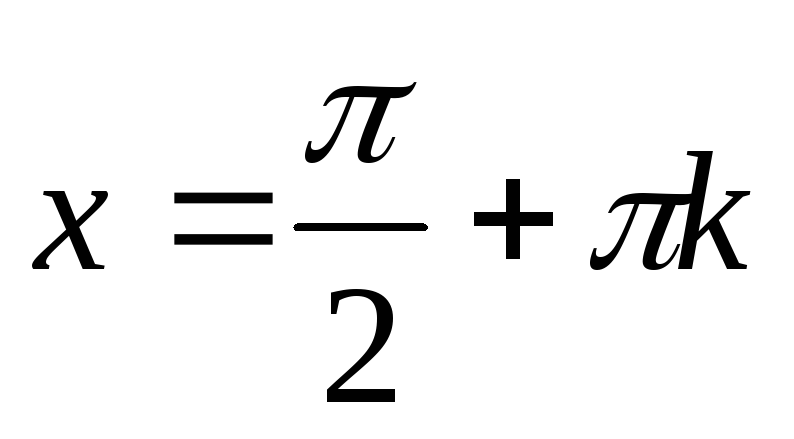6. Інтервали знакосталості:

А) , якщо , ;

Б) , якщо , ;

7. Інтервали зростання і спадання : функція 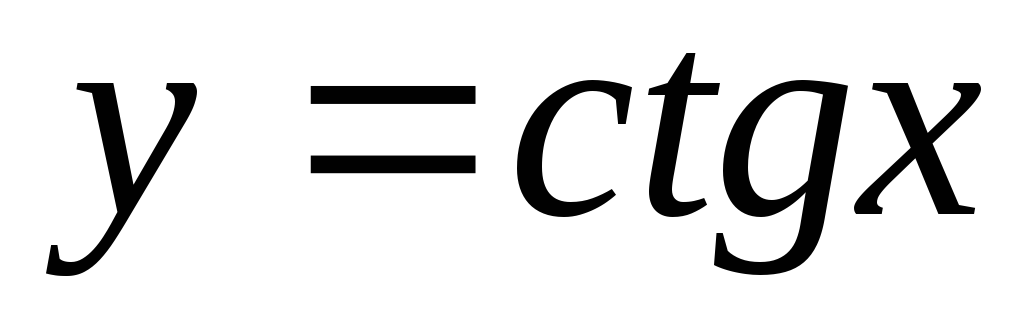спадає на проміжках , ;

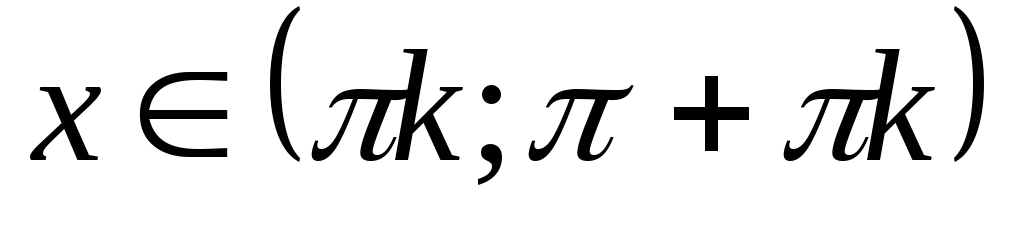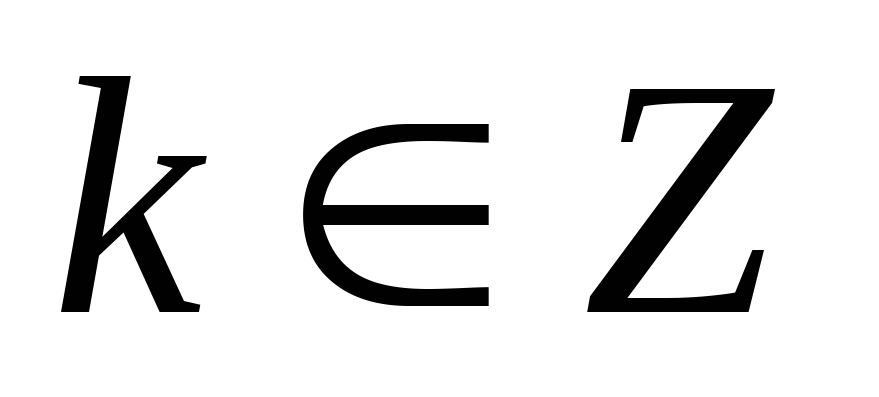8. Функція 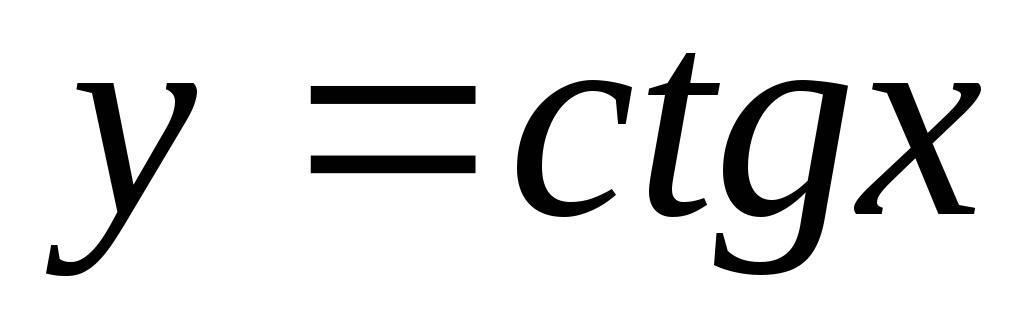екстремумів не має;

9. Функція 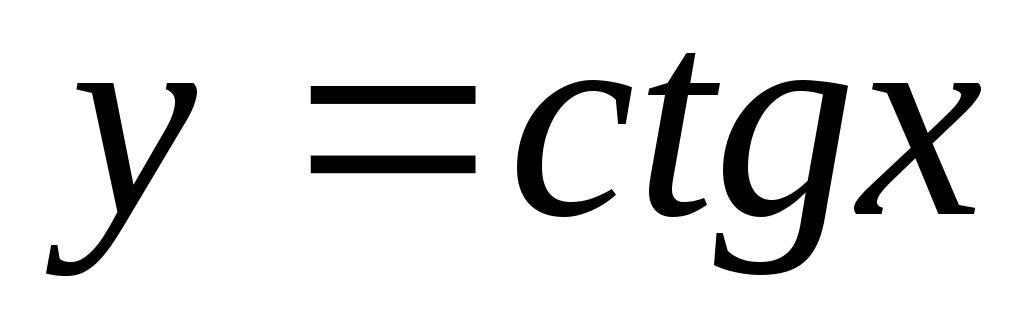необмежена.

Графік функції називається котангенсоїдою, він показаний на рис. 5. Прямі , називаються вертикальними асимптотами графіка функції .

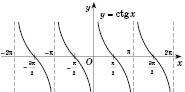Рис. 5

42. Побудувати графіки функцій:

1) ; 2) ;

3) ; 4) ;

5) ; 6) ;

7) ; 8) ;

9) ; 10) ;

11) ; 12) .

43. Використовуючи властивості функцій порівняти числа:

1) і ; 2) і ;

3) і ; 4) і ;

5) і ; 6) і ;

7) і ; 8) і ;

9) і ; 10) і ;

11) і ; 12) і .

44. Розташувати числа у порядку зростання:

1) ; 2) ;

3) ; 4) ;

5) ; 6) ;

7) ; 8) ;

45. Побудувати графік функції на проміжку та знайти:

1) значення , якщо ;

2) значення , якщо ;

3) проміжок, де функція спадає.

46. Побудувати графік функції на проміжку та знайти:

1) значення , якщо ;

2) значення , якщо ;

3) проміжок, на якому функція зростає.

47. Побудувати графік функції на проміжку та знайти:

1) значення , якщо ;

2) значення , якщо ;

3) проміжок, на якому функція спадає.

48. Побудувати графік функції на проміжку та знайти:

1) значення , якщо ;

2) значення , якщо ;

3) проміжок, на якому функція зростає.

49. Побудувати графіки функцій:

1) ; 2) ;

3) ; 4) ;

5) ; 6) ;

7) ; 8) .