
- •Алгебра та початки аналізу Частина іі
- •Харків 2011 Передмова
- •Розділ 1 Тригонометричні функції числового аргументу
- •§1 Радіанна міра вимірювання кутів
- •§2 Тригонометричні функції числового аргументу
- •§3 Властивості тригонометричних функцій
- •§4 Основні тригонометричні тотожності
- •§5 Формули зведення
- •§6 Основні формули тригонометрії
- •§7 Властивості та графіки тригонометричних функцій Властивості і графік функції
- •Властивості і графік функції
- •Властивості і графік функції
- •Властивості та графік функції
- •§8 Обернені тригонометричні функції
- •§9 Розв’язання найпростіших тригонометричних рівнянь
- •§ 10 Розв’язання тригонометричних рівнянь
- •§ 11 Розв’язання тригонометричних нерівностей
- •Розділ 2 Похідна функції та її застосування
- •§ 12 Приріст функції в точці. Похідна функції та її механічний зміст
- •§ 13 Похідна степеневої функції
- •§14 Похідна суми, різниці, добутку та частки двох функцій Правила диференціювання
- •§15 Похідна складеної функції
- •§ 16 Похідні тригонометричних функцій
- •§ 17 Похідна показникової функції
- •§ 18 Похідна логарифмічної функції
- •§ 19 Геометричний зміст похідної
- •§ 20 Похідні вищих порядків
- •§ 21 Диференціал функції і його застосування до наближених обчислень
- •§ 22 Ознака сталості, зростання та спадання функції.
- •§ 23 Екстремум функції
- •§ 24 Побудова графіків функцій Загальна схема для побудови графіків функцій
- •§ 25 Найменше та найбільше значення функції
- •Розділ 3 Інтеграл та його застосування
- •§ 26 Первісна функції. Невизначений інтеграл та його властивості
- •Основні властивості невизначених інтегралів
- •Основні формули інтегрування
- •§ 27 Визначений інтеграл та його властивості
- •Основні властивості визначеного інтегралу:
- •§ 28 Площа криволінійної трапеції
- •§ 29 Застосування визначеного інтеграла при розв’язанні фізичних задач
- •Розділ 4 Елементи теорії ймовірностей і математичної статистики
- •§ 30 Елементи комбінаторики
§5 Формули зведення
Формулами
зведення називаються
співвідношення, за допомогою яких
значення тригонометричних функцій
аргументів
![]() ,
,
![]() ,
,
![]() ,
,
![]() виражаються через значення
виражаються через значення
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
При застосування формул зведення можна користуватися такими правилами:
1) якщо у формулах
містяться кути
![]() і
і
![]() ,
то назва функції не змінюється; якщо ж
у формулах містяться кути
,
то назва функції не змінюється; якщо ж
у формулах містяться кути
![]() і
і
![]() ,
то назва функції змінюється на подібну
(синус – на косину, тангенс – на котангенс
і навпаки);
,
то назва функції змінюється на подібну
(синус – на косину, тангенс – на котангенс
і навпаки);
2) щоб визначити
знак у правій частині формули («+», або
«-»), досить, вважаючи кут
![]() гострим,
визначити
знак виразу, який стоїть у лівій частині
формули; при цьому перед функцією кута
гострим,
визначити
знак виразу, який стоїть у лівій частині
формули; при цьому перед функцією кута
![]() ставлять такий знак, який має зведена
функція кутів
ставлять такий знак, який має зведена
функція кутів
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Наприклад,
![]() ;
;
![]() .
.
27. Звести
до тригонометричних функцій кута
![]() :
:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
28. Звести до тригонометричних функцій кутів першої чверті:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
![]() ;
;
13)
![]() ;
14)
;
14)
![]() ;
;
15)
![]() ;
16)
;
16)
![]() ;
;
17)
![]() ;
18)
;
18)
![]() ;
;
19)
![]() ;
20)
;
20)
![]() ;
;
21)
![]() ;
22)
;
22)
![]() ;
;
23)
![]() ;
24)
;
24)
![]() .
.
29. Обчислити:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
![]() ;
;
13)
![]() ;
14)
;
14)
![]() ;
;
30. Знайти значення виразу:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() .
.
31. Спростити вирази:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
 ;
;
6)
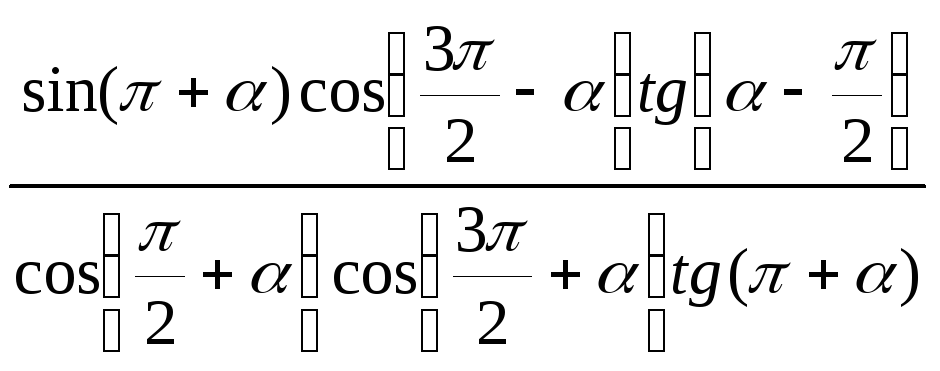 ;
;
7)
![]() ;
;
8)
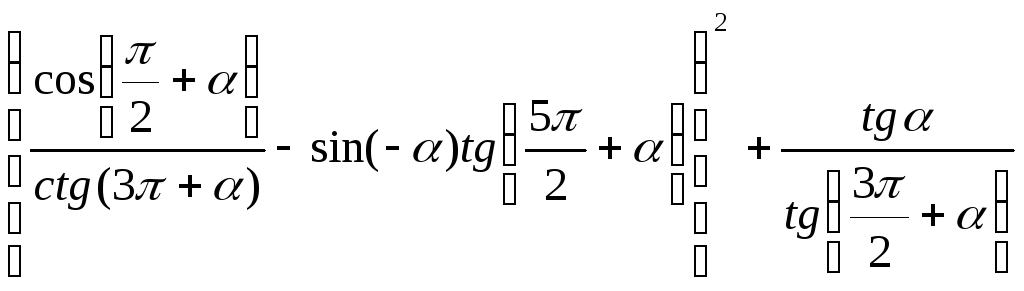 .
.
32*. Довести тотожність:
1)
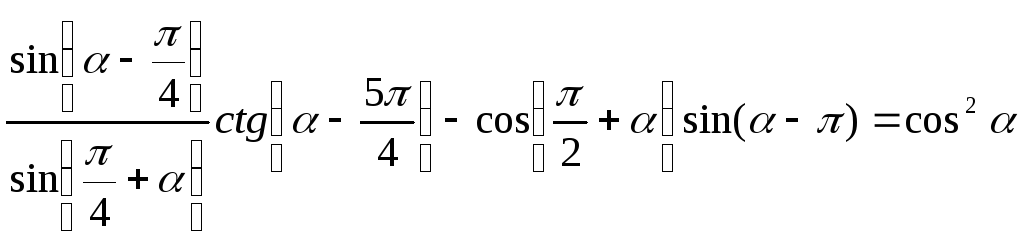 ;
;
2)
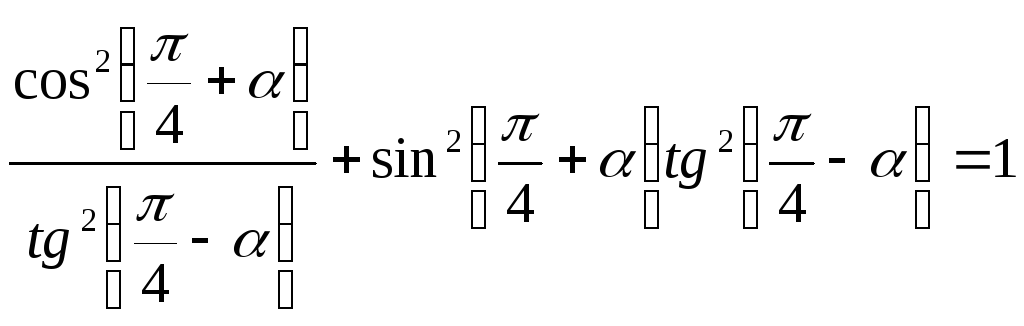 .
.
§6 Основні формули тригонометрії
Можна виділити основні групи тригонометричних формул.
1. Основні співвідношення між тригонометричними функціями того самого аргументу (див. §4).
2. Формули додавання аргументів:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
3. Формули подвійного і потрійного аргументів:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
4. Формули зниження степеня:
![]() ;
;
![]() .
.
5. Формули перетворення добутку тригонометричних функцій у суму
![]() ;
;
![]() ;
;
![]() .
.
6. Формули перетворення суми і різниці однойменних тригонометричних функцій у добуток:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
7. Формули тригонометричних функцій половинного аргументу:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
33. Спростити вирази:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
![]() ;
;
13)
![]() ;
14)
;
14)
![]() ;
;
15)
![]() ;
16)
;
16)
![]() ;
;
17)
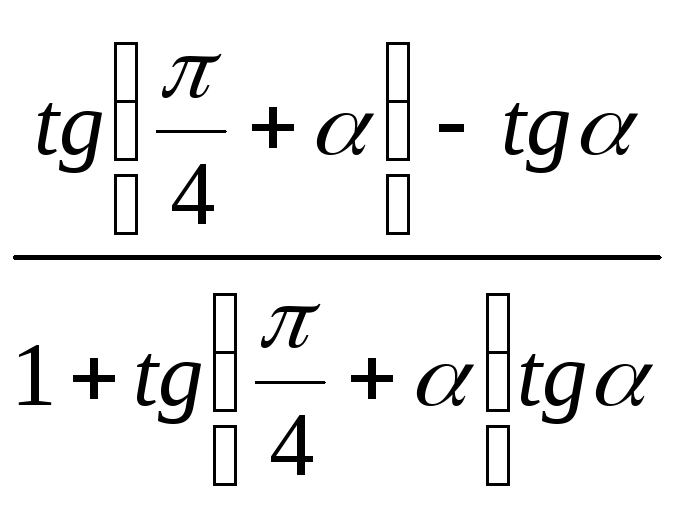 ;
18)
;
18)
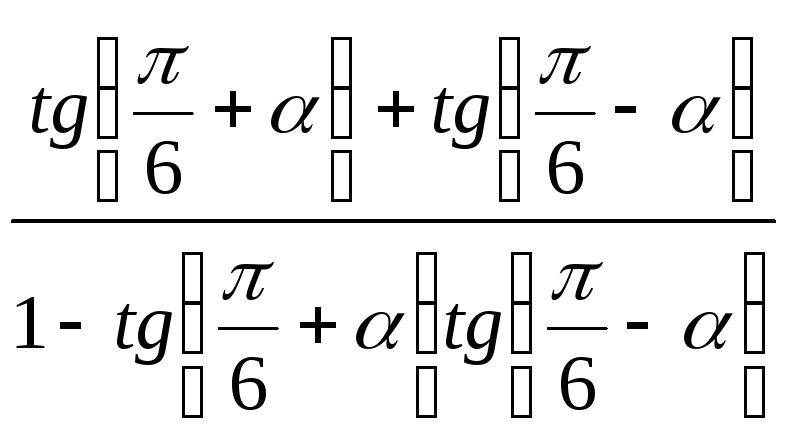 .
.
34. Довести тотожність:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() .
.
35. Знайти:
1)
![]() ;
2)
;
2)
![]() ;
;
2)
![]() ;
4)
;
4)
![]() ;
;
3)
![]() ;
6)
;
6)
![]() .
.
36.
![]() .
Знайти
.
Знайти
![]() .
.
37.
![]() .
Знайти
.
Знайти
![]() .
.
38. Знайти значення виразу:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
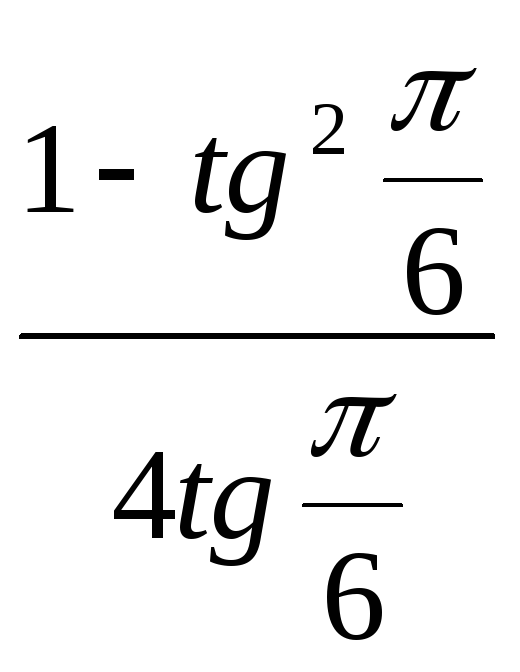 .
.
39. Спростити вирази:
1)
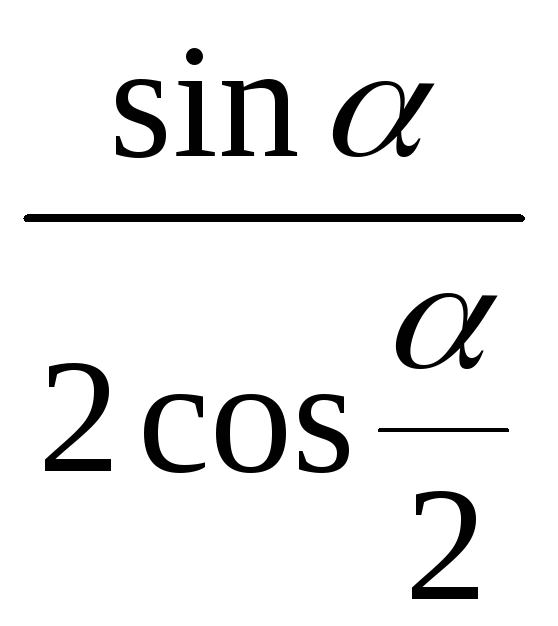 ;
2)
;
2)
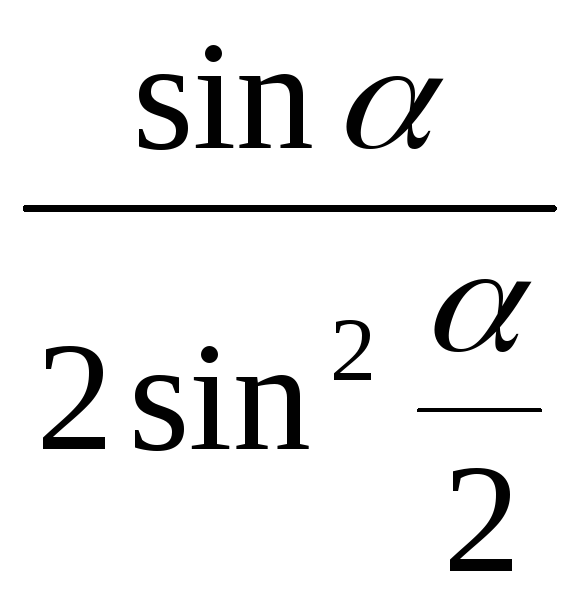 ;
;
3)
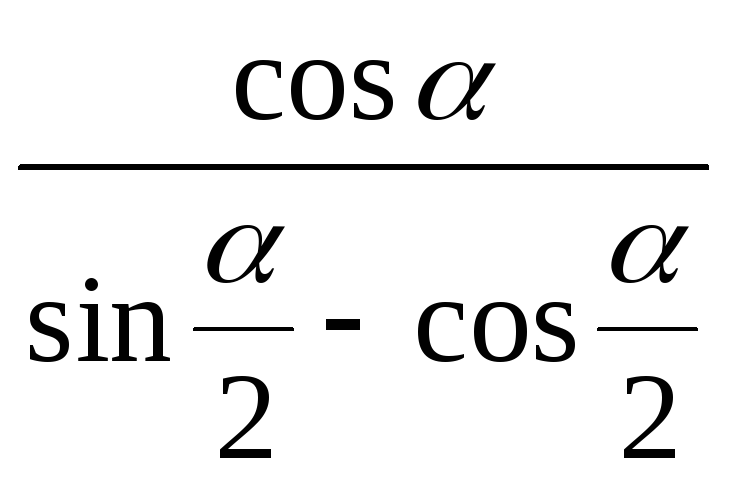 ;
4)
;
4)
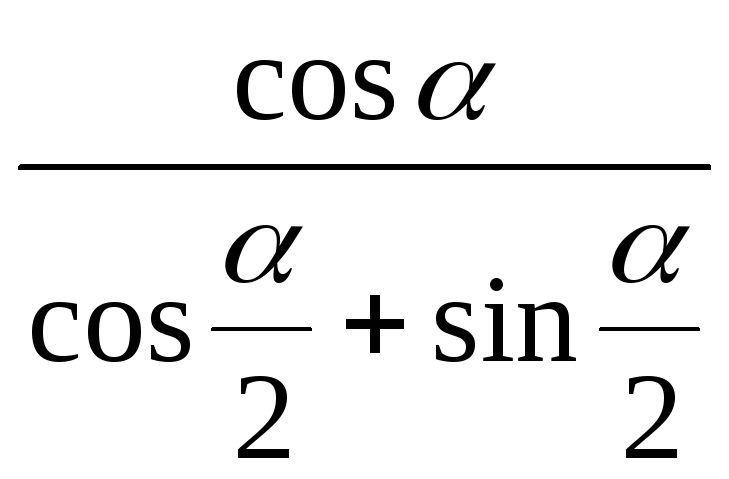 ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
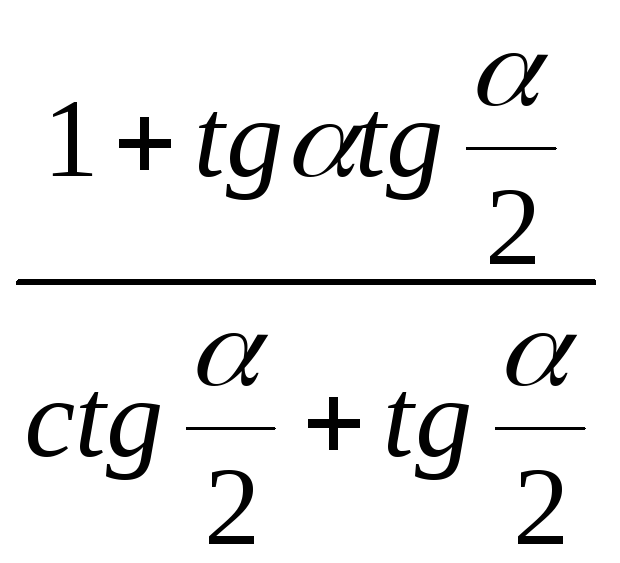 ;
;
13)
![]() ;
14)
;
14)
![]() ;
;
15)
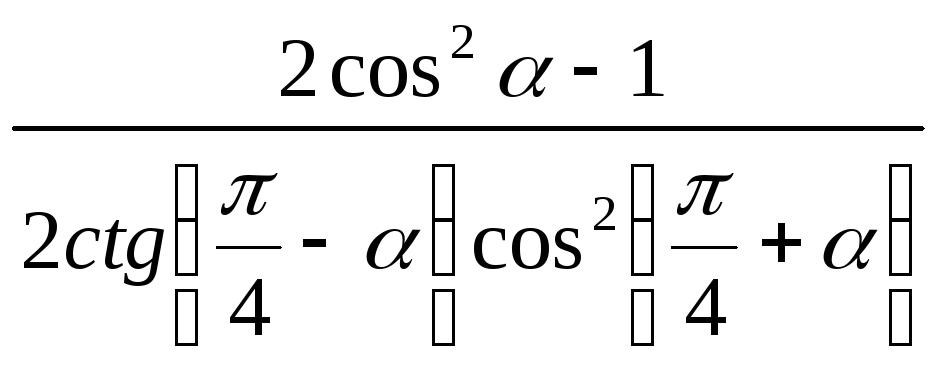 ;
16)
;
16)
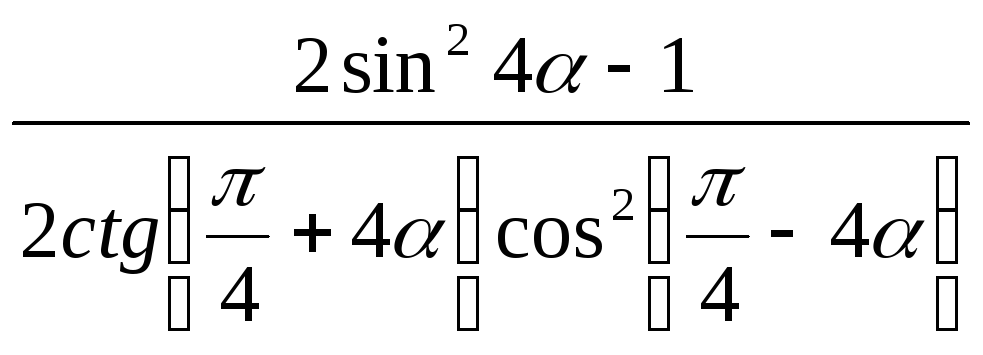 .
.
40. Перетворити на добуток:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
![]() ;
;
13)
![]() ;
14)
;
14)
![]() ;
;
15)
![]() ;
16)
;
16)
![]() ;
;
17)
![]() ;
18)
;
18)
![]() ;
;
19)
![]() ;
20)
;
20)
![]() .
.
41. Довести тотожність:
1)
![]() ;
;
2)![]() ;
;
3)
![]() ;
;
4)
![]() .
.
